Qu’est-ce que le MRUA?
Un MRUA est un Mouvement Rectiligne Uniformément Accéléré. Il s’agit donc d’un mouvement qui se déroule:
- de façon rectiligne: càd en ligne droite \(\Rightarrow\) le vecteur vitesse \(\overrightarrow{v}\) ne peut donc pas changer de direction
- de façon uniformément accélérée \(\Rightarrow\) le vecteur accélération \(\overrightarrow{a}\) est constant: il ne peut donc ni changer de direction, ni d’intensité
MRUA avec vitesse et accélération positives
C’est le premier cas de figure possible, les vecteurs vitesse \(\overrightarrow{v}\) et accélération \(\overrightarrow{a}\) sont orientés dans le sens du référentiel. Ils ont donc, des composantes scalaires \(v\) et \(a\) positives.
Le diagramme d’un tel mouvement ressemble à ceci:

Dans cet exemple, le vecteur accélération (représenté en vis-à-vis du vecteur vitesse pour plus de lisibilité) est bien un vecteur constant de composante scalaire égale à \(1\Big[\frac{m}{s²}\Big]\). Qu’est-ce que cela veut dire? Reprenons la définition de la notion d’accélération:
\begin{equation}
\overrightarrow{a}=\frac{\Delta\overrightarrow{v}}{\Delta t}
\tag{1}
\end{equation}
Etant donné que \(\Delta t\) est un scalaire positif, les vecteurs \(\overrightarrow{a}\) et \(\Delta\overrightarrow{v}\) ont nécessairement même direction et la relation \((1)\) peut s’écrire sous sa forme scalaire:
\begin{equation}
a = \frac{\Delta v}{\Delta t} \tag{2}
\end{equation}
On peut introduire dans \((2)\) la valeur \(a=1m/s²\). On obtient:
\begin{align}
1\bigg[\frac{m}{s²}\bigg] &= \frac{\Delta v}{\Delta t} \\
\end{align}
Pour \(\Delta t = 1s\)
\begin{align}
1\bigg[\frac{m}{s²}\bigg] &= \frac{\Delta v}{1[s]} \\
\Delta v &= 1\bigg[\frac{m}{s²}\bigg] .1[s] \\
\Delta v &= 1\bigg[\frac{m}{s}\bigg] \\
\end{align}
En français svp? 😯 A chaque intervalle de temps de 1\(s\), la variation de vitesse sera de \(+ 1m/s\). Autrement dit, la valeur du vecteur vitesse va augmenter de \(1m/s\) toutes les secondes. C’est bien ce que montre la Fig.1. A chaque temps chrono \(t_{0}, t_{1} …\), la valeur du vecteur vitesse (tracé en orange et enfoncé dans le capot avant de la voiture) augmente de \(1 m/s\).
On remarquera encore sur cette figure que, étant donné que la valeur de la vitesse augmente, à chaque seconde qui s’écoule, l’espace parcouru est de plus en plus grand \(1,5m; \, 2,5m \, et \, 3,5m\). On quantifiera tout cela dans l’approche algébrique du MRUA.
Vérifions juste que le vecteur accélération \(\overrightarrow{a}\) est bien cohérent avec les vecteurs vitesse \(\overrightarrow{v}\) via une petite construction géométrique (Fig.2.):

Si au bout du vecteur \({\overrightarrow{v}_{3}}\), on ajoute le vecteur \(-{\overrightarrow{v}_{1}}\), on obtient le vecteur \(\Delta{\v{v}_{2}}\). Mathématiquement, cette relation s’écrit:
\begin{equation}
\Delta{\overrightarrow{v}_{2}} = {\overrightarrow{v}_{3}} – {\overrightarrow{v}_{1}} \tag{3}
\end{equation}
Etant donné que les 3 vecteurs ont la même direction (horizontale), on peut réécrire la relation \((3)\) sous sa forme scalaire:
\begin{equation}
\Delta{v_{2}} = {v_{3}} – {v_{1}} \Leftrightarrow \Delta{v_{2}} = 4 – 2 = + 2 \big[\frac{m}{s}\big] \tag{4}
\end{equation}
La relation \((1)\) nous montre que le vecteur \(\overrightarrow{a}\) est relié au vecteur \(\Delta\overrightarrow{v}\) par un scalaire positif \((\Delta t)\), les deux vecteurs ont donc nécessairement la même direction (ils sont reliés par un scalaire) et le même sens (ce scalaire est positif), ce qui a deux conséquences:
- Le vecteur \(\overrightarrow{a}\) est un vecteur horizontal et orienté vers la droite, comme le vecteur \(\Delta\overrightarrow{v}\)
- La relation \((1)\) peut s’écrire sous sa forme scalaire et la relation \((2)\) est donc toujours valable. Cela nous conduit à la valeur du vecteur \(\overrightarrow{a}\): \(\, a= +2/+2 = +1 [m/s²]\) puisque la variation de vitesse de part et d’autre du point 2 \(\big(\Delta{\overrightarrow{v}_{2}}\big)\) a lieu entre les instants \(t_{1}\) et \(t_{3}\) càd en 2 secondes.
Je retiens…
Si le vecteur accélération (positif) est parallèle et de même sens que le vecteur vitesse (positif), la valeur de la vitesse augmente régulièrement au cours du temps.
MRUA avec vitesse positive et accélération négative
C’est le deuxième cas de figure, le vecteur vitesse \(\overrightarrow{v}\) est dans le sens du référentiel (parce que le mouvement se fait dans ce sens) mais le vecteur accélération \(\overrightarrow{a}\) est orienté dans le sens opposé au référentiel. La composante scalaire de la vitesse \(v\) est donc positive tandis que celle de l’accélération, \(a\), est négative.
Le diagramme d’un tel mouvement ressemble à ceci:

En faisant le même raisonnement que précédemment, on introduira la valeur \(a=-1m/s²\) dans l’expression \((2)\) . On en déduira donc que, pour chaque seconde de mouvement, la valeur du vecteur vitesse diminue de \(1m/s\), ce qui est conforme à la Fig.3.
La voiture avance donc de moins en moins vite et parcourt des distances de plus en plus petites. On dira de son mouvement qu’il est décéléré, puisque la norme de la vitesse diminue au cours du temps.
Vérifions également que, dans ce deuxième cas, le vecteur accélération \(\overrightarrow{a}\) est bien cohérent avec les vecteurs vitesse \(\overrightarrow{v}\) (Fig.4.):

Etant donné que le mouvement est rectiligne, les 3 vecteurs ont la même direction (horizontale), on peut donc utiliser la relation \((4)\):
\begin{equation}
\Delta{v_{2}} = {v_{3}} – {v_{1}} \Leftrightarrow \Delta{v_{2}} = 1 – 3 = – 2 \big[\frac{m}{s}\big]
\end{equation}
C’est ensuite le même raisonnement pour parvenir au vecteur accélération: puisque l’intervalle de temps considéré est de 2 secondes (\(\Delta t= t_{3}-t_{1} \, = \, 2[s]\)), d’après la relation \((2)\), on aura un vecteur accélération de \(-1 \, m/s²\).
Je retiens…
Si le vecteur accélération (négatif) est parallèle mais de sens opposé au vecteur vitesse (positif), la valeur de la vitesse diminue régulièrement au cours du temps.
MRUA avec vitesse négative et accélération positive
C’est le troisième cas de figure, le vecteur vitesse \(\overrightarrow{v}\) est dans le sens opposé au référentiel mais le vecteur accélération \(\overrightarrow{a}\) est orienté dans le sens du référentiel. La composante scalaire de la vitesse \(v\) est donc négative tandis que celle de l’accélération, \(a\), est positive.
Le diagramme d’un tel mouvement ressemble à ceci:
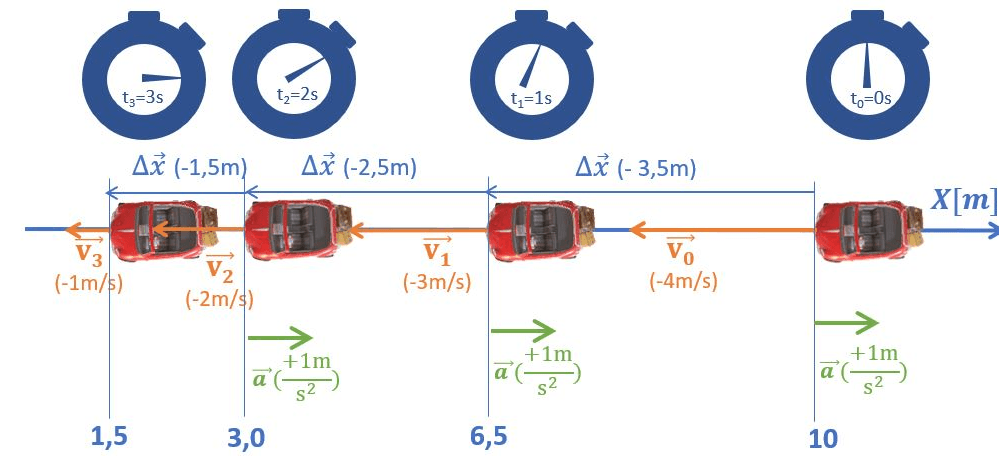
Dans ce cas, on introduira la valeur \(a=+1m/s²\) dans l’expression \((2)\) . On en déduira donc que, pour chaque seconde de mouvement, la composante scalaire du vecteur vitesse augmente de \(1m/s\), ce qui est conforme à la Fig.5.
Attention
La valeur de \(-3m/s\) est bien de \(1m/s\) supérieure à la valeur de \(-4m/s\). On parle dans ce cas des composantes scalaires des vecteurs qui augmentent au cours du temps puisque \(a\) est positive. Par contre, la norme des vecteurs (qui elle, est toujours positive), diminue au cours du temps. En effet, la voiture avance de moins en moins vite: \(\lVert -3 \lVert < \lVert -4 \lVert \). Et donc, quand on parle de la norme, on s’intéresse uniquement à la valeur du vecteur tandis que, quand on parle de composante scalaire, le signe contient une information supplémentaire: le sens du vecteur!
La voiture avance donc de moins en moins vite et parcourt des distances de plus en plus petites. On dira de son mouvement qu’il est décéléré, puisque la norme de la vitesse diminue au cours du temps.
Vous pourrez vérifier que, dans ce troisième cas, le vecteur accélération \(\overrightarrow{a}\) est bien orienté vers la droite, en construisant une figure similaire aux Fig.2 et 4.
Dans ce cas, nous avons:
\begin{equation}
\Delta{v_{2}} = {v_{3}} – {v_{1}} \Leftrightarrow \Delta{v_{2}} = -1 – (-3) = + 2 \big[\frac{m}{s}\big]
\end{equation}
Cette variation de vitesse \(\Delta{v_{2}}\) ayant lieu en un temps \(\Delta t= t_{3}-t_{1} \, = \, 2[s]\), le vecteur accélération aura une valeur de \(+1 \, m/s²\), d’après la définition \((2)\).
Je retiens…
Si le vecteur accélération (positif) est parallèle mais de sens opposé au vecteur vitesse (négatif), la norme de la vitesse diminue régulièrement au cours du temps.
MRUA avec vitesse négative et accélération négative
C’est le dernier cas de figure, le vecteur vitesse \(\overrightarrow{v}\) est dans le sens opposé au référentiel tout comme le vecteur accélération \(\overrightarrow{a}\). Leurs composantes scalaires sont donc négatives.
Le diagramme d’un tel mouvement ressemble à ceci:

Dans ce dernier cas de figure, et d’après le même raisonnement que précédemment, on introduira la valeur \(a=-1m/s²\) dans l’expression \((2)\) . On en déduira donc que, pour chaque seconde de mouvement, la composante scalaire du vecteur vitesse diminue de \(1m/s\), ce qui est conforme à la Fig.6.
Attention
La valeur de \(-2m/s\) est bien de \(1m/s\) inférieure à la valeur de \(-1m/s\). On parle dans ce cas des composantes scalaires des vecteurs qui diminuent au cours du temps puisque \(a\) est négative. Par contre, la norme des vecteurs (qui elle, est toujours positive), augmente au cours du temps. En effet, la voiture avance de plus en plus vite puisque \(\lVert -2 \lVert > \lVert -1 \lVert \). Même combat qu’au point précédent!
La voiture avance donc de plus en plus vite et parcourt des distances de plus en plus grandes. On dira de son mouvement qu’il est accéléré, bien que l’accélération soit négative, puisque la norme de la vitesse augmente au cours du temps.
Vous pourrez vérifier que, dans ce dernier cas, le vecteur accélération \(\overrightarrow{a}\) est bien orienté vers la gauche, en construisant une figure similaire aux Fig.2 et 4.
Dans ce cas, nous avons:
\begin{equation}
\Delta{v_{2}} = {v_{3}} – {v_{1}} \Leftrightarrow \Delta{v_{2}} = -4 – (-2) = – 2 \big[\frac{m}{s}\big]
\end{equation}
Les vecteurs \(\Delta{\overrightarrow{v}_{2}}\) et \(\overrightarrow{a}\) ont tous deux des composantes scalaires négatives, ils sont donc bien orientés vers la gauche. On vérifiera que le vecteur accélération a bien une valeur de \(-1 \, m/s²\).
Je retiens…
Si le vecteur accélération (négatif) est parallèle et de même sens que le vecteur vitesse (négatif), la norme de la vitesse augmente régulièrement au cours du temps.
Conclusion
Ce qui définit l’accélération ou la décélération (au sens commun du terme), ce n’est pas uniquement le signe de l’accélération mais son signe par rapport à celui de la vitesse!
- Si a et v sont de même signe \(\Leftrightarrow \) \(\overrightarrow{a}\) et \(\overrightarrow{v}\) sont de même sens \(\Leftrightarrow \) il y a bien accélération au sens commun du terme: la norme du vecteur vitesse augmente régulièrement et on va de plus en plus vite!
- Si a et v sont de signes opposés \(\Leftrightarrow \) \(\overrightarrow{a}\) et \(\overrightarrow{v}\) sont de sens opposés \(\Leftrightarrow \) il y a alors décélération au sens commun du terme: la norme du vecteur vitesse diminue régulièrement et on va de moins en moins vite!

On retiendra donc que le signe (de la composante scalaire) d’un vecteur me donne sons sens! Etant donné que le vecteur vitesse doit être imaginé comme un vecteur enfoncé dans le capot-avant de la voiture, le signe de \(v\) me donnera le sens du mouvement (dans le sens du référentiel ou dans le sens opposé); tandis que le signe de \(a\) étudié par rapport au signe de v me donnera une indication sur l’accélération au sens commun du terme.
Je n’oublie surtout pas que pour avoir une accélération (pour aller de plus en plus vite), il faut que le vecteur \(\overrightarrow{a}\) « pousse » dans le même sens que le vecteur \(\overrightarrow{v}\). Si \(\overrightarrow{a}\) s’oppose à \(\overrightarrow{v}\), alors on freine! Il s’agit de la décélération au sens commun du terme!
N.B. Si cet article t’a aidé(e) dans ton travail, merci de me laisser un like ou un commentaire positif afin que j’aie un retour sur mon travail. C’est en effet frustrant de travailler sans connaitre le bénéfice de son travail 😉 … Merci et bon courage à toi!!!
Retrouve ce cours en vidéo sur MRUA – approche vectorielle
\(\\\)
Il y a aussi un article qui reprend 4 exercices sur le MRUA, résolus pas à pas! C’est par ici!






Merci bcp, cet article m’a vraiment aidé tout comme celui sur le MRU. J’ai en général de la peine à comprendre la physique et le math et c’est frustrant car je sais aussi que j’ai le niveau. Mais ces 2 cours sont bien rentrés.
Merci pour ton retour Louis! Bon courage pour la suite!