Recevez gratuitement
mon livret!

Tu te rappelles de l’aire d’un triangle?
\(Aire=\frac{Base\ \bullet \ Hauteur}{2}\)
Alors, tu sais le plus difficile pour calculer le déplacement!
La raison est simple! Si tu traces le graphique de la vitesse en fonction du temps (simplement l’allure, pas besoin d’être hyper précis!), l’intégrale de cette fonction (ou pour faire plus simple, l’aire sous la courbe), représente le déplacement \(\Delta x\)
Pas de long discours d’explication du comment du pourquoi ici, ça, c’est fait dans la vidéo dont je parle en fin d’article! Là, je vais juste te montrer l’application de ce truc dans 4 exercices repris dans des questions de l’EXMD (Examen d’entrée en Médecine/Dentisterie, en Belgique)! Allons-y, il n’y en a pas pour longtemps!
A l’atterrissage, un avion touche le sol à une vitesse de 180 km/h. Après une décélération uniforme, il s’immobilise 10s plus tard.
Quelle distance au sol parcourt-il avant de s’arrêter?
A. 100m
B. 250m
C. 500m
D. 1000m
Première étape, tu transformes tes unités et tu te fais un mini schéma de la situation, le cerveau est plus efficace sur des images que sur du texte! ça donne, ça:
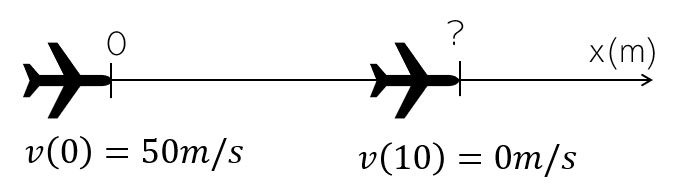
On te parle d’une décélération et d’une distance \(\Rightarrow\) TU DESSINES L’ALLURE DU GRAPHE \(v(t)\) et ça donne ça:
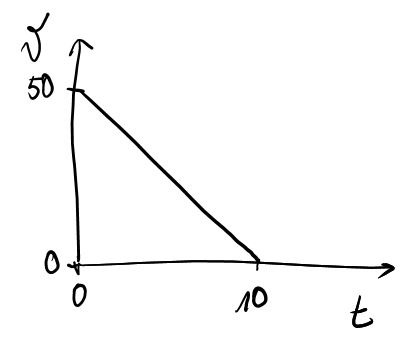
Et tu exprimes que l’aire représente le déplacement! et ça donne ça (puisque tu sais que l’aire d’un triangle, c’est \(\frac{B.H}{2}\)):
\(\\ \)
\(\Delta x = \frac{10.50}{2}=250m\)
\(\\ \)
FINITO! Réponse B
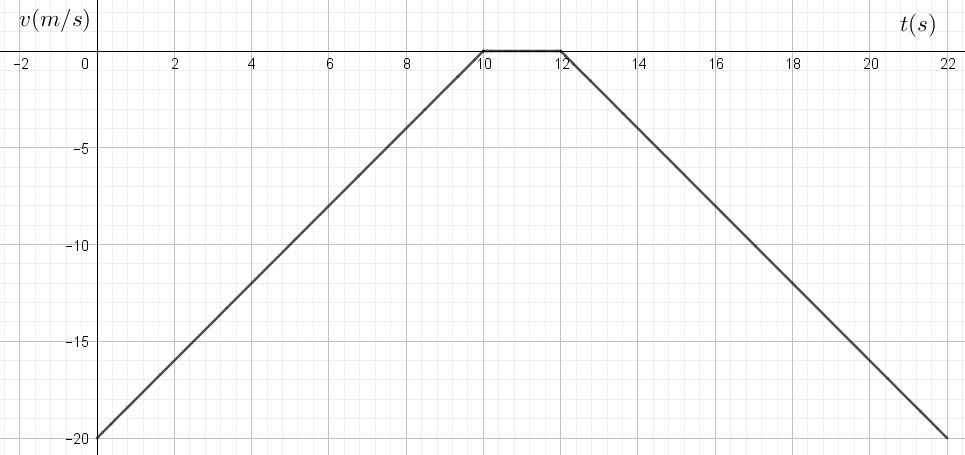
On considère le mouvement rectiligne d’un mobile. Le graphique ci-dessous représente la vitesse du mobile en fonction du temps sur une durée de 12 secondes.
Quelle est la distance parcourue par le mobile pendant ces 12 secondes?
A. 48m
B. 64m
C. 80m
D. 92m
Alors, là, c’est clair! Le graphique est déjà fait pour toi! Plus qu’à colorier les formes les plus simples et à répondre à la question posée!\(\\ \)
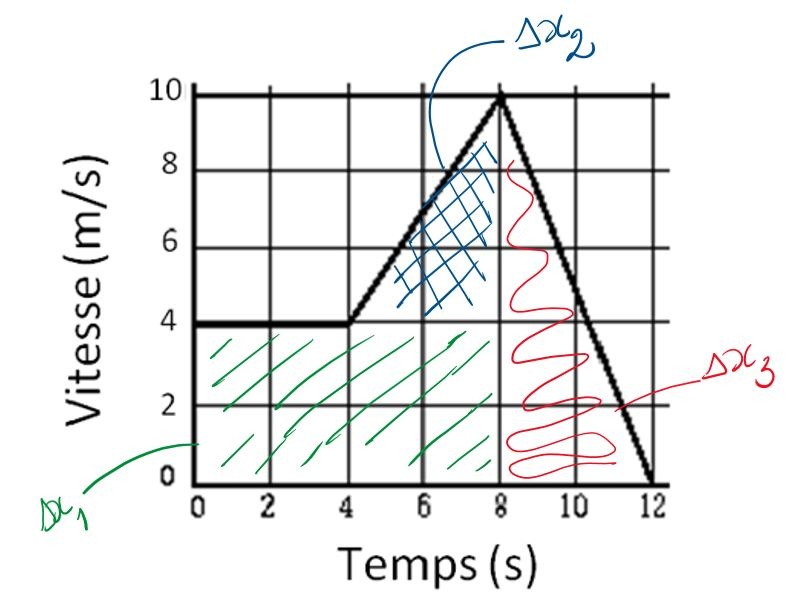
Alors, c’est clair qu’il n’y a pas qu’une réponse possible! On choisit ce qu’on veut comme zones! Pour mon choix, ça donne ça:
\(\Delta x_{1}=4.8=32m\)
\(\\ \)
\(\Delta x_{2}=\frac{4.6}{2}=12m\)
\(\\ \)
\(\Delta x_{3}=\frac{4.10}{2}=20m\)
\(\\ \)
Et donc:
\(\\\)
\(\Delta x=32+12+20=64m\)
\(\\ \)
FINITO! Réponse B
Une voiture subissant une accélération uniforme passe de 0 à 72 km/h sur une distance de 100m.
En combien de temps a-t-elle atteint cette vitesse?
A. 5s
B. 10s
C. 15s
D. 20s
Alors, là, tu vois qu’on est plus proche du 1er exercice, mais il y a quand même un truc qui cloche, on ne sait pas compléter le graphique avec des valeurs chiffrées, il nous manque le temps!
Ben oui, c’est logique, puisque c’est la question posée!
Dans ce cas, NO STRESS! Comme à chaque fois en physique, quand tu ne sais pas, tu inventes! Non, je plaisante! Quand tu ne sais pas, tu laisses le symbole de la grandeur, ici: \(\Delta t\)!
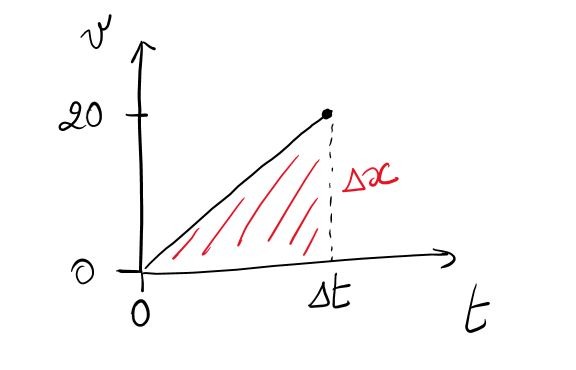
\(\\ \)
On calcule l’aire rouge:
\(\Delta x=\frac{\Delta t.20}{2}=10.\Delta t\)
\(\\ \)
Or, on sait que le déplacement vaut 100m et donc que \(\Delta x=100m\)
\(\\ \)
Et donc:
\(100=10.\Delta t\)
\(\Leftrightarrow \Delta t = 10s\)
\(\\ \)
Réponse B
Retrouve ces exercices en vidéo (avec quelques explications en plus): Clique ici!
Si tu veux avoir accès à tous les exercices, de tous les genres, sur le MRUA, alors, C’est par ici et par ici!
Bonne continuation dans ton apprentissage de la physique!
Hello,
Aujourd’hui, je te propose une série de 4 exercices sur la force électrique (ou électrostatique, c’est encore mieux). Ils sont progressifs, et si tu t’efforces de comprendre chacune des étapes, tu verras que ce n’est pas si compliqué!
Avant de commencer, assure-toi que tu maitrises ce que je raconte ici! C’est un petit rappel de la théorie de la force électrique (loi de Coulomb)!
C’est le cas le plus simple, on l’a déjà rencontré dans l’article traitant de la théorie.
La force électrique entre deux charges identiques est de 10N. Que devient cette force lorsque:
- La distance qui sépare les charges double?
- Une des deux charges double?
- Chacune des deux charges double?
- La distance qui sépare les charges est réduite d’un facteur 3?
On nous parle donc clairement de deux charges électriques situées à une certaine distance l’une de l’autre. On peut donc, sans problème s’en référer à la loi de Coulomb. Par ailleurs, on ne nous parle pas de la direction des forces, mais uniquement de leur valeur (scalaire), on n’a donc pas besoin de s’embêter avec l’orientation des forces. On a:
1. La distance intervient au carré (\(R^{2}\)): si la distance double, on se retrouve avec un facteur \((2R)^{2}=4R^{2}\) au dénominateur. La force est divisée par un facteur 4 et vaut 2,5N
\(\\\)
2. Le produit \(\lvert q_{1}.q_{2}\rvert\) devient \(\lvert 2q_{1}.q_{2}\rvert\). La force est simplement doublée et vaut 20N.
\(\\\)
3. Le produit \(\lvert q_{1}.q_{2}\rvert\) devient \(\lvert 2q_{1}.2q_{2}\rvert\). La force est quadruplée, elle vaut 40N.
\(\\\)
4. On se retrouve avec un facteur \((\frac{R}{3})^{2}=\frac{R^{2}}{9}\) au dénominateur. On a:
\(\\\)
Dans cet exercice, il y a 3 charges électriques et on détermine la force résultante exercée par deux d’entre elles sur la 3ème.
Sur la figure ci-dessous, on suppose que les deux charges électriques ponctuelles Q situées aux points se trouvant sur l’axe y sont positives. Si on place une charge ponctuelle négative -Q au point P, comment sera orientée la force électrique résultante agissant sur cette dernière?
- Vers la gauche, le long de l’axe x
- Vers la droite, le long de l’axe x
- Verticalement vers le bas
- Verticalement vers le haut
Ici, le mot « résultante » est important. Il nous rappelle (au cas où on l’aurait oublié) qu’il y a, à proximité de la charge \(-Q\), deux autres charges: il y a donc deux vecteurs force à prendre en compte. D’après les solutions proposées, on remarque qu’il n’est pas nécessaire de faire des calculs numériques; d’ailleurs, on ne nous donne aucune valeur. Pourtant, puisqu’on doit additionner des vecteurs, leurs intensités ont de l’importance, mais il suffit de les comparer les unes aux autres.
On remarque qu’entre chacune des deux charges \(Q\) (situées sur l’axe y) et la charge \(-Q\), il y a la même distance. Comme, par ailleurs, les charges sont identiques, la force d’attraction entre la charge \(Q\) située en-haut et la charge \(-Q\), a la même valeur que la force d’attraction entre la charge \(Q\) située en bas et la charge \(-Q\).
Attention: soucre d’erreur: ne pas dessiner les forces au bon endroit. On nous parle de la force résultante SUR LA CHARGE \(-Q\); c’est donc sur elle et uniquement sur elle, qu’il faut dessiner les forces électriques.
Comme les charges s’attirent (elles sont de signes opposés), les deux vecteurs que nous devons dessiner partent de la charge \(-Q\) et vont vers chacune des charges \(Q\).
\(\\\)
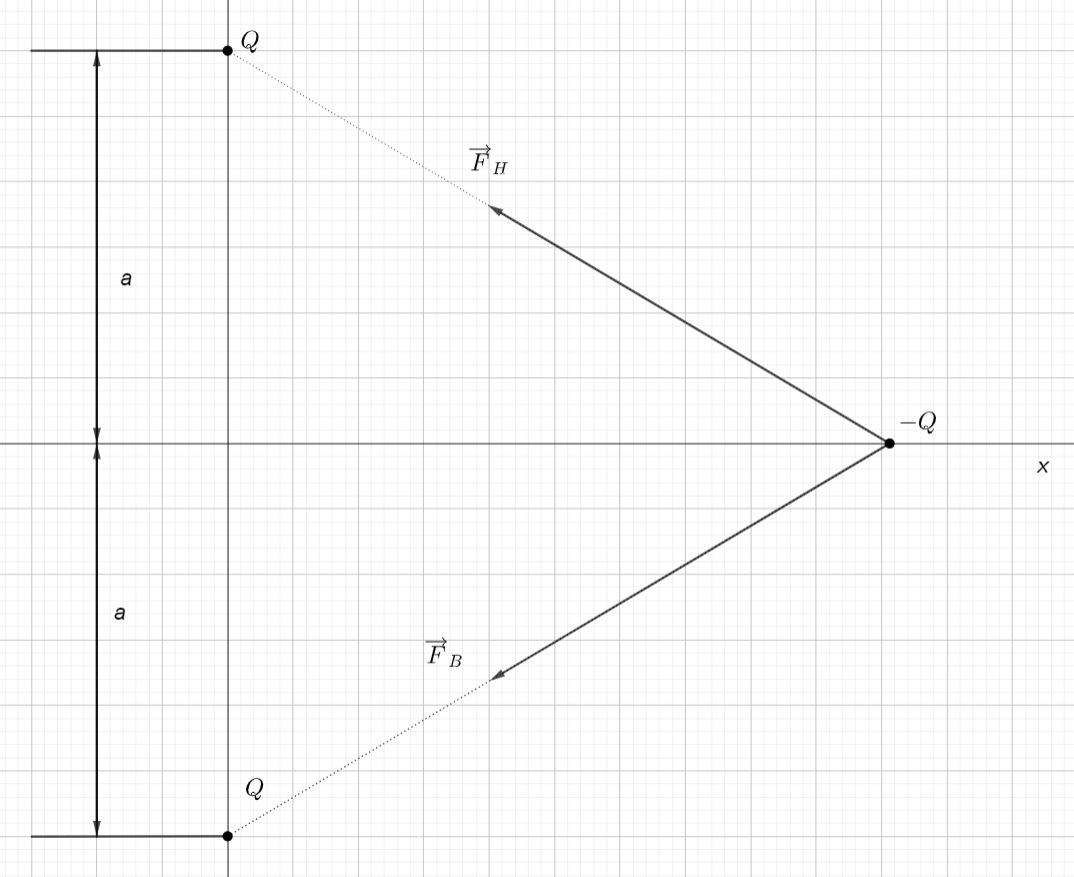
\(\\\)
Pour additionner les forces (puisqu’elles n’agissent pas dans les mêmes directions), il faut les décomposer:
\(\\\)
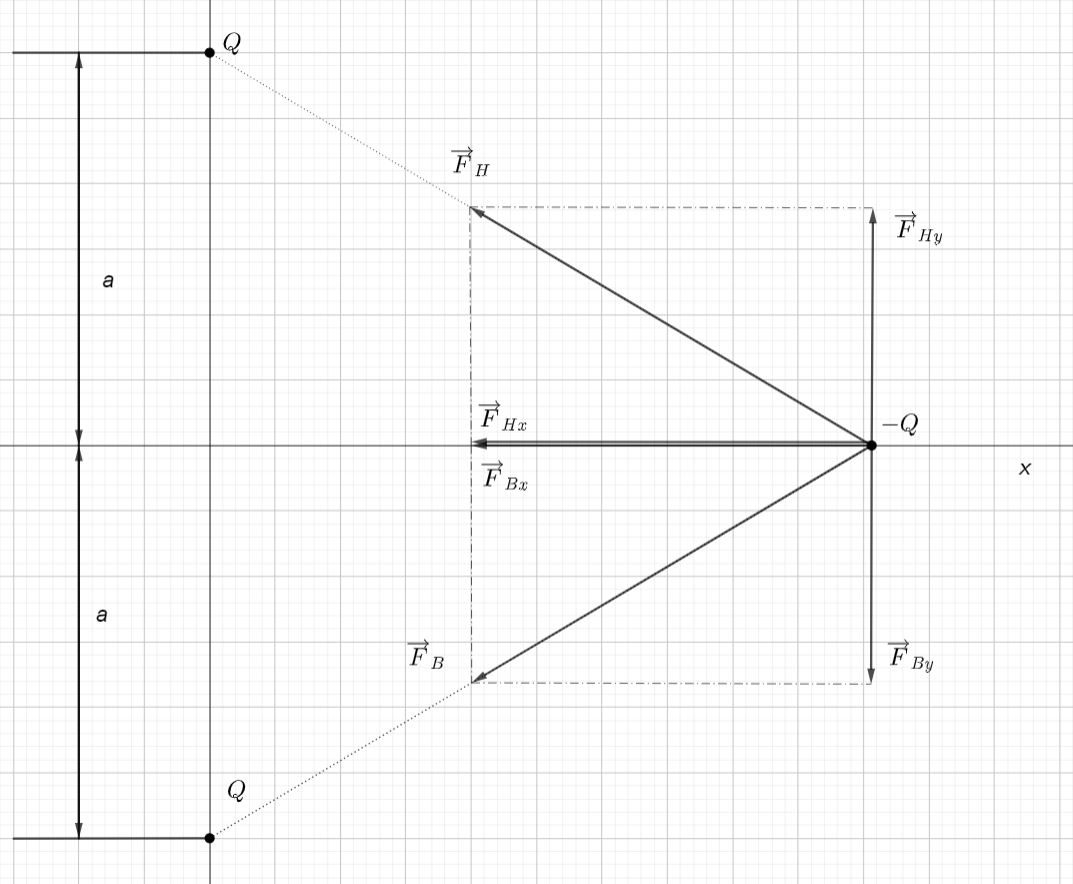
\(\\\)
Les composantes verticales \(\vec{F}_{Hy}\) et \(\vec{F}_{By}\) ont bien entendu la même valeur et sont de sens opposé, elles s’annulent.
Il reste les deux composantes horizontales, \(\vec{F}_{Hx}\) et \(\vec{F}_{Bx}\), identiques et dans le mêmes sens qui vont donner lieu à une force horizontale deux fois plus grande vers la gauche. La bonne réponse est donc « 1.Vers la gauche, le long de l’axe x ».
Remarquons que tout le raisonnement est nécessaire puisque, si une des deux forces était plus grande que l’autre, la force résultante ne serait pas horizontale mais oblique.
Si tu as bien pigé l’exercice II, celui-ci ne devrait te poser aucun problème!
Trois charges électriques identiques sont disposées sur les coins d’un carré comme le représente le dessin suivant. On place une charge électrique positive dans le quatrième coin.
\(\\\)
\(\\\)
Quelle est la direction de la force résultante qui s’exerce sur cette charge?A. Vers la droite.
B. Vers le bas.
C. Vers l’intérieur du carré.
D. Suivant la diagonale du carré.
C’est similaire à l’exercice précédent, à ceci près qu’on ne donne pas le signe des 3 charges déjà présentes. A toi de voir si cela change quelque chose ou pas…
\(\\\)
\(\\\)
…
\(\\\)
\(\\\)
…
\(\\\)
On corrige ensemble?
Si on envisage les deux cas de figure: soit les 3 charges sont positives et les forces électriques avec \(+Q\) sont répulsives, c’est le schéma de gauche. Soit les 3 charges sont négatives et les forces sont alors attractives, c’est le schéma de droite. On se souvient qu’on étudie la charge déposée sur le sommet inférieur droit; on ne dessine les forces que sur cette charge.
\(\\\)
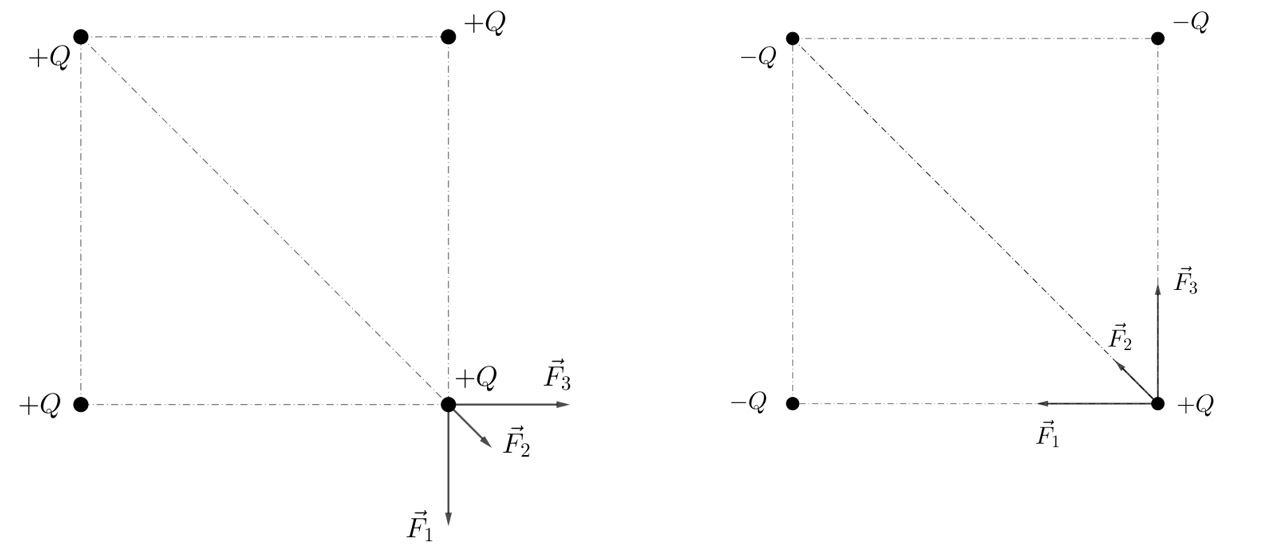
\(\\\)
La distance entre la charge \(+Q\) d’intérêt et la charge parfaitement au-dessus d’elle est la même que la distance entre la charge d’intérêt et celle parfaitement à sa gauche, puisque les charges sont sur les sommets d’un carré. Les forces numérotées \(\vec{F}_{1}\) et \(\vec{F}_{3}\) ont donc la même intensité. Par contre, la charge située au bout de la diagonale est à une distance \(\sqrt{2}\) fois plus grande (en effet, si le côté du carré est noté \(a\), la diagonale vaut \(\sqrt{2}a\)) et la force \(\vec{F}_{2}\) sera donc 2 fois plus petite que les deux autres (rappelle-toi que la distance intervient au carré! Si tu as oublié, vas relire l’exercice I).
Il faut additionner les vecteurs \(\vec{F}_{1}\), \(\vec{F}_{2}\) et \(\vec{F}_{3}\). Il est évident que la somme de \(\vec{F}_{1}\) et \(\vec{F}_{3}\) est orientée le long de la diagonale. Le vecteur \(\vec{F}_{3}\) s’ajoutera ensuite simplement à \(\vec{F}_{1}+\vec{F}_{2}\). La réponse est donc la D! Dans le 1er cas, la résultante sera le long de la diagonale et sortante, dans le second, elle sera le long de la diagonale et rentrante!
La dernière difficulté consiste à combiner les 3 exercices qui précèdent, en ce sens qu’il faut trouver l’orientation d’une force résultante et sa valeur.
Trois charges électriques ponctuelles sont disposées comme sur le schéma ci-dessous:
\(\\\)
Que doit valoir la charge \(Q\) pour que la force résultante s’exerçant sur la charge de \(-2nC\) soit nulle? (le symbole nC signifie nanoCoulomb)A. -1/3 nC
B. -1 nC
C. -2 nC
D. -3 nC
\(\\\)
Je ne sais pas si tu as remarqué, mais on combine ici tout l’article: le fameux nano qui te dit \(10^{-9}\), la valeur des charges et leurs distances respectives qui vont te permettre d’utiliser la loi de Coulomb pour calculer les intensités des forces électriques, et enfin, le fameux terme « résultante » qui te rappelle que tu te prépares à additionner plusieurs forces!
S’ajoute une nouveauté: il faut que la résultante SUR LA CHARGE DE -2nC soit nulle. On se concentre donc, exclusivement sur la charge centrale pour dessiner les vecteurs force! Tu sais que cette charge est soumise à deux vecteurs force (la force qui vient de la 1ère charge et celle de la 3ème). Si tu veux une résultante nulle, il te faut une force vers la gauche et une force vers la droite!
\(\\\)
C’est bon, j’ai assez bossé, là, c’est à ton tour…
\(\\\)
…
\(\\\)
Alors, bon, c’est pas mal d’avoir vu tout ce qui précède, mais avant de te lancer tête baissée dans l’application de la loi de Coulomb, observe que les distances respectives de \(5cm\) et de \(15cm\); ben, Y’a un facteur 3 qui les sépare! Du coup, pas besoin de se casser la tête! On veut deux choses:
Si tu te souviens du premier énoncé, si la distance est divisée par \(3\), la force est divisée par \(9\)! Donc pour obtenir deux forces de même intensité, il faudrait que la charge \(q_{1}\) soit 9 fois plus petite que la charge \(q_{3}\) puisqu’elle est 3 fois plus proche de la charge \(q_{2}\) (et que la distance intervient au carré; t’as pas oublié!)! On a donc:
Il ne reste plus qu’à trouver le signe de la charge (même si, franchement, ils nous aident, là, sur ce coup-là, avec leurs propositions… mais bon, ça permet de se rassurer):
Puisque les charges \(q_{2}\) et \(q_{3}\) se repoussent, \(q_{3}\) exerce sur \(q_{2}\), une force vers la gauche. Il faut donc que \(q_{1}\) exerce sur \(q_{2}\) une force vers la droite. En d’autres termes, il faut que \(q_{1}\) pousse \(q_{2}\) plus loin. On veut une répulsion, il faut le même signe que \(q_{2}\) et \(q_{1}\) est bien négative! TADAMMMM!!!
C’est bien la réponse A.
\(\\\)
Rmq: Si tu ne penses pas à réfléchir ainsi et que tu appliques la loi de Coulomb pour trouver la valeur de la première force, tu vas trouver ceci:
Rappelle-toi que tu n’as pas de calculatrice et que c’est pas super sympa ce calcul…. signe qu’il y a plus simple! Ceci dit, tu peux toujours t’en sortir en remarquant que \(0,15=\frac{3}{20}\). Tu aurais:
Mais, c’est quand même vachement plus compliqué, parce qu’après, tu dois exprimer que la force entre \(q_{1}\) et \(q_{2}\) doit avoir la même valeur. Tu as:
\(\\\)
OUFTI!!!! Je te conseille quand même de scruter les énoncés et de voir si les distances considérées sont multiples l’une de l’autre!!!
\(\\\)
\(\\\)
Ceci clôture cet article. En ce qui concerne l’examen d’entrée en Médecine/dentisterie (je propose des ressources YT ici), il n’y a pas eu plus compliqué ces deux dernières années. Par contre, si tu veux vraiment te préparer à vivre un bac scientifique, c’est bien de relever encore un tantinet le niveau. Si tu es motivé(e), je te propose au bas de cette page, un cahier d’exercices progressifs avec solutions pour la modique somme de 27€! Et comme tu peux toujours me poser tes questions, je parie que tu ne trouveras pas moins cher ailleurs!
\(\\\)
Si tu en as ta dose, très bien, mais si je t’ai aidée, donne moi un like ici tout en bas de la page! Ben quoi, tout travail mérite salaire, non?
\(\\\)
Allez, bonne chance et bon courage pour la suite! Si tu préfères les supports vidéos, la théorie et la comparaison entre la force électrique et la force gravifique (le poids, quoi!) sont repris ici!
\(\\\)
Le cahier est structuré de la façon suivante:
- Rappel des formules et valeurs importantes
- Six exercices-type résolus en détail, suivis d’un ou plusieurs exercices pour s’entraîner
- Les solutions détaillées des exercices supplémentaires

Pour te procurer ce cahier, clique sur le bouton « Acheter » de Paypal ci-dessous!
Bonjour à toutes et à tous,
Aujourd’hui, tu vas comprendre la force électrostatique via la loi de Coulomb. Comment? Et bien, d’abord, en se rappelant qu’on parle, comme pour toutes les forces, d’une bestiole vectorielle. Et donc, tu n’oublieras pas la technique de décomposition d’un vecteur, comme ici avec la force gravifique. Force gravifique, électrique ou vitesse, ce sont tous des vecteurs qu’on peut (qu’on doit souvent) décomposer. Et ensuite, en parvenant à faire parler en français la loi de Coulomb pour qu’elle te révèle vraiment ce qu’elle contient comme information!
La charge électrique se mesure en Coulomb (comme une masse se mesure en kilogramme), elle est portée par le très célèbre électron et par son, non moins connu acolyte, le proton!
Il te faut absolument (si si, j’insiste) connaitre la valeur de la charge élémentaire: \(1,602.10^{-19} C\)
Ce qui différencie le proton de l’électron, c’est le signe de la charge! Mais ça, tu le sais quand même…
Tu vois que le \(Coulomb \) est une unité vachement, vachement grande! \(1,602.10^{-19} C\), c’est (je ne l’écrirai qu’une fois): \(0,0000000000000000001602 C\)
\(\\\)
Il faut donc se lever tôt pour rassembler une charge de \(1C\) et en électrostatique, on parlera souvent de plus petites bestioles, que tu dois connaitre aussi, je suis vraiment désolée… Je te les présente, en commençant par une des plus petites:
- Le femtocoulomb: \(1\ fC = 1.10^{-15}C\). C’est quand même vachement petit, on en parlera peu.
- Le picocoulomb: \(1\ pC = 1.10^{-12}C\). C’est déjà mieux, tu risques de le rencontrer un jour ou l’autre.
- Le très célèbre nanocoulomb: \(1\ nC = 1.10^{-9}C\). Bon, nano, tu entends 9, ça va, c’est pas trop compliqué à retenir!
- Le plus célèbre encore microcoulomb: \(1\ µC = 1.10^{-6}C\). Ne l’oublie pas, celui-là!
- Le quasi pas utilisé millicoulomb: \(1\ mC = 1.10^{-3}C\). C’est déjà trop gros, on s’arrête là!
Du coup, si tu mets dans un bol, \(3*100g\) de riz, tu as une masse résultante de \(300g\) de riz, c’est clair! Et bien, si tu rassembles 1 milliard (\(1.10^{9}\)) d’électrons, tu as une charge résultante (ou nette ou totale) de:
\(1.10^{9}*1,602.10^{-19}=1,602.10^{-10}C\)
On dira: la charge nette vaut \(q=1,602.10^{-10}C\)! Ah oui, je ne t’avais pas encore dit; si en physique, on attribue la lettre m pour la masse, on attribue la lettre q pour la charge!
\(\\\)
Bon, ok, et comment fait-on pour rassembler 1 milliard d’électrons? …. on frotte! Les physiciens parlent de tribologie. Du coup, quand le frottement engendre des transferts de charges (c’est l’objet du point suivant), on parle de triboélectrostatique! Tout un programme!
Pour comprendre les forces qui existent entre les atomes, il faut d’abord se souvenir de ce qu’est un atome, c’est évident. Je te propose deux objets: ta bouteille d’eau (super important d’hydrater ton cerveau quand tu bosses) et ton chat (si tu en as un, il est certainement occupé à se prélasser au soleil et à te montrer qu’il n’y a rien de mieux qu’une vie de chat… tant pis pour nous, ce sera pour une autre fois)!
Ces deux objets sont, par nature, électriquement neutres. Ils contiennent en effet autant de protons que d’électrons!
Que se passe-t-il si on frotte l’un contre l’autre? Pour répondre à cette question, il faut regarder la série triboélectrique: on voit que la fourrure de chat occupe une place supérieure à celle du PVC, qui est loin en bas, du côté des matières négatives.
\(\\\)

En frottant l’un contre l’autre, la fourrure deviendra positive et le PVC négatif. Autrement dit, c’est le chat qui cèdera, par frottement, des électrons (pas tous, hein) à la bouteille de PVC.
Et donc, le chat, ayant perdu des électrons, possède maintenant plus de protons que d’électrons: il développe une charge nette POSITIVE.
La bouteille de PVC gagne des électrons supplémentaires, elle a plus d’électrons que de protons: elle développe la même valeur de charge que le chat, mais NEGATIVE.
\(\\\)
Et donc, si on frottait une baguette de verre sur le chat, ça changerait quoi???
\(\\\)

C’est maintenant le verre qui est plus haut placé, c’est donc lui qui deviendra positif en cédant ses électrons au chat; qui devient négatif! Attention, j’espère que tu n’as pas parlé de transfert de protons! Les protons sont coincés dans le noyau, ils ne peuvent pas en sortir par simple frottement!!! Les protons ne se déplacent pas dans la matière!
\(\\\)
Bon, maintenant que l’on sait ce qu’est la charge et comment la créer, on va pouvoir s’amuser avec les charges!
Alors, ça, pour le coup, tout le monde le sait: les opposés s’attirent! On vérifie donc par l’expérience que deux baguettes de verres, frottées contre un chat se repoussent! Deux charges positives se repoussent, en effet!
Que deux bouteilles de PVC, frottées contre un chat …. ben, se repoussent aussi, puisque deux charges négatives se repoussent!
Par contre, la baguette de verre est attirée par la bouteille de PVC et vice-versa! Enfin, pour autant qu’elles aient été toutes les deux frottées contre un chat!
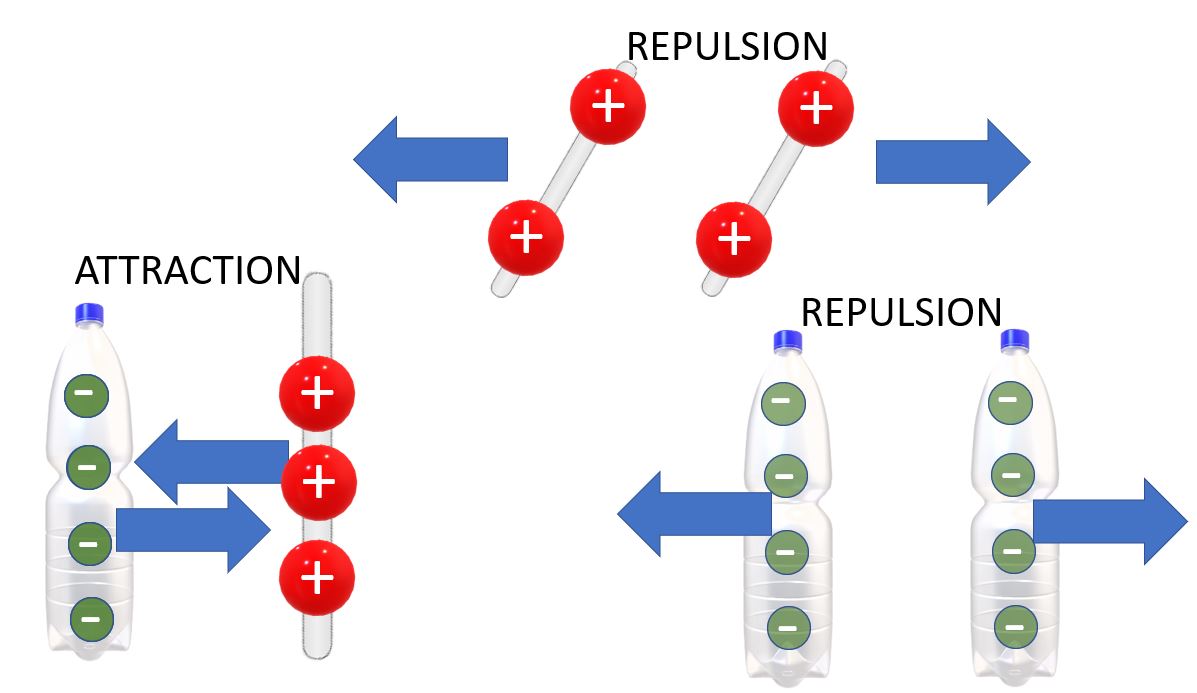
Il nous reste à évaluer ces forces en Newton! C’est Coulomb qui s’y est collé en 1785 et qui nous a sorti une belle petite formule que voici! Je te fais grâce de l’explication de sa technique expérimentale, mais si elle t’intéresse, j’en parle ici!
\(\\\)

\(\\\)
Evidemment, avant de faire parler cette formule en français, il faut comprendre ses paramètres. On y rencontre:
Bon, une dernière chose avant de faire parler cette formule! Remarque bien qu’elle est purement scalaire, ce qui veut dire que tu ne vois apparaitre de petite flèche nulle part! Pourtant, la force, c’est un vecteur! Cela signifie donc que Coulomb ne te renseigne QUE sur la valeur des forces, pas sur leur direction (chacun son job, hein!)! Pour la direction, tu traces une ligne imaginaire entre les deux charges, tu regardes leurs signes, puis tu traces les vecteurs Force: Répulsion ou Attraction?
\(\\\)

\(\\\)
J’ai pour habitude de dire que, si, à chaque fois que tu vois une formule en physique, tu prends le temps de la « lire » en français, alors, tu sauras toujours quand tu dois l’appliquer! Si on veut se la péter, on dira: « Je connais parfaitement le champ d’application de cette formule »! En bref, je sais faire mes exercices, quoi!
\(\\\)
DONC! QUE DIT COULOMB?
Il dit que (lis ce qui suit en regardant la formule de Coulomb, juste en-dessous):
Tu sais que ces deux charges s’attirent (ou se repoussent) avec une force d’origine électrostatique, dont l’intensité est donnée par:
\(\\\)
\(\huge F=\frac{1}{4\pi\epsilon_{0}}\frac{\lvert q_{1}.q_{2}\rvert}{R^{2}}\)
Quelle force existe entre un proton et un électron d’un atome d’hydrogène, si on suppose (vaste blague, mais bon…) que l’électron subit une orbite circulaire (selon le modèle de Bohr) de rayon égal à \(0,53.10^{-10}m\)?
Que nous dit Coulomb, encore?
Un électron et un proton ont des charges opposées, il s’agit donc de forces d’attraction.
L’intensité de chacune de ces forces est donnée par (Youhou! J’applique enfin Coulomb!):
\(\\\)
\(\large F=9.10^{9}\frac{\lvert (-1,602.10^{-19}).(+1,602.10^{-19})\rvert}{(0,53.10^{-10})^{2}}=8,2.10^{-8}N\)
Bon, ça peut paraitre petit comme force, mais n’oublie pas qu’on joue avec un électron et un proton dont les masses sont de \(9,11.10^{-31}kg\) et \(1,67.10^{-27}kg\) respectivement!
L’accélération qui en résulte est donc bien réelle!
\(\\\)
Tu es prêt à te mettre au travail! Prochain article, ce sera une série de quelques exercices progressifs qui concernent notre ami Coulomb! Bref, de quoi vraiment travailler!
\(\\\)
MRUA – Etude des graphiques et équations associées
Pourquoi la vitesse et l’accélération peuvent-elles être positives ou négatives?
Exercices résolus en vidéo
Je pars du principe que tu sais utiliser l’outil graphique, parce que, tu es allé lire l’exercice résolu n°1 qui se trouve ici!
Si ce n’est pas le cas, dépêche-toi, il ne faut pas plus de 10 min!C’est bon? Qu’as-tu retenu? Normalement, que la pente de la tangente au graphique v(t) représente l’accélération instantanée puisque:
\begin{equation}
\ \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta {v}}{\Delta t_{ }}=a
\end{equation}
Mais aussi que l’aire comprise entre la courbe v(t) et l’axe du temps représente la valeur du déplacement \(\Delta x \) puisque:
\begin{equation}
\ v*\Delta t = \Delta x
\end{equation}
Exercices corrigés pas à pas disponibles ici! Fascicule reprenant:
- 3 pages de synthèse sur TOUT ce qu’il faut ABSOLUMENT comprendre avant de se lancer tête baissée dans les exercices sur le MRUA (et de perdre son temps) !
- Les 29 exercices ci-dessous corrigés dans les moindres détails en 41 pages!
Bref, l’équivalent de plus de 10 heures de cours pour moins de 30€ !!!
Clique sur le bouton « Acheter » ci-dessous…

\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
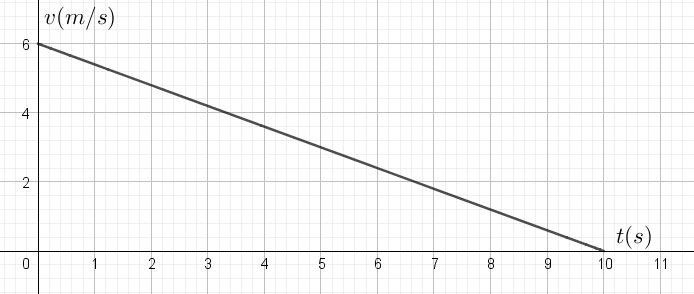
Graphe n°1:
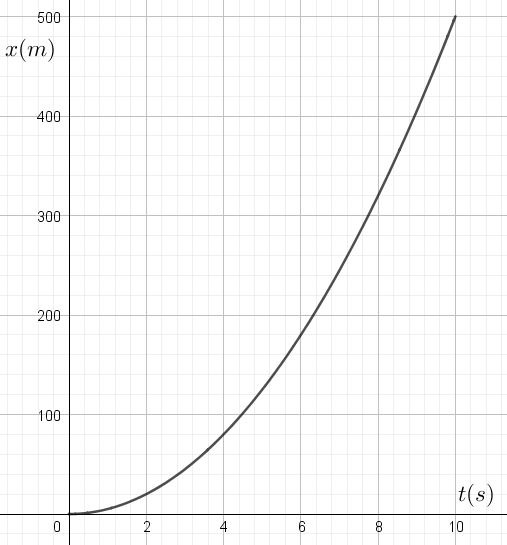
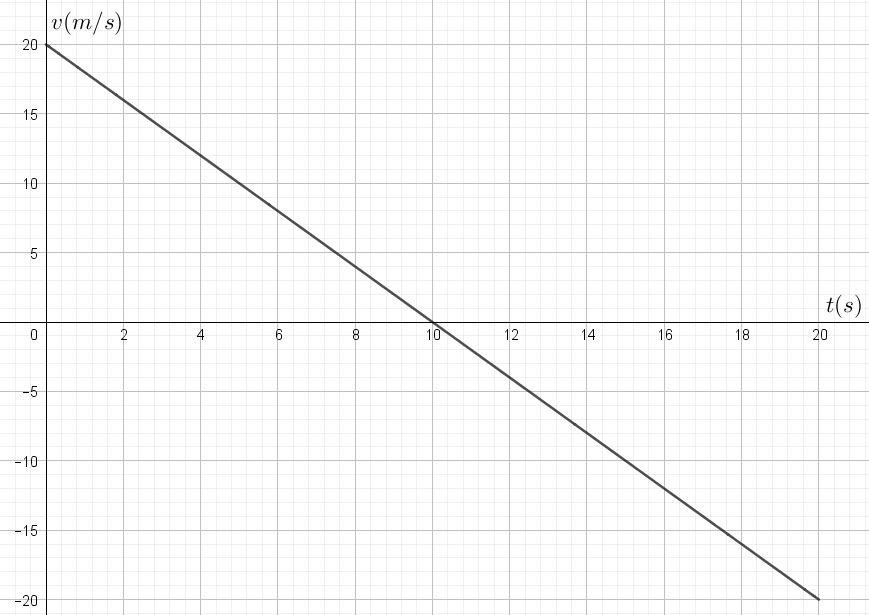
Graphe n°2:
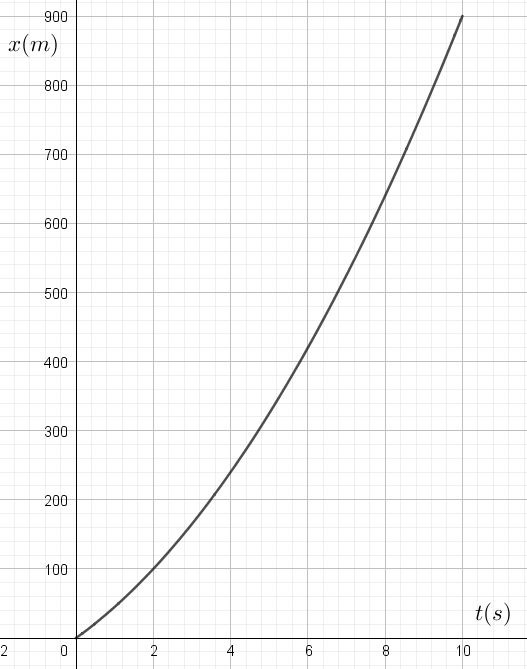
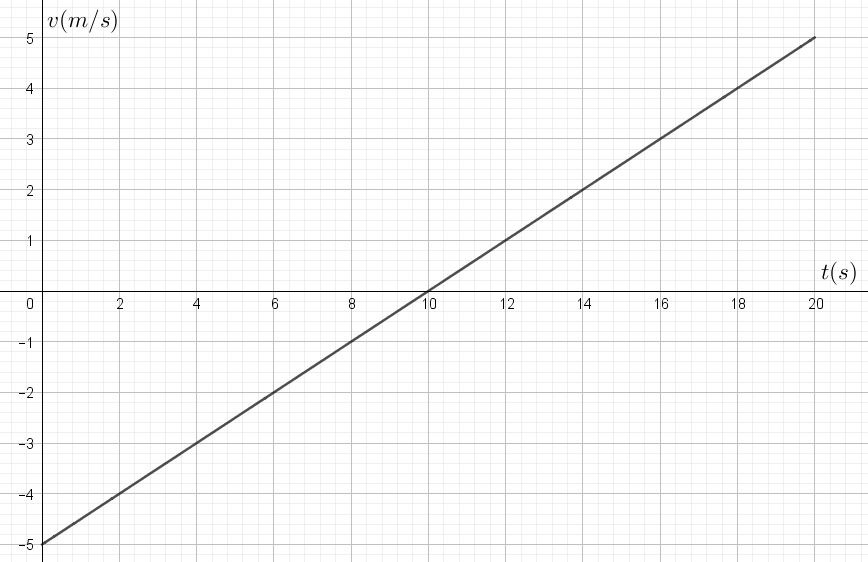
Graphe n°3:
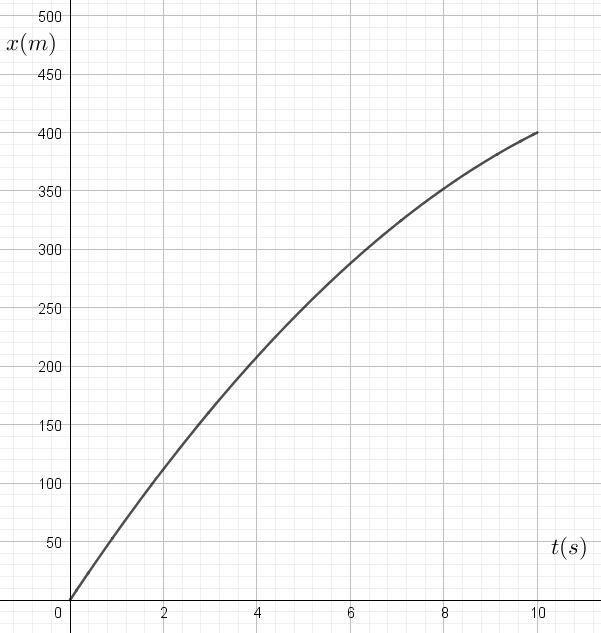
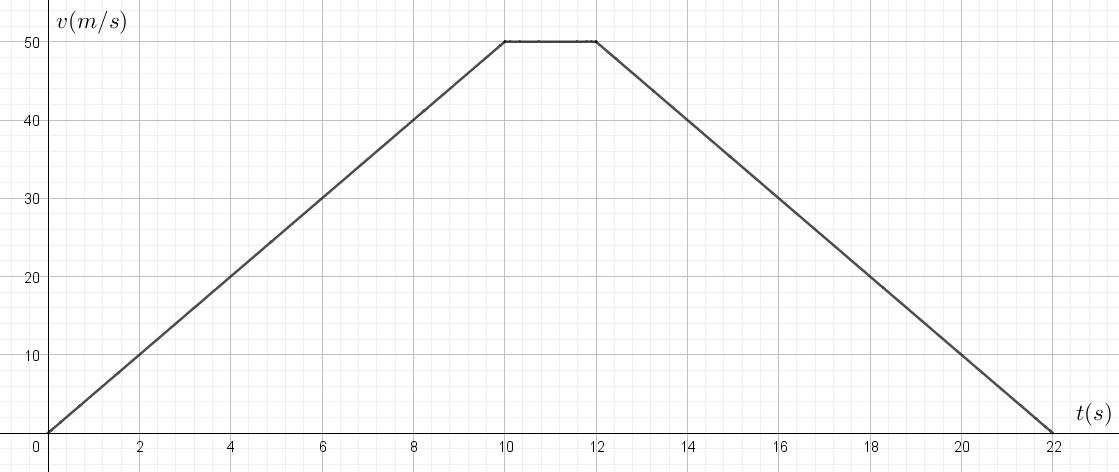
Graphe n°4:
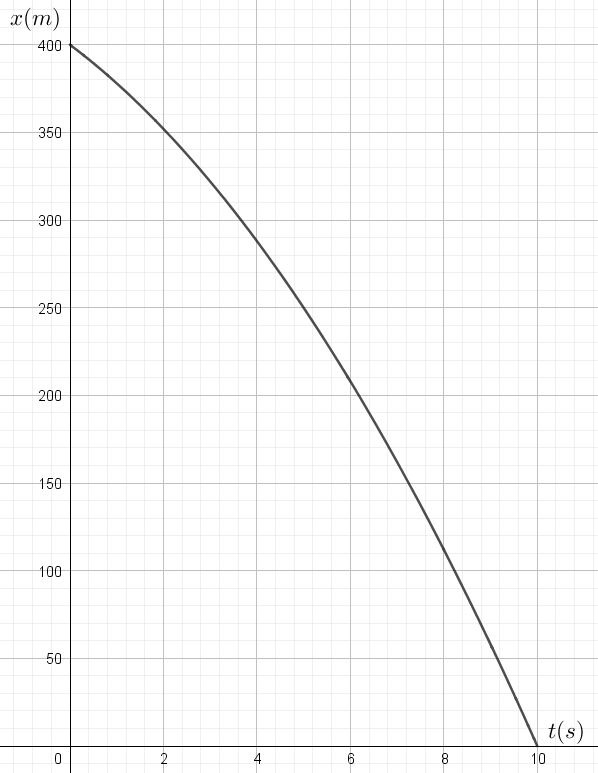
Graphe n°5:
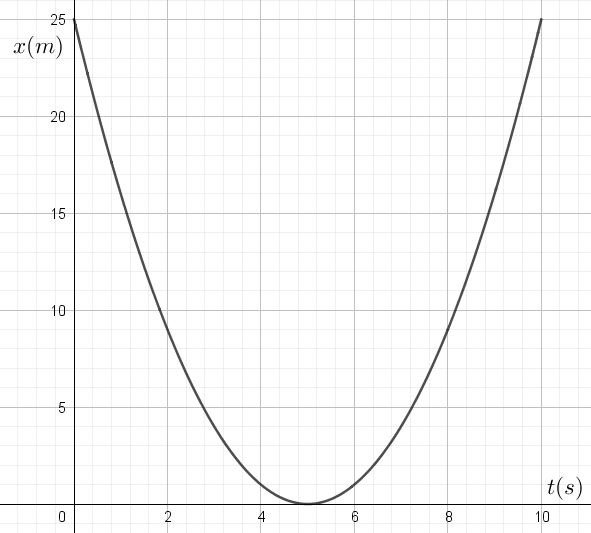
Graphe n°6:
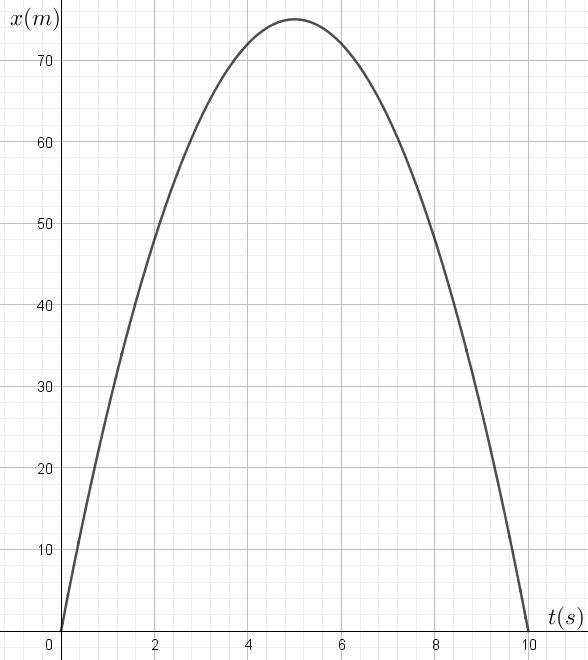
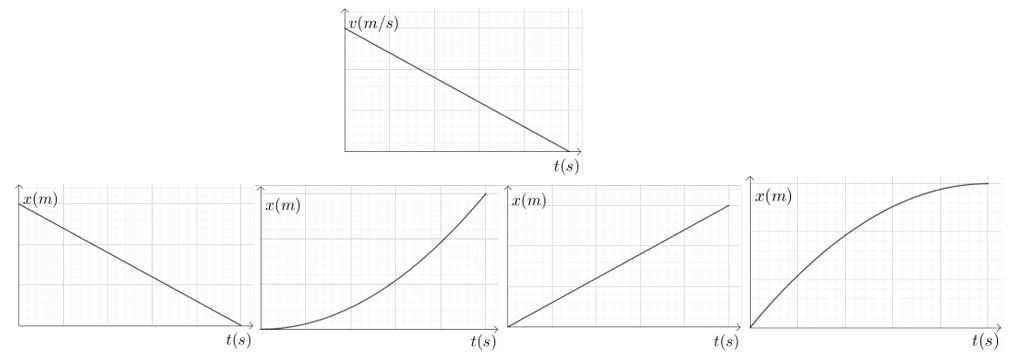
En réalité, les six graphiques que vous venez de caractériser correspondent aux équations suivantes. Est-ce cohérent avec ce que vous venez d’expliquer?
\(\\\)
\(\\\)
\(\\\)
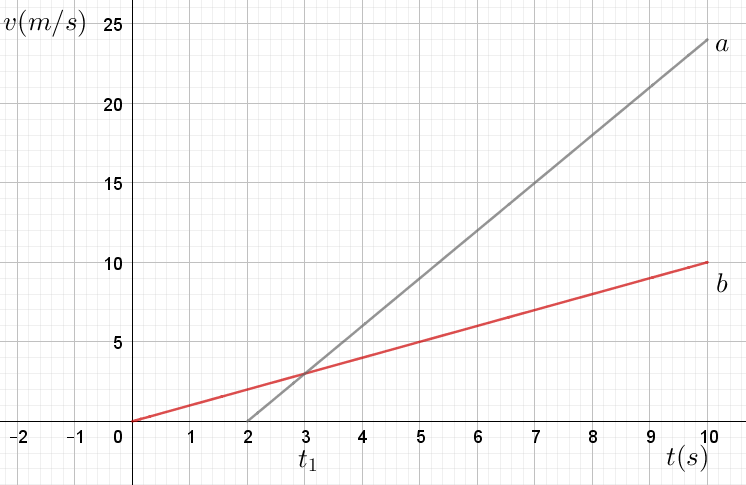
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
\(\\\)
Astuce: Durant le temps de réaction, les influx nerveux circulent dans le corps et le conducteur ne freine donc pas encore! Il est donc en MRU durant 0,7s avant d’entamer son MRUD!
\(\\\)

Détermine la valeur de la décélération de la voiture pour une vitesse initiale de 90 km/h.
\(\\\)
\(\\\)
\(\\\)
Astuce: On parle de deux mobiles, il faut donc écrire les équations de l’un \(x_{1}(t)\) et de l’autre \(x_{2}(t)\). Quand les deux véhicules occuperont la même position, on pourra écrire: \(x_{1}(t)=x_{2}(t)\)
\(\\\)
\(\\\)
\(\\\)
Rmq : pour s’entrainer à acquérir tous les bons réflexes (signes des composantes scalaires des vecteurs vitesse et accélération), on mettra le chat dans le sens du référentiel et le chien dans le sens opposé.
\(\\\)
\(\\\)
Si tu sais faire cet exercice, tu es paré pour tout le reste! Il combine temps de réaction, vitesses opposées et retard! Bref, de quoi bien s’amuser!
\(\\\)
\(\\\)
Exercices corrigés pas à pas disponibles ici! Fascicule reprenant:
- 3 pages de synthèse sur TOUT ce qu’il faut ABSOLUMENT comprendre avant de se lancer tête baissée dans les exercices sur le MRUA (et de perdre son temps) !
- Les 29 exercices ci-dessus corrigés dans les moindres détails en 41 pages!
Bref, l’équivalent de plus de 10 heures de cours pour moins de 30€ !!!
Clique sur le bouton « Acheter » ci-dessous…

Voici un exemple d’exercice résolu dans ce document:

Voici le plan de l’article:
\(\\\)
Si tu es plus auditif que visuel, cette matière est également disponible sous format vidéo sur YouTube!
Que dit la définition?
Le travail d’une force traduit les échanges d’énergie qui s’opèrent sur un système en mouvement, d’un point A vers un point B.
Alors, soyons clairs, si vous voulez retenir cette définition par cœur, ça ne sert absolument à rien! Par contre, prenez le temps de la relire et de la comprendre. Que nous dit-elle? Qu’une force qui travaille, c’est une force qui opère des échanges d’énergie. Et des échanges d’énergie sur qui? Sur un système en mouvement.
OUch… Il nous faut donc bien comprendre la notion de système avant d’aller plus loin!
En dynamique, on travaille sur des masses ponctuelles. Quand on aborde un problème de façon énergétique (càd via les travaux des forces), on considère plutôt des systèmes qui sont parfois un ensemble de masses. Exemple!

En dynamique, on regarderait la masse ponctuelle de la pomme seule. Ici, on considère le système pomme-Terre et on regarde l’énergie qui lui est apportée ou reprise. C’est un cas de figure un peu particulier, on en reparlera quand on étudiera l’énergie potentielle gravifique dans un prochain chapitre!
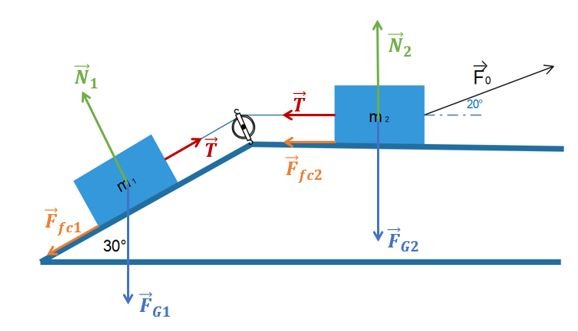
Dans ce cas, plusieurs systèmes sont envisageables:
dans ce cas, toutes les forces qui agissent sur la masse sont des forces externes.
dans ce cas, la force de tension devient une force interne, mais nous reparlerons de tout cela prochainement.
Quand on étudiera le travail d’une force, il nous faudra être très clair sur la force considérée ET le système sur lequel elle agit!
Il s’agit d’étudier le système « Wagon » pour lequel on souhaite un mouvement vers l’avant (de A vers B). Pour ce faire, 5 agents sont à l’œuvre.
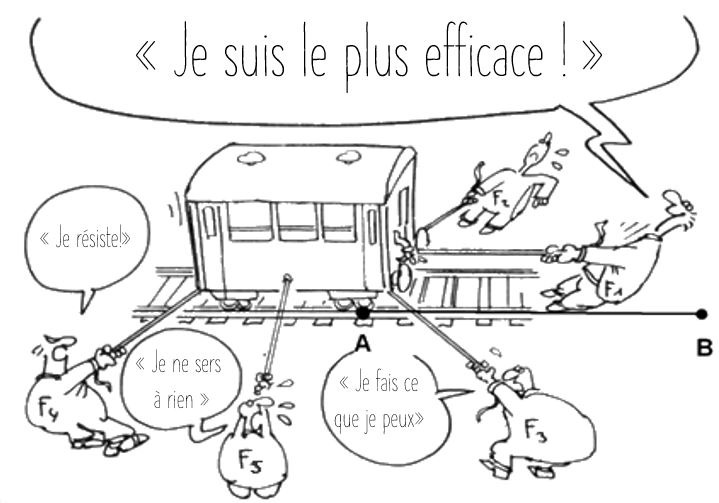
Ce superbe dessin ne m’appartient pas. Je le retrouve sur bien des sites de physique mais j’aimerais savoir qui l’a réellement dessiné! Bravo à lui (à elle), je l’adore, ce dessin!!
On vient de pressentir que la valeur de la force, si elle a de l’importance, n’est pas la seule à prendre en considération. Il faut aussi s’intéresser à la direction de cette dernière par rapport au déplacement du système.
Mini rappel, même! Si vous ne savez plus ça, vous êtes foutus!
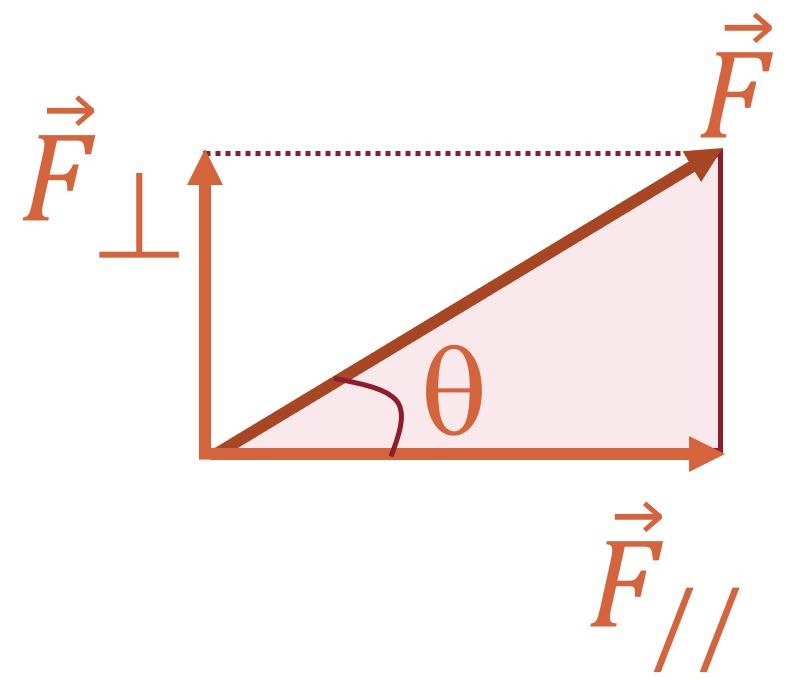
Un vecteur (force, ici) peut toujours être décomposé en deux composantes perpendiculaires: \(\overrightarrow{F_{//}}\) et \(\overrightarrow{F_{\perp}}\). On voit en effet que, si on ajoute le vecteur \(\overrightarrow{F_{\perp}}\) à la suite du vecteur \(\overrightarrow{F_{//}}\), on reforme le vecteur \(\overrightarrow{F}\).
\(\\\)
Mathématiquement parlant, on peut donc écrire:
\(\overrightarrow{F} = \overrightarrow{F_{//}} + \overrightarrow{F_{\perp}}\)
On peut donc, sans stress, travailler avec les deux composantes plutôt qu’avec le vecteur de départ.
\(\\\)
Si vous observez le triangle rectangle, vous pouvez y écrire la relation du cosinus. On obtient:
\(cos(\theta)=\frac{F_{//}}{F} \Leftrightarrow F_{//}=F.cos(\theta)\)
Ok, on garde ça bien au chaud, on y revient dans 35 secondes!
On a dit précédemment que c’est l’orientation de la force par rapport au déplacement qui permet de caractériser son efficacité. Regardons le schéma ci-dessous.
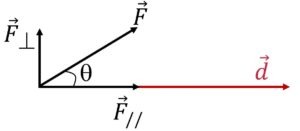
Imaginez que cette force agisse sur un système qui se déplace horizontalement vers la droite, le long du vecteur déplacement (noté \(\overrightarrow{d}\)).
On comprend aisément, que seule la composante \(\overrightarrow{F_{//}}\) de cette force participe au déplacement du système. On dira que, seule cette composante travaille.
La valeur du travail, càd la quantité d’énergie transférée au système dépend donc de la valeur de \({F_{//}}\), mais également de la distance sur laquelle cette force agira. On peut donc, en toute logique donner (enfin!) la relation mathématique du travail d’une force:
La relation mathématique qui définit le travail d’une force est:
\(\\\)
\(W_{F} \ = \ F.d.cos(\theta) \ = \ F_{//}.d\)Point de vue des unités, nous pouvons écrire:
\(J=N.m\)
Les Physiciens ont décidé de rendre hommage à James Prescott Joule (tout un programme), en renommant le Newtonmètre, le JOULE!
On a bien dit que le travail était une notion de transfert d’énergie, non? Quoi de plus normal que de l’exprimer dans cette unité!
\(\\\)
Une petite remarque: ne vous laissez pas influencer par ce qu’on dit dans la vie de tous les jours. Les étudiants ont souvent tendance à associer la notion de travail à celle de fatigue. Or, ce n’est pas toujours le cas. Le gars là, juste en-dessous, il a l’air de se fatiguer, mais en physique, pour autant qu’il garde son bras immobile, il ne travaille pas! Impitoyable physique…
\(\\\)

Le déplacement qui intervient dans la formule parait tout simple mais il peut poser problème dans le cas des corps déformables !
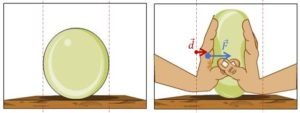
Observons ensemble le cas de figure ci-dessous. Chacune des deux mains exerce une force de 4N et déforme le ballon sur 1,5cm de chaque côté.
\(\\\)
\(\\\)
Dans un premier temps, on peut se dire que, étant donné que le ballon ne se déplace pas, il n’y a pas de travail. C’est faux! En réalité, il y a un détail de toute importance:
Le déplacement dont on parle est celui du point d’application de la force.
Or, on voit clairement (sur la deuxième représentation) que le point d’application de la force appliquée par la main gauche s’est déplacé de 1,5cm. Il y a donc effectivement un transfert d’énergie vers le système ballon. On peut même l’évaluer:
\(\\\)
\(W_{F_{main}}=F_{main}.d_{P.A.}.cos(\theta)=4 \ . \ 1,5.10^{-2} \ . \ cos(0°)= \ + 0,06 J \Rightarrow \) chaque main injecte une énergie de 0,06J dans la balle.
\(\\\)
J’imagine que vous avez remarqué que les \( \textbf{cm} \) ont été transformés en \( textbf{m} \); sans quoi le résultat final ne correspond pas à des Joules mais à du grand n’importe quoi!
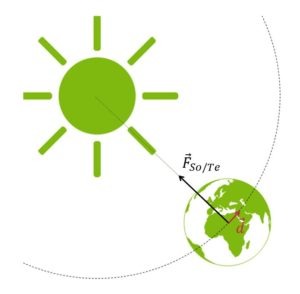
La force d’attraction gravitationnelle exercée pare le Soleil sur la Terre est responsable de la trajectoire circulaire de cette dernière. Le travail que cette force exerce sur le système Terre est-il positif, négatif ou nul?
On voit clairement que la force de gravitation exercée par le Soleil sur la Terre est perpendiculaire au déplacement de cette dernière. Dans ce cas de figure, la force gravitationnelle est donc incapable de transférer de l’énergie au système Terre. Le travail de la force gravifique est nul.
On tire sur la corde avec une force de 500N et un angle de 30° par rapport à l’horizontale. Un frottement de 100N agit entre le sol et le carton. Celui-ci se déplace de 3m vers la gauche. Après avoir identifié chacune des forces en présence, détermine le travail qu’elles exercent sur le système carton.
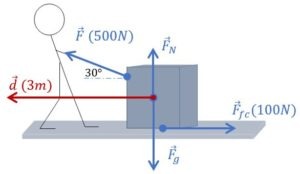
La première étape est la plus importante: il s’agit d’identifier les forces en présence. Si ce n’est pas évident pour toi, je te conseille de relire cet article.
\(\\\)
On a donc:
\(\\\)
On a également dessiné (dans une autre couleur, histoire de ne pas tout mélanger), le vecteur déplacement qui est horizontal et vers la gauche dans cet exercice. Il nous reste donc à appliquer la formule du travail d’une force à chacune des 4 forces en présence.
\(\\\)
Le travail total vaut \(W_{tot}= \ – \ 300 \ + \ 1299 \ \simeq \ + \ 1000 \ J\). Le système carton a gagné \(1000 \ J\) au cours de son glissement de 3m, sous l’influence des forces en présence.
- Un travail, c’est un transfert d’énergie (d’une force à un système)
- Une force qui ne déplace pas son point d’application ou une force qui agit perpendiculairement au déplacement, ne travaille pas.
- La direction avec laquelle la force agit par rapport au déplacement du système la rend plus ou moins efficace pour transférer de l’énergie.
- Un travail s’exprime en JOULE, càd en Newtonmètre.
\(\\\)
Dans un prochain article, nous étudierons le résultat d’un transfert d’énergie sur un système et nous parlerons d’énergie cinétique ou d’énergie potentielle.
N’hésitez pas à me laisser un commentaire, qu’il soit positif ou négatif, ou un pouce bleu si l’article vous a plu! Merci!
Il y a trois grandeurs intimement liées les unes aux autres qu’il te faut absolument comprendre:
Commençons avec le grandeur la plus simple: la différence de marche, notée \(\delta \) et définie par \(\delta = d_{2}-d_{1} \).
Pour faire simple, considérons deux sources transversales qui vibrent en phase (leur déphasage est nul et constant) à la surface de l’eau dans une cuve à ondes. Elles occupent donc les mêmes positions transversales aux mêmes instants. Quand une source est au sommet de sa trajectoire et s’apprête à descendre; la seconde est exactement dans le même état. Pour faire plus simple encore, considérons qu’à la date t=0; les deux sources se trouvent à leur position d’équilibre et qu’elles s’apprêtent à monter dans le sens du référentiel vertical et orienté vers le haut, appelé Y. Les deux sources vibrent en mouvement harmonique et leurs équations respectives sont données par:
\(y_{S1}(t)=A_{1}sin(2\pi ft)\)
\(y_{S2}(t)=A_{2}sin(2\pi ft)\)
On comprend aisément, en regardant la Fig.1 que la constante de phase \(\phi\) est nulle.
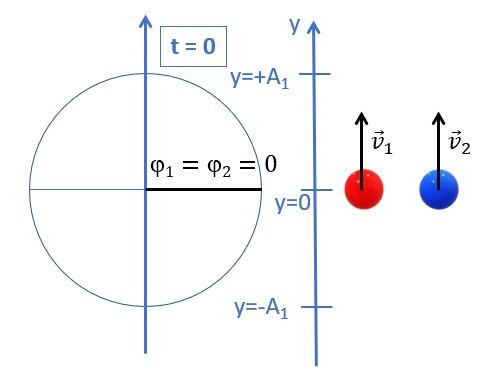
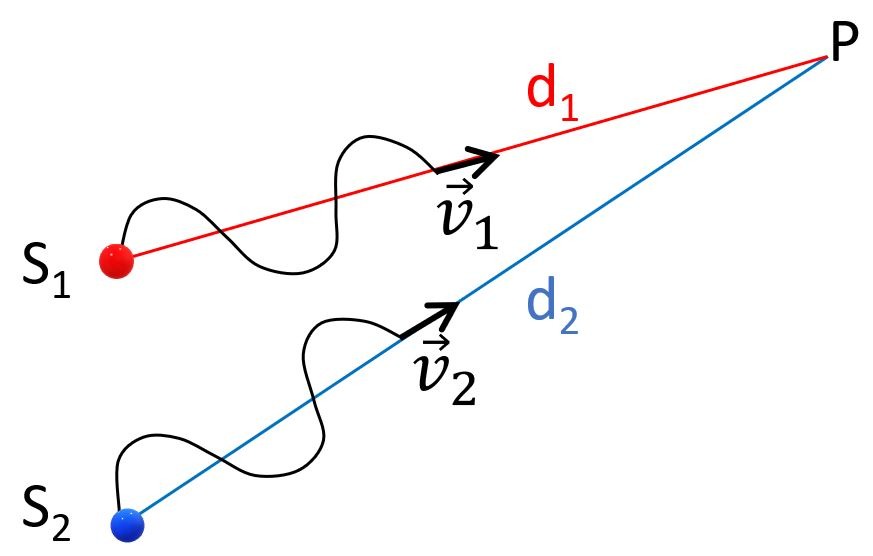
A l’instant t=0, on imagine que la surface de l’eau est plane et que le mouvement harmonique des sources commence seulement. Comme le montre la Fig.2, les deux sources vont générer des crêtes qui vont se propager à vitesse constante dans la cuve à ondes vers un point P quelconque.
Parce qu’on a considéré que la constante de phase des sources était nulle. Quand t=0, y=0 et la source monte, elle génère donc une crête.
La norme des deux vitesses est la même puisqu’il s’agit d’ondes de même nature qui se déplacent dans le même milieu.
Etant donné le point P choisi, on remarque que la distance \(d_{1}\) que doit parcourir l’onde issue de \(S_{1}\) est plus petite que la distance \(d_{2}\) que doit parcourir l’onde issue de \(S_{2}\) pour atteindre le point P en question. L’onde issue de \(S_{2}\) doit donc « marcher » sur une distance plus grande que l’onde issue de \(S_{1}\). De combien de mètres? D’une distance caractéristique, nommée différence de marche, et définie par \(\delta = d_{2}-d_{1} \).
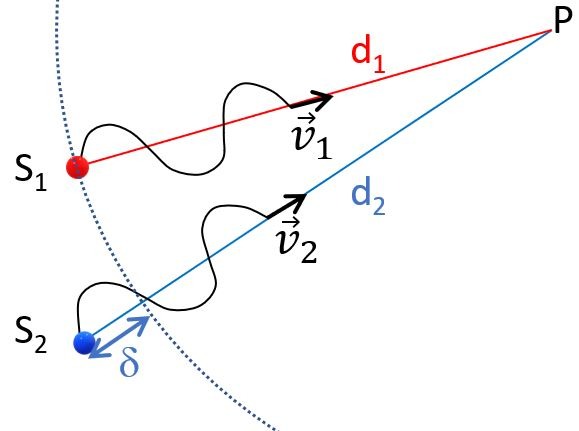
La première crête issue de \(S_{2}\) atteindra le point P plus tard que celle issue de \(S_{1}\). On pourra donc définir le retard \(\Delta t\) d’une onde par rapport à l’autre.
Prenons un outil mathématique: le graphique de l’élongation (càd de la position verticale) du point P au cours du temps. A la date t=0, ce point est à la surface d’une eau paisible et il ne bouge pas: y=0. Par contre, après un temps \(t_{1}\), il reçoit la crête issue de \(S_{1}\). Il se met donc à vibrer sous l’influence de cette 1ère onde.
Que se passe-t-il ensuite? La crête issue de \(S_{2}\) finit par arriver après un temps \(t_{2}\). A partir de cet instant, le point P reçoit deux ondes qui se superposent. On dit qu’elles interfèrent. Le point P vibre comme l’addition des deux ondes.
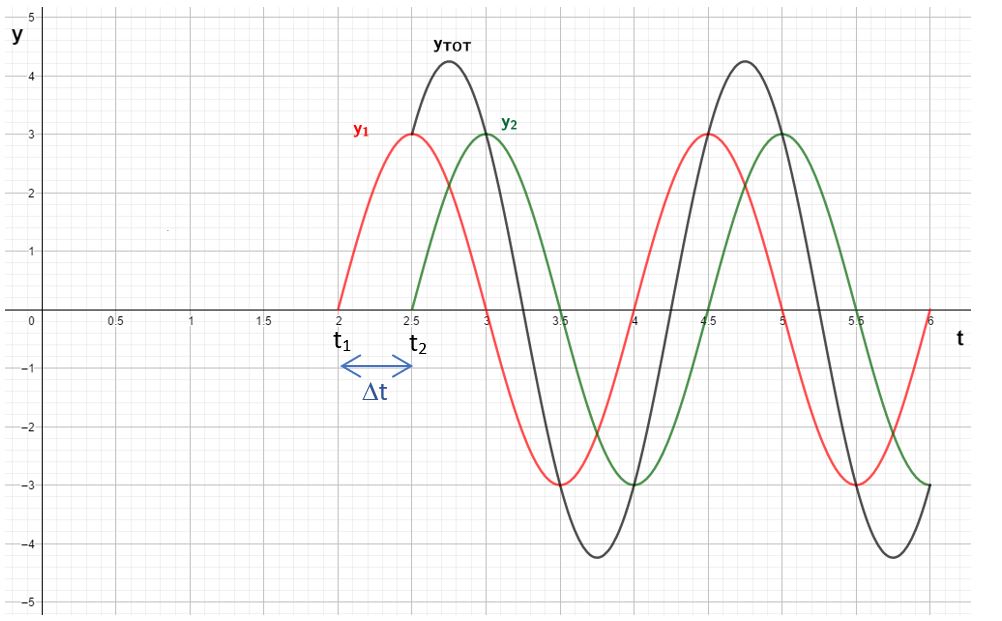
Puisque les ondes se baladent à vitesse constante, on peut définir leurs temps de parcours jusqu’au point P par:
\(t_{1}=\frac{d_{1}}{c}\)
\(t_{2}=\frac{d_{2}}{c}\)
Puisque \(d_{2}>d_{1}\), alors: \(t_{2}>t_{1}\) et le retard est donc défini par: \(\Delta t=t_{2}-t_{1}\)
Imaginons que le retard soit exactement égal à une période. Dans ce cas, le point P effectue une oscillation complète sous l’influence de la première source. Puis, lorsque la deuxième crête émise par \(S_{1}\) lui parvient, exactement à cet instant, arrive également la première crête en provenance de la deuxième source. On se retrouve donc avec deux crêtes qui se superposent exactement. Le point P vibre alors avec une amplitude double à chacune des sources. On parle d’interférence constructive.
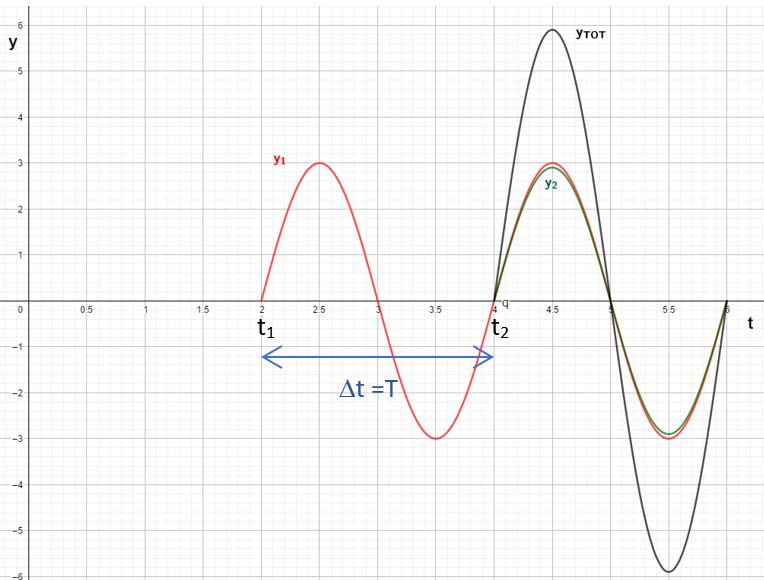
On devine facilement qu’il en sera de même si le retard vaut 2, 3 ou un nombre entier de périodes.
On obtient donc: Interférence constructive si \(\Delta t = kT\).
Par définition, une onde parcourt une longueur d’onde \(\lambda \) en une période \(T\). On écrit donc: \(\lambda = c.T\) où c est la célérité de l’onde.
Tu as reconnu la formule du MRU? Comme l’onde avance à vitesse constante, on peut dire que \(\Delta x = v.\Delta t\)
On ajoutera donc:
interférence constructive si \(\Delta t = kT\) ou si \(\delta = k\lambda\)
Imaginons que le retard soit exactement égal à une demi-période. Dans ce cas, le point P effectue une demi-oscillation sous l’influence de la première source. Puis, lorsque le creux émis par \(S_{1}\) lui parvient, exactement à cet instant, arrive également la première crête en provenance de la deuxième source. On se retrouve donc avec une crête et un creux qui se superposent exactement. Le point P ne vibre plus. On parle d’interférence destructive.
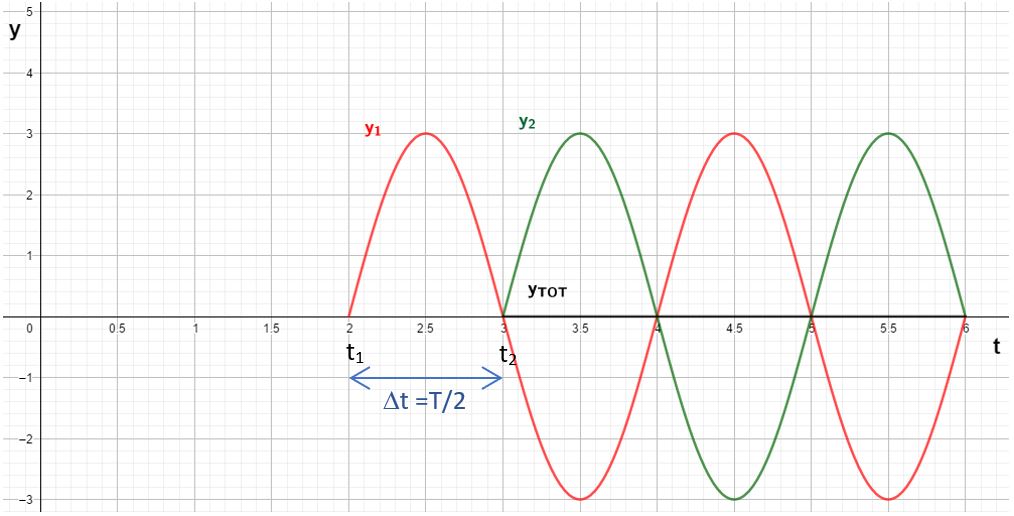
On devine facilement qu’il en sera de même si le retard vaut 3, 5 … ou un nombre impair de demi-périodes. En effet, un nombre pair de demi-périodes revient à un nombre entier de périodes. Vas relire le point précédent dans ce cas!
On obtient donc: Interférence destructive si \(\Delta t = (2k+1)\frac{T}{2}\).
On a toujours la définition: \(\lambda = c.T\)
Une onde parcourt alors une demi longueur d’onde en une demi-période. On ajoutera donc:
interférence destructive si \(\Delta t = (2k+1)\frac{T}{2}\) ou si \(\delta = (2k+1)\frac{\lambda}{2}\)
Observons le monde depuis le point P et regardons ce que les ondes nous amènent! Prenons les choses dans l’autre sens et commençons par étudier les interférences destructives.
Si le retard vaut une demi-période, la première source nous amène déjà un creux pendant que la seconde nous amène seulement sa première crête. Si on devait imaginer l’élongation du point P sous l’influence de chacune des deux ondes, on devrait dessiner ceci:
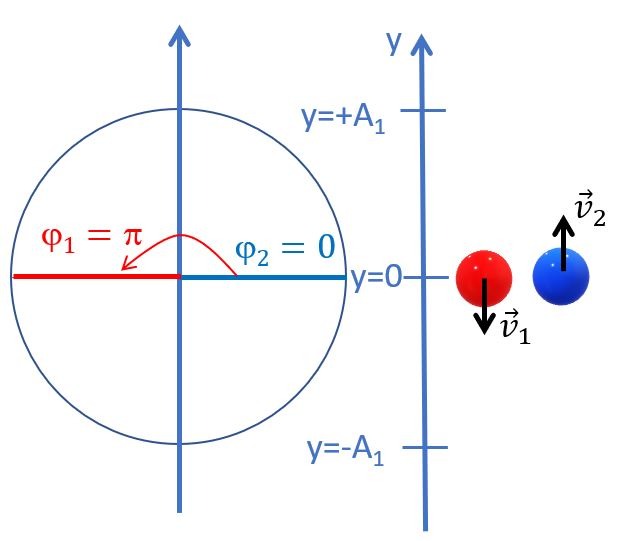
La première onde a une avance d’un demi cercle trigonométrique. Le déphasage entre les deux ondes vaut donc \(\Delta \Phi= |\phi_{2} – \phi_{1}| = \pi\).
Retenons qu’en une période (T):
Ayant ceci en tête, on pourra facilement se lancer à l’assaut de l’étude des couches minces, dans un prochain article! N’hésitez pas à me faire une critique constructive de mon travail dans l’espace « commentaires » ci-dessous ou tout simplement à liker si cet article vous a appris quelque chose. Merci!
A bientôt!
Dans cet article, je te montre 4 exercices différents qui sont typiquement rencontrés en physique dans l’étude du mouvement rectiligne uniformément accéléré. Si tu les comprends bien, tu n’auras pas de mal à reconnaitre le cas de figure dans lequel tu te trouves quand tu seras en interrogation (ou mieux encore en examen) sur le (très) célèbre MRUA! Remarque encore qu’on peut également parler de mouvement rectiligne uniformément décéléré: le non moins célèbre MRUD.
Avant toute chose, tu dois ABSOLUMENT comprendre ce qui suit. Prends le temps de le lire et de tout comprendre!
Précédemment, on a travaillé sur le MRU (ici très exactement) dont l’acronyme signifie: « Mouvement rectiligne uniforme ». Il y a deux mots importants là-dedans: RECTILIGNE et UNIFORME.
\(\\\)
Dans un MRU, le vecteur vitesse n’a donc pas le droit de changer: ni en direction, ni en intensité. Du coup, le vecteur accélération, défini par \(\overrightarrow{a}=\frac{\Delta\overrightarrow{v}}{\Delta t}\), est strictement NUL! Si tu rencontres un MRU, tu ne peux utiliser qu’UNE formule, celle-ci: \(v=\frac{\Delta x}{\Delta t}\), ou si tu l’exploses en tous ses termes: \(x(t)=x(0)+v.t\)
J’explique tout ça en détails ici!
Nous allons maintenant travailler le MRUA ou Mouvement RECTILIGNE « UNIFORMEMENT ACCELERE ». Ces deux derniers adjectifs vont ensemble, ne les dissocie pas.
Il y a donc deux choses importantes là-dedans aussi: RECTILIGNE et « UNIFORMEMENT ACCELERE ».
Dans un MRUA donc, le vecteur vitesse a le droit de changer, mais seulement en intensité. Du coup, le vecteur accélération, défini par \(\overrightarrow{a}=\frac{\Delta\overrightarrow{v}}{\Delta t}\) n’est PAS NUL et il est parallèle au vecteur \(\Delta \overrightarrow{v}\) (c’est toujours le cas) qui est lui-même parallèle au vecteur \(\overrightarrow{v}\) (parce que le mouvement est rectiligne). TU PEUX DONC (ce ne sera plus le cas dans les mouvements circulaires!!!) écrire la relation vectorielle de la variation de vitesse sous sa forme scalaire: \(\Delta v= v_{2}-v_{1}\).
Tu as maintenant le droit d’utiliser DEUX FORMULES:
Dans un premier temps, à chaque fois que tu écris cette relation, dis-toi ce que représente chaque terme:
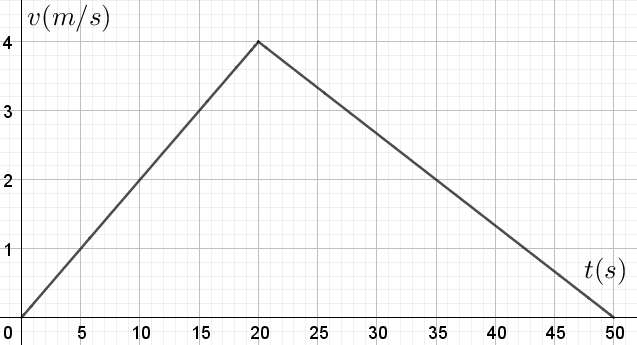
Le graphique ci-dessous représente 50 secondes du mouvement d’un objet. Calculez la distance totale parcourue. Déterminez l’accélération de l’objet.
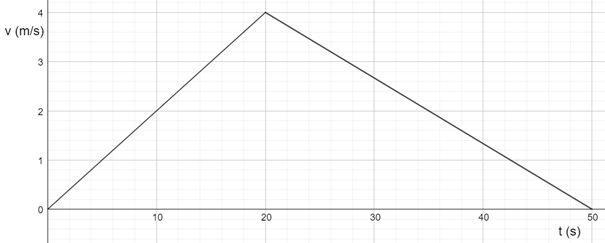
L’aire comprise sous le graphique horaire de la vitesse v(t), a les dimensions d’un espace \(\frac{[L]}{[T]}.[T]\), il donne le déplacement accompli \(\Delta x\).
Dans ce cas, il s’agit donc de calculer l’aire d’un triangle: \(\Delta x = \frac{B.H}{2} = \frac{50.4}{2} = 100 \, m\). On ne connait donc pas précisément la position de l’objet sur le référentiel X (càd la valeur de x), mais seulement le déplacement qu’il a accompli le long de ce référentiel. On sait qu’il s’est déplacé de 100m dans le sens du référentiel. On peut même dire, en séparant le graphique en deux triangles, qu’il a parcouru 40m en accélérant pendant 20s (\(\Delta x = \frac{B.H}{2} = \frac{20.4}{2} = 40 \, m\)), puis 60m en freinant pendant 30s (\(\Delta x = \frac{B.H}{2} = \frac{30.4}{2} = 60 \, m\)).
La valeur de l’accélération est donnée par sa définition: \(a=\frac{\Delta v}{\Delta t}\). Il s’agit donc simplement de déterminer la pente du graphique v(t). Rappelle-toi qu’en math, la pente du graphique y(x) est définie par \(m=\frac{\Delta y}{\Delta x}\). Ici, tu dois transposer tes connaissances: l’ordonnée y du mathématicien est remplacée par la vitesse v. Le \(\Delta y\) deviendra donc un \(\Delta v\). Les abscisses x du mathématicien sont remplacées par le temps t. Le \(\Delta x\) deviendra donc un \(\Delta t\). Au final, la pente \(\frac{\Delta y}{\Delta x}\) du mathématicien devient \(\frac{\Delta v}{\Delta t}\), càd l’accélération.
On remarquera que la vitesse étant positive, la première phase du mouvement est bien accélérée puisque v et a portent tous deux un signe positif; tandis que la seconde phase correspond à une décélération avec une vitesse positive et une accélération négative.
Calculez la distance de freinage d’un véhicule roulant à 140 km/h. On supposera que nous sommes dans des conditions normales, c’est-à-dire un temps de réaction de 1s et une décélération de 5 m/s².
Le temps de réaction du conducteur correspond au temps durant lequel le chauffeur se dit « OOPS, faut que je freine! », c’est un temps durant lequel les influx nerveux circulent. Le chauffeur se prépare à freiner, mais il ne freine pas encore; sa vitesse reste donc constante, il est en MRU! On sait donc que la voiture est en MRU pendant 1s; après quoi, le freinage commence et on passe en MRUD pendant un temps qu’on ne connait pas: le temps qu’il faut à la vitesse pour passer de 140 km/h à 0.
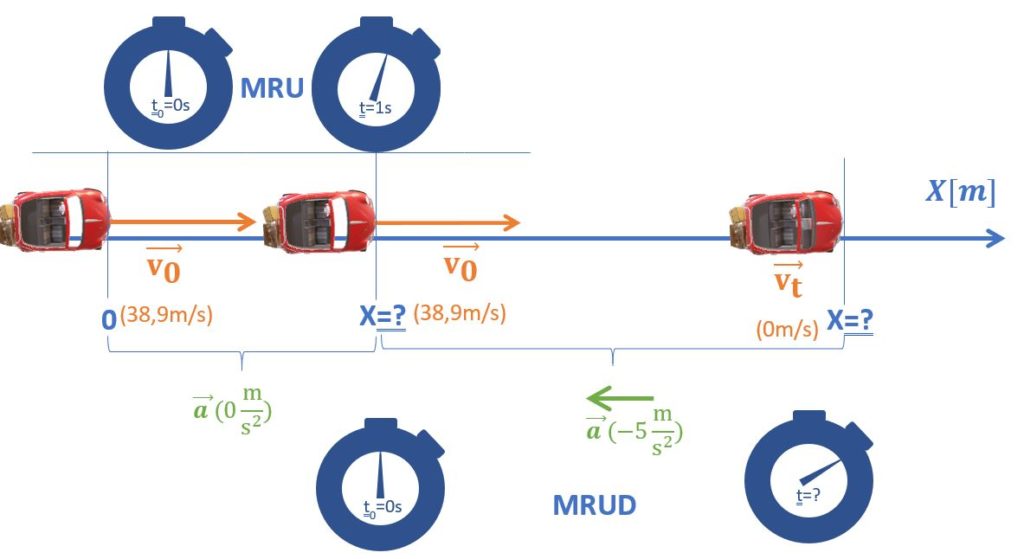
On peut donc tracer le tableau suivant:
| MRU | MRUD |
|---|---|
| \(\Delta t = 1s\) \(\Delta x = ?\) v=140km/h = 38,9 m/s | \(\Delta t = ?\) \(\Delta x = ?\) a = -5m/s² (signe opposé à la vitesse car mouvement décéléré) |
| En MRU, nous n'avons qu'une formule à notre disposition: \(\Delta x = v * \Delta t = 38,9 * 1 = 38,9 m\) | |
| Durant la phase de réaction, la position de la voiture passe de x=0 à x=38,9m. On peut donc compléter le schéma ci-dessus. Le freinage commence seulement maintenant. Remettons notre chrono à 0 et passons dans la colonne du MRUD. Attention, quand le MRUD commence, la position initiale de la voiture est donc x(0)=38,9m. | |
| En MRUD, nous avons deux formules à notre disposition: \(x(t)=x(0)+v(0)*t+\frac{a*t²}{2}\) \(v(t)=v(0)+a*t\) \(\\\) ou \(\\\) \(a=\frac {\Delta v}{\Delta t} \) |
|
| Ce qui donne: \(x(t)=38,9+38,9*t+\frac{-5*t²}{2}\) t représente le temps de freinage, càd le temps durant lequel la vitesse passe de 38,9m/s à 0. Nous ne le connaissons pas, mais la seconde formule nous permet de le calculer. \(\Delta t = \frac{\Delta v}{a}=\frac{0-38,9}{-5}=7,8 s\) |
|
| La phase de freinage dure donc 7,8s. Complétons la première formule: \(x(t)=38,9+38,9*7,8-\frac{5*7,8²}{2}\)=190m |
|
| La voiture parcourt donc 190m pour s'arrêter: presque 39m avant de freiner, puis 151m de freinage effectif. |
Le chauffeur d’un camion roulant à 120 km/h aperçoit soudain un obstacle à 50 mètres devant lui. Le temps de réflexe du chauffeur est de 0,7s et la décélération maximale de 8 m/s². Dans ces conditions, il ne peut pas éviter l’obstacle. Quelle sera, en km/h, la vitesse de collision ?
On remarque que cet exercice est similaire à l’exercice précédent; à la différence qu’une collision a lieu et que la vitesse finale du MRUD n’est donc pas nulle. Par contre, si on ne connait pas la vitesse finale, on connait sa position: elle a lieu à 50m de l’endroit auquel l’obstacle a été aperçu. Ceci nous permet de tracer le diagramme suivant:
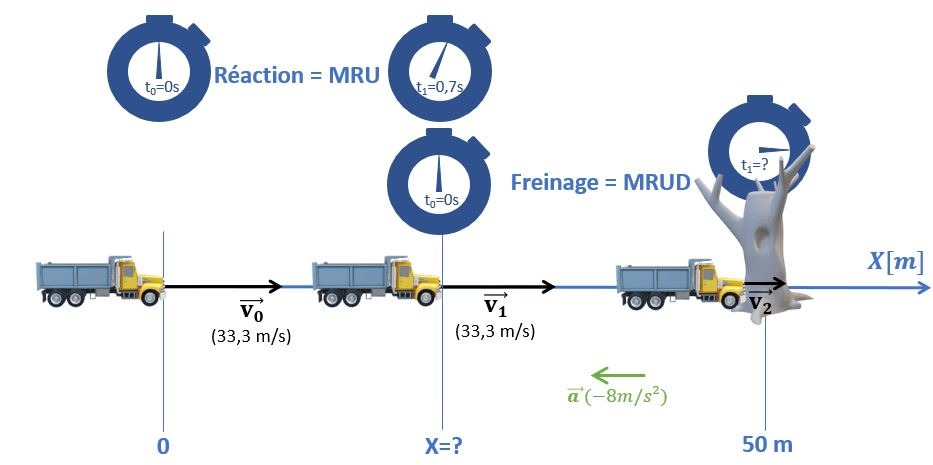
| MRU | MRUD |
|---|---|
| \(\Delta t = 0,7s\) \(\Delta x = ?\) v=120km/h = 33,3 m/s | \(\Delta t = ?\) x(t)=50m a = -8m/s² (signe opposé à la vitesse car mouvement décéléré) |
| En MRU, nous n'avons qu'une formule à notre disposition: \(\Delta x = v * \Delta t = 33,3 * 0,7 = 23,3 m\) | |
| Durant la phase de réaction, la position du camion passe de x=0 à x=23,3m. On peut donc compléter le schéma ci-dessus. Le freinage commence seulement maintenant. Remettons notre chrono à 0 et passons dans la colonne du MRUD. Attention, quand le MRUD commence, la position initiale du camion est donc x(0)=23,3m. | |
| En MRUD, nous avons deux formules à notre disposition: \(x(t)=x(0)+v(0)*t+\frac{a*t²}{2}\) \(v(t)=v(0)+a*t\) \(\\\) ou \(\\\) \(a=\frac {\Delta v}{\Delta t} \) |
|
| Ce qui donne: \(50=23,3+33,3*t+\frac{-8*t²}{2}\) t représente le temps de freinage, càd le temps durant lequel le camion passe de la position x=23,3m à la position x=50m. Remarquons que cette première formule est en réalité une équation du second degré à résoudre. Il suffit donc d'en calculer les racines pour trouver le temps après lequel la collision aura lieu. |
|
| Réécrivons l'équation sous sa forme canonique: \(\\\) \(4t² \ - \ 33,3t \ + \ 26,7 \ =\ 0\) \(\\\) \(\Delta = b² - 4ac = 33,3²-4*4*26,7=681,7\) \(\\\) \(t_{1}=\frac{-b- \sqrt{\Delta}}{2a}=\frac{+33,3- \sqrt{681,7}}{8}=0,9s \) \(t_{2}=\frac{-b+ \sqrt{\Delta}}{2a}=\frac{+33,3+ \sqrt{681,7}}{8}=7,4s\) |
|
| La collision a donc lieu après 0,9 s de freinage. L'équation de la vitesse nous permet d'évaluer sa valeur: \(v(t) \ = \ 33,3 \ - \ 8*0,9 \ = \ 26,1 \ m/s \ = \ 94 \ km/h\) |
|
| Le chauffeur réagit donc pendant 0,7s, puis freine pendant 0,9s. La collision a lieu à une vitesse de 94 km/h. |
Remarque importante: L’équation du second degré nous amène deux racines, càd deux temps possibles pour lesquels x=50m. Seule la première racine (\(t_{1}\)) est physiquement valable. La seconde correspond à un camion qui dépasse la position de l’obstacle (x>50m), avec une vitesse qui diminue à un rythme de 8m/s², au point de s’annuler (arrêt du camion), puis de devenir de plus en plus négative (retour en sens inverse avec une vitesse de plus en plus grande en valeur absolue). Il arrive donc un second instant (\(t_{2}\)) auquel la valeur de x prend une nouvelle fois la valeur 50m. Il est évident que cette racine n’a rien de physique, elle doit donc être rejetée.
\(\\\)
Un chien de chasse aperçoit, à 10m, un chat s’éloignant à la vitesse constante de 5m/s. Il démarre alors avec une accélération de 1,5 m/s². Calculer la durée nécessaire au chien pour rattraper le chat, la distance qu’il a dû parcourir et la vitesse atteinte.
Dans ce cas, il y a deux corps à étudier: le chien et le chat. Il nous faut donc doubler les équations et leur ajouter un indice pour éviter de s’emmêler les pinceaux. D’après l’énoncé, le chien est en MRUA (on peut donc écrire deux équations pour le chien) tandis que le chat court à vitesse constante (une seule équation donc pour ce chat).
Voilà la situation:
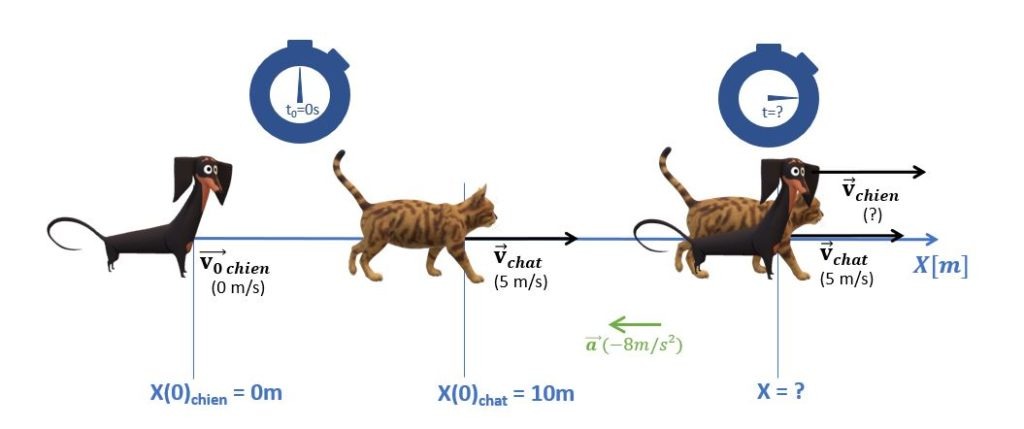
| Chat - MRU | Chien - MRUA départ arrêté |
|---|---|
| \(x_{chat}(0) = 10 m\) \(v_{chat} = 5 m/s\) | \(x_{chien}(0) = 0 m\) \(v_{chien}(0) = 0 m/s\) \(a_{chien} = 1,5 m/s²\) MRUA, a et v portent donc le même signe + |
| MRU, une seule formule à notre disposition: \(\Delta x = v \Delta t\) ou \(x(t)=x(0)+vt\) | MRUA: deux formules à notre disposition: \(x_{chien}(t) = x_{chien}(0)+v_{chien}(0)t+\frac{at²}{2}\) \(v_{chien}(t)=v_{chien}(0)+at\) |
| \(x_{chat}(t) = 10 + 5t\) \(\\\) Cette équation donne donc l'évolution de la position x(t) du chat au cours du temps. | \(x_{chien}(t)=0 + 0t+\frac{1,5t²}{2} = 0,75t²\) Cette équation donne l'évolution de la position x(t) du chien au cours du temps. \(\\\) \(v_{chien}(t)=0+1,5t\) Cette équation donne quant à elle l'évolution de la vitesse v(t) du chien au cours du temps. |
| L'énoncé nous dit que, à un instant t donné, le chien rattrappe le chat. A cet instant, ils occupent donc la même position et on peut exprimer que \(x_{chat}(t) = x_{chien}(t) \) | On peut donc écrire: \(x_{chat}(t) = x_{chien}(t) \) \( 10 + 5t = 0,75t² \) \(\\\) ou encore \(\\\) \( 0,75t² \ - \ 5t \ -10 \ = \ 0\) C'est une équation du second degré qui peut être résolue. |
| \(\Delta = b² - 4ac = (-5)²-4*0,75*(-10)=55\) \(\\\) \(t_{1}=\frac{-b- \sqrt{\Delta}}{2a}=\frac{+5- \sqrt{55}}{1,5} \ = \ -1,6s \) \(t_{2}=\frac{-b+ \sqrt{\Delta}}{2a}=\frac{+5+ \sqrt{55}}{1,5} \ = \ 8,3s\) |
|
| La racine négative est bien entendu à rejeter (un temps négatif n'a pas de sens). Le chien rattrape donc le chat après 8,3s de course. | |
| On demande également la distance parcourue par le chien en MRUA, il suffit donc d'évaluer l'équation suivante après 8,3s: \(x_{chien}(t)=0,75*8,3² = 51,7 m\) La position atteinte par le chien correspond évidemment à la distance parcourue puisque \(x_{chien}(0) = 0 m\) |
|
| Il nous reste à évaluer la vitesse atteinte par le chien après 8,3s d'accélération: \(v_{chien}(t)= 1,5*8,3 = 12,45 m/s = 44,8 km/h\) |
Et maintenant? On pourrait évidemment s’amuser à compliquer la situation en prenant deux objets en MRUA ou MRUD, se déplaçant l’un vers l’autre. L’un irait dans le sens du référentiel et l’autre dans le sens opposé. Je te propose un exercice ci-dessous. Je ne t’en donne pas la solution, mais tu peux me la demander par mail ou via l’espace des commentaires. Bon amusement!
A la date t=0, deux voitures A et B distantes de 200m se font face. La voiture A roulant à une vitesse constante de 80 km/h se met à accélérer à raison de 8m/s². La voiture B roulant à une vitesse de 110 km/h freine avec une décélération de 6m/s². Détermine l’instant du choc entre les deux voitures, l’endroit du choc et la vitesse de chacune des deux voitures à cet instant.
N’oublie pas qu’il n’y a rien de tel pour comprendre une matière scientifique, que de l’exercer via de nouveaux exercices! Je te propose ici, une liste de près de 30 exercices sur le MRUA , autant pour exercer ta compréhension des graphiques, que celle des équations (formules). Bon travail!
Comment exprimer mathématiquement le déplacement le long d’un référentiel X d’une onde sinusoïdale, ou encore, comment démontrer l’équation d’onde sinusoïdale progressive? C’est l’objet de cet article. Après le rappel d’un outil mathématique essentiel à comprendre, nous nous lancerons dans la (petite) démonstration de l’équation d’onde progressive.
Parce que la maitrise de cette équation vous conduira tout droit vers la compréhension des modes stationnaires qui expliquent, entre autres, la beauté de la physique à l’œuvre dans des instruments de musique.
Deux petites choses: une en math, l’autre en physique. Honneur aux mathématiques…
Imaginez une fonction mathématique pas trop compliquée: \(y(x)=2x^{2}\) dont voici le graphe.
\(\\\)
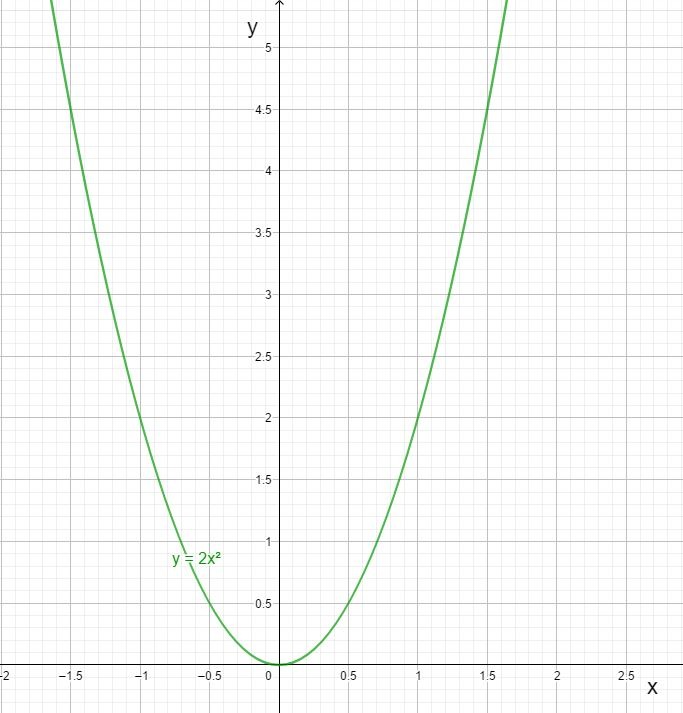
Le zéro de cette fonction est zéro, en effet: \(y(0)=0\).
Translatez maintenant ce graphique, disons de +1 unité vers la droite. Voici le graphe que vous obtenez: \(\\\)
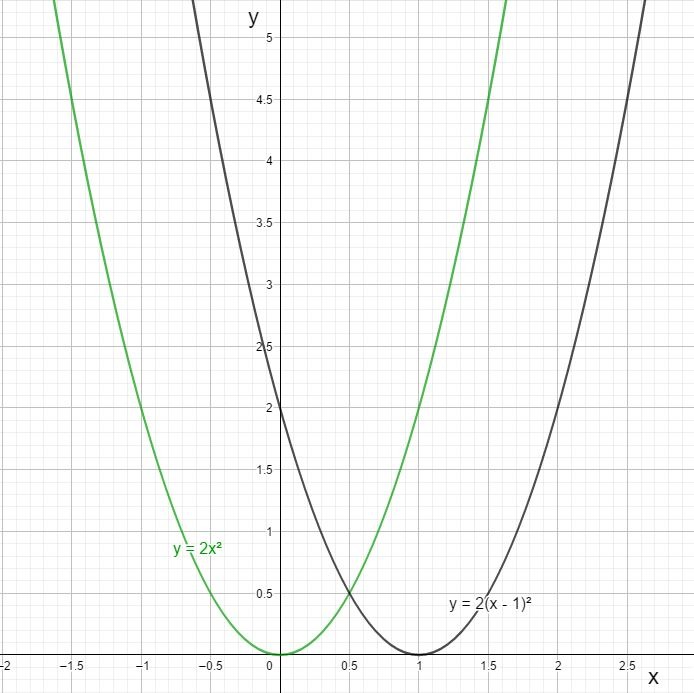
Le zéro n’est plus zéro, mais bien 1. La fonction \(y(x) = 2x^{2}\), devient: \(y(x) = 2(x-1)^2\). En effet, quand vous remplacez x par 1 \(\Rightarrow\) y vaut 0! Et ceci fonctionne pour n’importe quelle fonction!
Vous retenez donc ceci: si je veux faire glisser une fonction de +1 unité le long des abscisses, j’affecte l’abscisse de \( \ \) -1 \( \; \Rightarrow \;\) \(x \ \) devient \( \ (x-1)\)
Dans la démonstration qui suit, vous allez considérer une onde sinusoïdale qui se propage vers la droite dans une corde. Si les propriétés de la corde sont en tous points identiques, alors, l’onde se propage dans cette corde à vitesse constante. Concentrez-vous sur « la tête » de l’onde, vous allez voir un point qui avance en ligne droite à vitesse constante, exactement comme un mobile en MRU! Aaaahhhh, ce bon vieux MRU! Comme vous avez été drillé quand on a étudié le MRU ensemble, vous savez que:
Qui dit MRU, dit
\begin{equation}
\Delta x = v. \Delta t \\
\end{equation}
Eh bien, retenez ça aussi!
Enfin, par définition, la longueur d’onde (\(\lambda\)) est la distance que parcourt l’onde en une période (\(T\)). La période étant le temps nécessaire pour que la source ou n’importe quel point atteint par l’onde effectue un mouvement vertical d’aller-retour complet (\(0 \Rightarrow +A \Rightarrow 0 \Rightarrow -A \Rightarrow 0\)). Vous retiendrez donc enfin que:
\begin{equation}
\lambda = v. T \\
\end{equation}
Absolument pas! Suspendez le temps (en prenant une photo) et observez une onde qui se propage dans une corde, comme ceci:
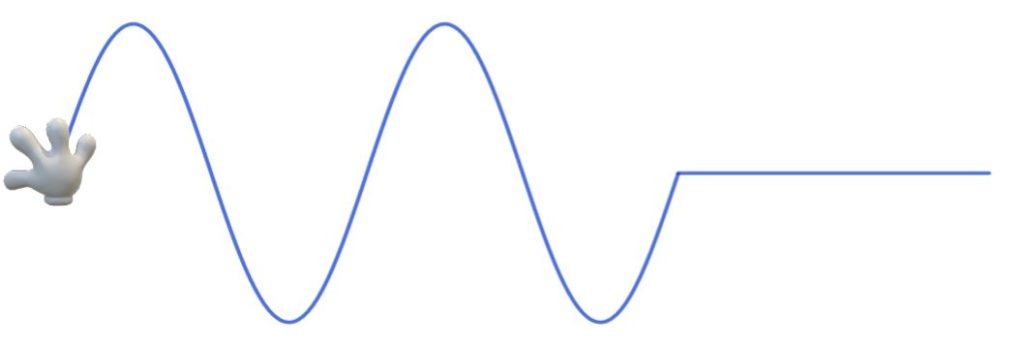
Si vous voulez étudier ce mouvement de l’onde, vous devez poser un référentiel. Or, l’onde avance en soulevant la corde transversalement, il nous faut donc étudier deux directions: la direction de propagation \(\Rightarrow\) X et la direction de déformation \(\Rightarrow\) Y.
\(\\\)
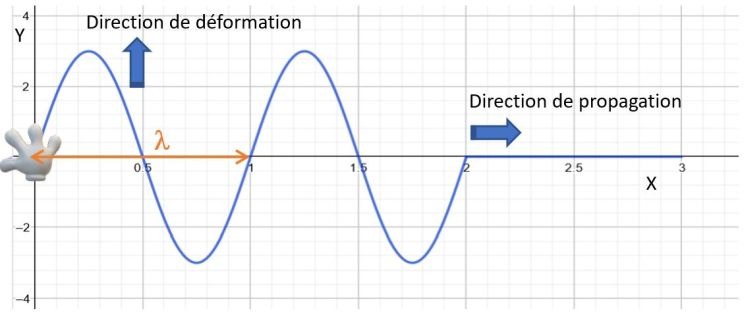
Comme vous gérez en math, vous reconnaissez de suite la fonction:
\begin{equation}
y(x)=A.sin(\frac{2 \pi}{\lambda}.x) \\
\end{equation}
Petite vérification: quand je remplace \(x\) par \(\frac{\lambda}{2}\), j’obtiens: \(y(\frac{\lambda}{2})=A.sin(\frac{2 \pi}{\lambda}.\frac{\lambda}{2})=A sin(\pi)\)=0. OK!
\(\\\)
Bon, vous avez suspendu le temps assez longtemps! Relancez la machine et contentez-vous de prendre une photo tous les quarts de période (\(\frac{T}{4}\)). Rappelez-vous que, par définition (2), l’onde avance d’une longueur d’onde en une période. Elle avance donc d’un quart de longueur d’onde en un quart de période. Voilà ce que vous devriez obtenir: \(\\\)
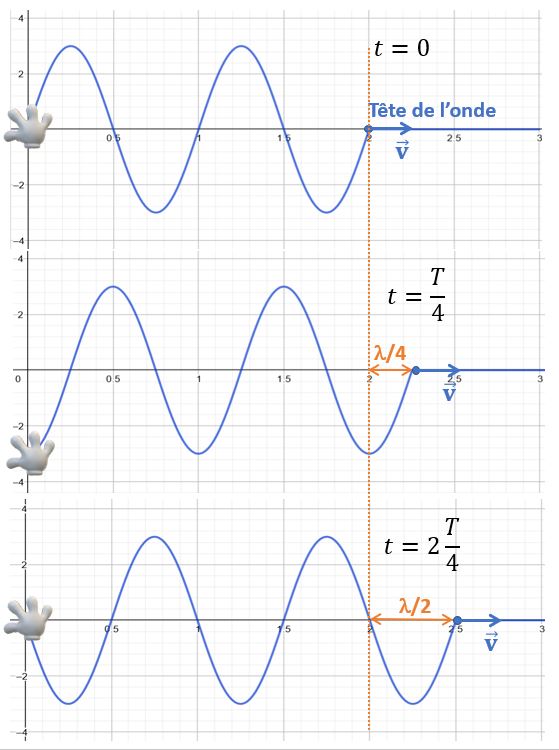
Si vous avez retenu le rappel de physique, vous ne me contredirez pas si je vous dis que pendant un temps \(t\), la tête de l’onde avance à vitesse constante d’une distance \(\Delta x = vt\). Ah, et donc, c’est juste la fonction \(y(x)=A.sin(\frac{2 \pi}{\lambda}.x)\) qui se translate vers la droite d’une distance \(\Delta x\) qui augmente avec le temps? Easy game! On l’a rappelé en début de cours, il suffit d’affecter l’abscisse de ce facteur \(\Delta x=vt\). Vous pouvez donc donner l’équation de cette onde sinusoïdale progressive!
\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}(x-vt)\right) \\
\end{align*}
En distribuant, on obtient:
\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{\lambda}vt\right) \\
\end{align*}
Or, par définition (2), on sait que \(v=\frac{\lambda}{T}\):
\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{\lambda}\frac{\lambda}{T}t\right) \\
&= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{T}t\right) \\
\end{align*}
On obtient finalement l’équation de l’onde progressive transversale sous la forme:
\begin{align}
y(x,t) \ = \ A \ sin\left(kx \ – \ \omega t\right) \\
\end{align}
où
Cette équation dépend à la fois de la position (x) dans la corde et du temps chrono (t) qui s’écoule.
Si vous voulez étudier un point de la corde et observer son oscillation transversale, fixez x à une valeur donnée. Prenons comme exemple \(x=\frac{\lambda}{4} \). Que fait ce point quand le temps s’écoule?
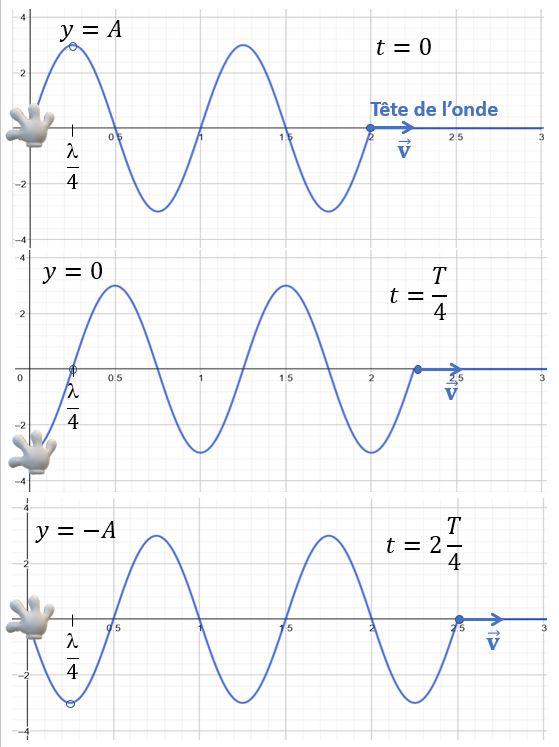
Vous voyez que l’élongation du point de la corde passe de \(y=A\) à \(y=0\), puis à \(y=-A\). On imagine facilement les points suivants: \( 0\) et \(+A\) après respectivement 3/4 de période et une période complète. Un point x de la corde reproduit fidèlement le mouvement périodique (harmonique) de la source qui a créé l’onde qui le traverse. On parle de périodicité dans le temps.
Vérifions le point \(x=\frac{\lambda}{4}\) à deux instants différents: \(t=\frac{T}{4}\) et \(t=\frac{T}{2}\). L’équation \((4)\) devient pour \(t=\frac{T}{4}\) :
\begin{align}
y(\frac{\lambda}{4},\frac{T}{4}) &= A \ sin\left(\frac{2 \pi}{\lambda}\frac{\lambda}{4} \ – \ \frac{2 \pi}{T}\frac{T}{4}\right) \\
&= A \ sin\left(\frac{\pi}{2} \ – \ \frac{\pi}{2}\right) \ = \ 0 \\
\end{align}
Et pour \(t=\frac{T}{2}\) :
\begin{align}
y(\frac{\lambda}{4},\frac{T}{2}) &= A \ sin\left(\frac{2 \pi}{\lambda}\frac{\lambda}{4} \ – \ \frac{2 \pi}{T}\frac{T}{2}\right) \\
&= A \ sin\left(\frac{\pi}{2} \ – \ \pi\right) \\
&= A \ sin\left( \ – \ \frac{\pi}{2} \right) \ = \ -A\\
\end{align}
Au lieu de fixer un point de la corde, fixons un temps en prenant une photo à un moment donné, soit \(t=0\).
On remarque alors que tous les points situés à une distance d’une longueur d’onde \(\lambda\) les uns des autres, oscillent en concordance de phase. Ils occupent la même élongation aux mêmes moments. Mathématiquement, ceci se traduit avec l’équation de l’onde progressive \((4)\) par:
Pour \(t=0\) :
\begin{align}
y(k\lambda,0) &= A \ sin\left(\frac{2 \pi}{\lambda} k \lambda \ – \ 0 \right) = A \ sin\left(k \ 2 \pi\right) = 0 \\
\end{align}
Il s’agit des points A, B et C repérés en orange dans la figure ci-dessous. Ils sont situés en positions respectives \(x=0\); \(x=\lambda\) et \(x=2\lambda\). Ils occupent la position transversale (le long de Y) d’équilibre et se préparent à descendre vers \(y=-A\). On parle de périodicité dans l’espace.
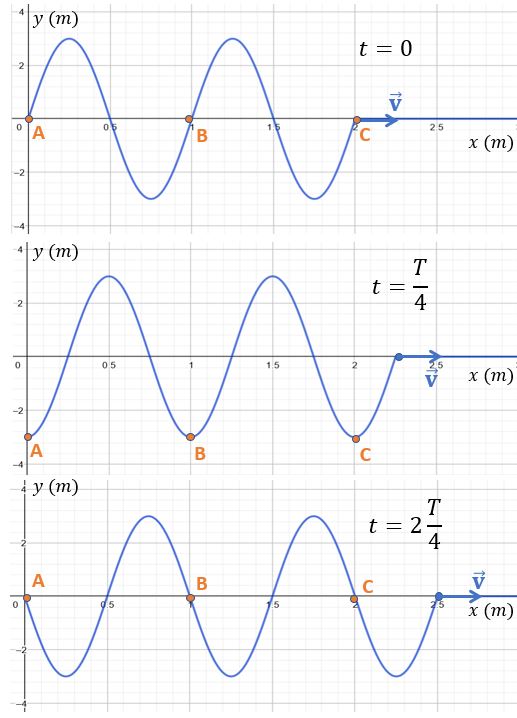
Vous devriez alors translater la fonction vers la gauche en affectant l’abscisse d’un terme positif. En recommençant le développement (ce qui peut être un bon exercice), vous devriez trouver l’équation d’une onde progressive caractérisée par:
\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}(x+vt)\right) \\
&= A \ sin\left(kx \ + \ \omega t\right) \\
\end{align*}
L’équation d’une onde transversale progressive se propageant dans le sens du référentiel x (généralement vers la droite), est donnée par:
\begin{align*}
y(x,t) &= A \ sin\left(kx \ – \ \omega t\right) \\
\end{align*}
\(\\\)
L’équation d’une onde transversale progressive se propageant dans le sens opposé au référentiel x (généralement vers la gauche), est donnée par:
\begin{align*}
y(x,t) &= A \ sin\left(kx \ + \ \omega t\right) \\
\end{align*}
avec
Afin de comprendre ces notions, je ne peux que vous conseiller de vous rendre sur l’excellent site d’animations de physique ostralo.net et de jouer avec l’onde tout en observant le comportement de la source et des différents points de la corde. N’hésitez pas à utiliser les curseurs (blancs) pour plus de clarté. J’exploite également cette animation dans une vidéo YouTube explicative. Bon amusement!
\(\\\) P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile ou s’il reste des zones nébuleuses dans l’article. Merci!
C’est une succession de photographies prises à intervalles de temps réguliers et superposées les unes aux autres. Concrètement, ça donne quelque chose comme ceci:
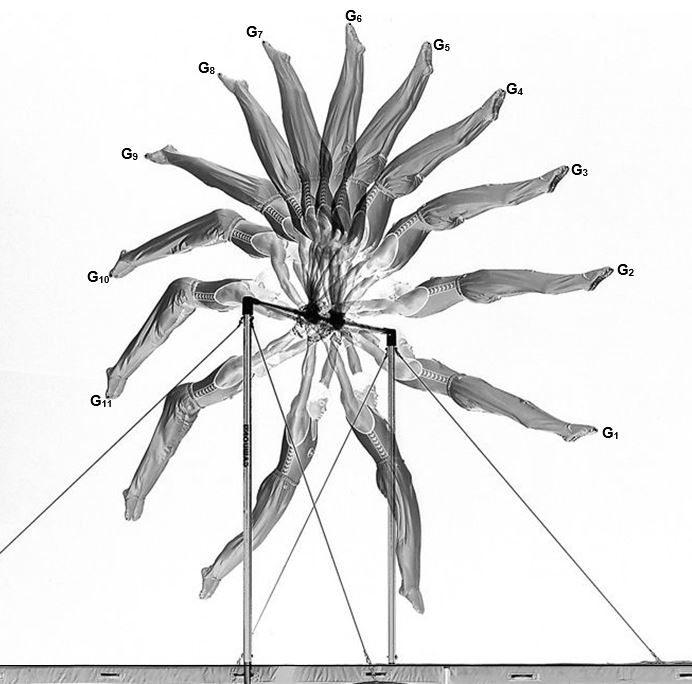
Les annotations sur le bout des pieds permet de voir que le mouvement se fait dans le sens anti-horloger. \(\\\)
L’intervalle de temps compris entre deux positions successives, s’appelle la base de temps et se note \(\tau\). C’est un élément essentiel à l’interprétation de la photo, mais nous en reparlerons dans un instant.
Essayons de construire le vecteur vitesse à la position notée \(G_{6}\).
Bon oui, c’est peut-être bête, mais c’est important. C’est quoi encore, la définition du vecteur vitesse instantanée?
\begin{equation}
\ \overrightarrow{v} = \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{r}}{\Delta t_{ }}
\end{equation}
Et je sais ce que vous vous dites: « Ah ouais, d’accord … et, on en fait quoi de cette définition??? »
Et bien, on la décortique! A quoi fait-elle appel? Au vecteur déplacement et à l’intervalle de temps.
\(\\\)
Sauf qu’il y a ce petit truc en plus: « \(\lim\limits_{\Delta t \rightarrow 0}\) ».
\(\\\)
Bon, okay, c’est une notion théorique de mathématicien … ouais, je sais, ça ne donne pas envie …
Mais bon, concrètement, ça donne quoi? Parce que la théorie, c’est bien, mais la pratique, c’est mieux! Un intervalle de temps infiniment petit les amis, c’est impossible concrètement parlant! Il nous faut donc nous adapter et trouver le plus petit intervalle de temps possible d’après les données que nous avons en notre possession. OUCH! Allons voir les informations sur la chronophoto!
Il y a trois éléments essentiels:
Nous avons déjà repéré le sens du mouvement. La base de temps est de 150 ms. ATTENTION! Soyez certains de lire correctement les unités! En physique, la moitié des réponses se trouve dans les unités! \(\\\)Comment lit-on « ms »? \(\\\)
J’entends parfois des élèves dire « èm-és » …. ou, pire plus grave, « mètre-seconde »! Et là, on se rend compte une fois de plus que le fameux kilomètre-heure dont je vous ai parlé précédemment refait surface! Apprenez à maitriser les outils que vous utilisez, c’est important.
\(\\\)Que lisez-vous? Une base de temps! \(\\\)
On parle donc bien d’un TEMPS! et un temps, s’exprime (dans le système international) en seconde! « ms », ce n’est donc pas plus compliqué que « mm » pour exprimer des petites distances ou que « mg » pour exprimer des petites masses. « ms » signifie donc tout simplement « milliseconde », càd (écoutez le terme) millième de seconde.
Donc, un intervalle de temps de 150 millièmes de seconde sépare deux positions: \(\tau=0,150 s\). \(\\\)
Il nous reste à relever l’échelle de la figure qui est la suivante: \( 1 \ cm \ papier \leftrightarrow 0,25 m \) \(\\\)
Ici encore, il est important de bien comprendre de quoi on parle: dès que je mesure 1cm sur mon papier, il représente en réalité 25 cm!
Nous voulons caractériser la vitesse au point \(G_{6}\). Pour ce faire, la définition (1) nous demande de prélever un vecteur déplacement sur un intervalle de temps le plus petit possible. Dans un premier temps, on pourrait penser que cet intervalle de temps est de 150 ms, mais on a alors un problème.
\(\\\) Si on considère le vecteur déplacement dont l’origine est le point \(G_{5}\) et l’extrémité le point \(G_{6}\), appelons-le \(« \Delta \overrightarrow{r}_{56} »\), il s’effectue en 150ms. Toutefois le rapport \(\frac{\Delta \overrightarrow{r}_{56}}{\Delta t_{ }}\) correspondra à la vitesse que le gymnaste possédait avant le point \(G_{6}\)!
\(\\\) De façon similaire, le vecteur déplacement dont l’origine serait le point \(G_{6}\) et l’extrémité le point \(G_{7}\), appelons-le \(« \Delta \overrightarrow{r}_{67} »\), conduirait au rapport \(\frac{\Delta \overrightarrow{r}_{67}}{\Delta t_{ }}\) qui correspondrait à la vitesse que le gymnaste possède après le point \(G_{6}\)!
\(\\\)
La façon la plus précise que nous offre cette chronophotographie pour déterminer la vitesse du gymnaste au point \(G_{6}\) consiste alors à prendre le vecteur déplacement de part et d’autre de ce point, càd le vecteur dont l’origine est le point \(G_{5}\) et l’extrémité le point \(G_{7}\). Par convention, nous écrirons ce vecteur déplacement \(« \Delta \overrightarrow{r_{6}} »\), càd le vecteur variation de position de part et d’autre du point 6. Ce changement de position a lieu en deux intervalles de temps \(\tau \). On aura donc: \(\Delta t = 2.\tau \). C’est fondamental de bien le comprendre!
\(\\\)Choisissons un référentiel (X,Y) et traçons le vecteur \(\Delta \overrightarrow{r_{6}}\). Etant donné qu’il s’agit du premier exercice, nous traçons également les vecteurs \(\overrightarrow{r}_{5}\) et \(\overrightarrow{r}_{7}\). En réalité, ils sont inutiles puisque, quel que soit le référentiel choisi, le vecteur déplacement ira toujours de la première position à la seconde. (Pour rappel).
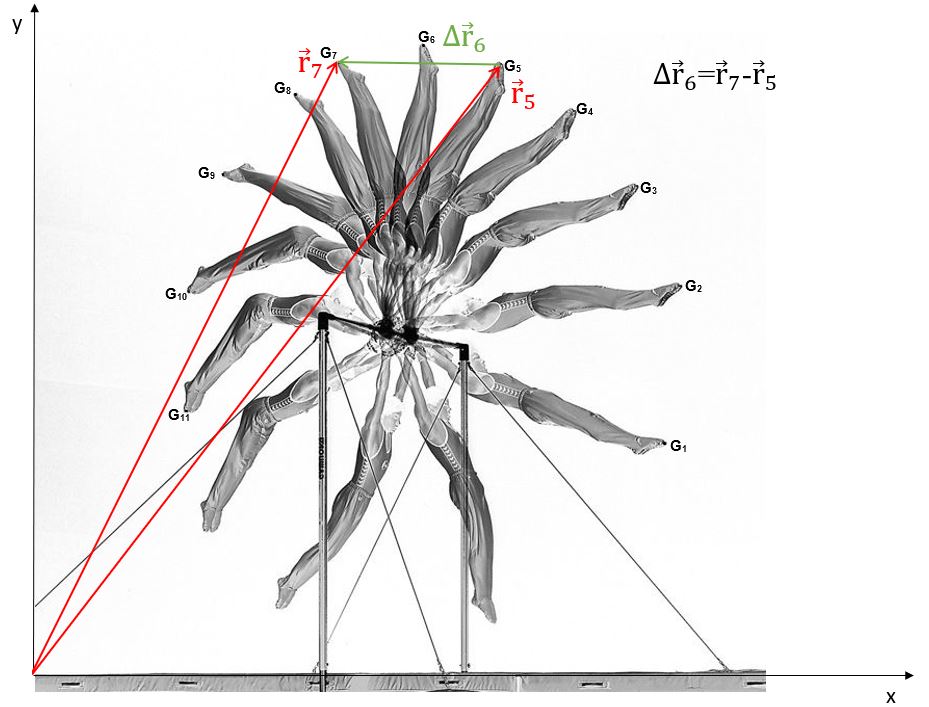
Le vecteur déplacement mesure exactement 4 cm sur papier. Toutefois, l’existence d’une échelle va nous obliger à faire des transferts entre « papier » et « réalité ». Le plus simple est, je pense, de réaliser un tableau comme le suivant:\(\\\)
| Sur papier | En réalité |
|---|---|
| \( \lVert \Delta \overrightarrow{r_{6}}\lVert \) = 4 cm | \( \lVert \Delta \overrightarrow{r_{6}}\lVert \) = 100 cm = 1m |
| \(\Delta t\) = 2 \(\tau\) = 300 ms = 0,3 s | |
| \( \lVert\overrightarrow{v_{6}}\lVert = \lVert\Delta\overrightarrow{r_{6}}\lVert / \Delta t = 1/0,3 = 3,3 m/s\) | |
| Nous devons donc représenter sur papier un vecteur vitesse dont la norme est de 3,3 m/s. Pour ce faire, nous allons choisir une échelle: 1 cm papier \(\leftrightarrow\) 1 m/s Nous devons donc tracer un vecteur vitesse de 3,3 cm de longueur. |
Nous connaissons maintenant la norme du vecteur vitesse au point \(G_{6}\) et nous savons qu’il a exactement la même direction et le même sens que le vecteur \(\Delta\overrightarrow{r_{6}}\) puisque \(\Delta t\) est un scalaire toujours positif. Il nous reste donc à dessiner ce vecteur dont le point d’application est \(G_{6}\).
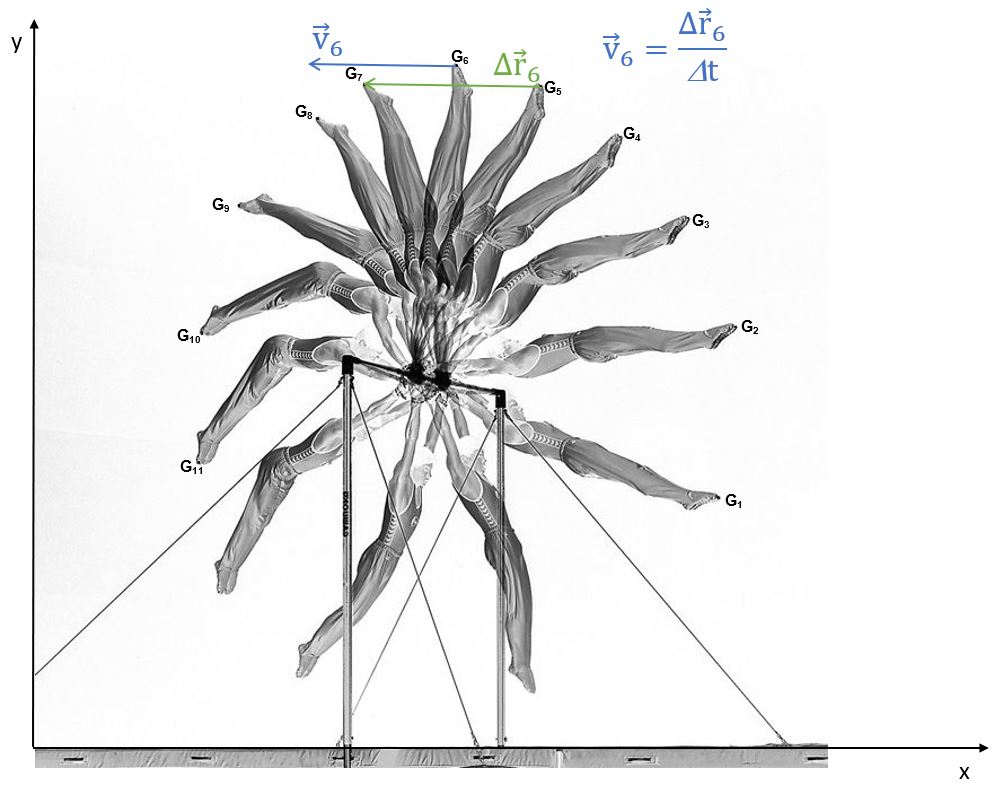
\(\\\)
IL Y A UN TRUC: \( \ \) afin de savoir si votre vecteur est cohérent, souvenez-vous qu’un vecteur vitesse (instantanée) est TOUJOURS tangent à la trajectoire! Si votre vecteur coupe la trajectoire, vous avez fait une erreur, cherchez-la!
\(\\\)
\(\\\)
P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile. Merci et à la prochaine!
Bonjour à toutes et à tous. Une fois n’est pas coutume, cet article participe à l’évènement « Quel élève étiez-vous, qu’est ce qui aurait pu faciliter votre apprentissage à l’école ou à la maison ? Des blogueurs reviennent sur leurs souvenirs d’écolier » du blog des-outils-pour-apprendre.com/. J’apprécie me balader sur ce blog. Deux articles ont dernièrement retenu mon attention, vous les retrouverez ici et ici!
Je suis enseignante depuis près de 15 ans, mais je n’oublie pas l’élève que j’ai été. Je pense que partager mon ressenti en tant qu’apprenant pourrait aider ceux d’entre vous qui doutent de leur potentiel.
Je suis née un 26 novembre. Peut-être n’est-ce pas la vraie raison, mais, dès l’école maternelle, on me dit que ce mois de l’année est responsable de mon manque de maturité intellectuelle. Je suis introvertie, j’éprouve beaucoup de difficultés à lire et à calculer, je déteste l’école. … Voilà mon portrait à l’aube de mes 10 ans.
Je suis née un 26 novembre, je suis titulaire d’une thèse en sciences physiques et je pars chaque matin, le cœur léger, enseigner la plus belle des sciences aux jeunes ados de mon lycée. Voilà qui je suis aujourd’hui.
Et entre les deux, que s’est-il passé ?
Comme je vous le disais, j’ai commencé dans le monde scolaire avec de grandes difficultés. Incapable d’apprendre au même rythme que les autres, on a envisagé de me faire recommencer une année de maternelle avant de me laisser entrer en primaire. Ce n’est donc pas des plus confiantes que j’ai démarré ma scolarité. Sans l’aide de ma mère et de mes sœurs ainées (des anges habitent ma maison), je n’aurais probablement jamais maitrisé la lecture. Quel gâchis quand on sait qu’un de mes plus grands plaisirs, est de lire ! Mais alors, quel élément déclencheur a pu me libérer de mes craintes ?
À l’école primaire, je me souviens des périodes d’évaluation durant lesquelles j’essayais de tricher sur ma voisine de classe. Je pleurais ensuite toute la récré parce que j’avais raté ! En réalité, mon travail ne se soldait pas toujours par un échec, mais par une cote tellement petite en comparaison du travail que j’avais investi… Ce scénario s’est répété de (trop) nombreuses fois. Mais un jour, mon institutrice a eu ces mots qui sont restés gravés en moi: « Tu vois qu’avoir confiance en soi donne de bons résultats ! ». Un ange passe… Me voilà libérée de mes angoisses et lancée sur le chemin de la connaissance. Je fais mon entrée dans le secondaire sans stress. Je fais soudainement partie des « bons élèves ». Il ne me manque qu’une carte : celle de l’audace ! Je ne parviens toujours pas à être sûre de moi. Il m’arrive souvent d’effacer la réponse qui est pourtant la bonne.
Je termine mes études secondaires avec brio, mais au moment de choisir mes études supérieures; je n’ose pas me décider. J’adore les cours de mathématique et de physique. Ce sont les seuls cours pendant lesquels je ne m’ennuie jamais. C’est donc tout naturellement, que le jour de la proclamation des résultats, à la question de mon professeur de sciences : « Et toi, Julie, que vas-tu faire l’année prochaine ? », je réponds : « Un bachelier en sciences physiques en Haute École ». Après une discussion avec ce professeur qui me rassure sur mes capacités ; j’ose une maitrise en sciences physiques à l’université. Pour la seconde fois en quelques années, un ange passe…
Me voilà donc à l’université… En dehors de la gestion de ma liberté qui n’est pas des plus réussies en première année, j’ai la chance de voir passer deux autres anges : deux amies de fac avec qui je passe de nombreuses heures à travailler ou à décompresser. Je termine ma maitrise et suis même invitée à faire une thèse de doctorat avec un séjour de 6 mois en Australie.
Si je fais le bilan de mon parcours scolaire, je suis convaincue que c’est la confiance qui a été la pierre angulaire de ma progression. Doucement mise en place par ma famille, puis par mes enseignants et enfin par mes amies, c’est elle qui a rendu possible l’impossible.
Du point de vue de l’enseignante que je suis devenue, en plus de la confiance, je pense que c’est le travail entre pairs qui porte l’élève. Contrairement aux spécialistes de la matière que nous sommes, les jeunes se situent plus ou moins au même niveau de leur apprentissage. Leurs questionnements sont donc essentiellement les mêmes. De ce fait, si tout le monde joue le jeu, si tout le monde travaille sérieusement sa matière, puis qu’une session de mise en commun est organisée, alors, c’est incroyablement rentable. Pourquoi ?
En conclusion, quelle est ma réponse à la question « Qu’est-ce qui facilite les apprentissages » ? Un travail sérieux, un petit noyau d’amis avec lesquels on révise (on parle donc bien de revoir la matière, pas de la découvrir), des rencontres adultes porteuses, le tout sur un fond de bienveillance et de confiance.
« Qu’est-ce qui empêche l’apprentissage ? » La peur de ne pas être capable, le manque de travail et l’isolement. Parce que, pour l’avoir vécu, je sais que le manque de confiance met l’élève dans un état de stress permanent et que, dans ces conditions, le simple fait de rester concentré en classe devient un challenge.
À l’heure actuelle, après 15 années d’enseignement et l’accompagnement de plusieurs centaines d’étudiants, je suis convaincue que presque n’importe qui peut apprendre presque n’importe quoi, pourvu qu’il se place dans de bonnes conditions : une écoute attentive en classe, un travail régulier et une collaboration entre pairs.
Je ne peux pas terminer cet article sans vous parler de Carol Dweck et vous conseiller la lecture de son excellent ouvrage « Osez réussir, changez d’état d’esprit » dont un résumé est disponible ici.
Dans ce livre, l’auteure nous explique à quel point l’état d’esprit est plus important que le talent. Et d’ailleurs, plus les années passent et plus je me dis que le génie n’existe pas, seule la passion amène l’Homme à se surpasser !
Si cet article te parle, laisse un pouce bleu, c’est une façon simple de savoir combien d’entre nous ont un jour été paralysés par la peur de ne pas être capable, alors qu’ils l’étaient ! Et bien entendu, sens-toi libre de laisser un commentaire si tu veux nous partager ta réflexion sur le sujet !