Bonjour à toutes et à tous,

Aujourd’hui, tu vas comprendre la force électrostatique via la loi de Coulomb. Comment? Et bien, d’abord, en se rappelant qu’on parle, comme pour toutes les forces, d’une bestiole vectorielle. Et donc, tu n’oublieras pas la technique de décomposition d’un vecteur, comme ici avec la force gravifique. Force gravifique, électrique ou vitesse, ce sont tous des vecteurs qu’on peut (qu’on doit souvent) décomposer. Et ensuite, en parvenant à faire parler en français la loi de Coulomb pour qu’elle te révèle vraiment ce qu’elle contient comme information!

I. L’électrisation

I.1. Une charge électrique, kesako?

La charge électrique se mesure en Coulomb (comme une masse se mesure en kilogramme), elle est portée par le très célèbre électron et par son, non moins connu acolyte, le proton!
Il te faut absolument (si si, j’insiste) connaitre la valeur de la charge élémentaire: \(1,602.10^{-19} C\)
Ce qui différencie le proton de l’électron, c’est le signe de la charge! Mais ça, tu le sais quand même…
Tu vois que le \(Coulomb \) est une unité vachement, vachement grande! \(1,602.10^{-19} C\), c’est (je ne l’écrirai qu’une fois): \(0,0000000000000000001602 C\)
\(\\\)
Il faut donc se lever tôt pour rassembler une charge de \(1C\) et en électrostatique, on parlera souvent de plus petites bestioles, que tu dois connaitre aussi, je suis vraiment désolée… Je te les présente, en commençant par une des plus petites:

1. Le femtocoulomb: \(1\ fC = 1.10^{-15}C\). C’est quand même vachement petit, on en parlera peu.
2. Le picocoulomb: \(1\ pC = 1.10^{-12}C\). C’est déjà mieux, tu risques de le rencontrer un jour ou l’autre.
3. Le très célèbre nanocoulomb: \(1\ nC = 1.10^{-9}C\). Bon, nano, tu entends 9, ça va, c’est pas trop compliqué à retenir!
4. Le plus célèbre encore microcoulomb: \(1\ µC = 1.10^{-6}C\). Ne l’oublie pas, celui-là!
5. Le quasi pas utilisé millicoulomb: \(1\ mC = 1.10^{-3}C\). C’est déjà trop gros, on s’arrête là!

Du coup, si tu mets dans un bol, \(3*100g\) de riz, tu as une masse résultante de \(300g\) de riz, c’est clair! Et bien, si tu rassembles 1 milliard (\(1.10^{9}\)) d’électrons, tu as une charge résultante (ou nette ou totale) de:
\(1.10^{9}*1,602.10^{-19}=1,602.10^{-10}C\)
On dira: la charge nette vaut \(q=1,602.10^{-10}C\)! Ah oui, je ne t’avais pas encore dit; si en physique, on attribue la lettre m pour la masse, on attribue la lettre q pour la charge!
\(\\\)
Bon, ok, et comment fait-on pour rassembler 1 milliard d’électrons? …. on frotte! Les physiciens parlent de tribologie. Du coup, quand le frottement engendre des transferts de charges (c’est l’objet du point suivant), on parle de triboélectrostatique! Tout un programme!

I.2.Rappel: la composition de la matière et la série triboélectrique

Pour comprendre les forces qui existent entre les atomes, il faut d’abord se souvenir de ce qu’est un atome, c’est évident. Je te propose deux objets: ta bouteille d’eau (super important d’hydrater ton cerveau quand tu bosses) et ton chat (si tu en as un, il est certainement occupé à se prélasser au soleil et à te montrer qu’il n’y a rien de mieux qu’une vie de chat… tant pis pour nous, ce sera pour une autre fois)!
Ces deux objets sont, par nature, électriquement neutres. Ils contiennent en effet autant de protons que d’électrons!
Que se passe-t-il si on frotte l’un contre l’autre? Pour répondre à cette question, il faut regarder la série triboélectrique: on voit que la fourrure de chat occupe une place supérieure à celle du PVC, qui est loin en bas, du côté des matières négatives.
\(\\\)

En frottant l’un contre l’autre, la fourrure deviendra positive et le PVC négatif. Autrement dit, c’est le chat qui cèdera, par frottement, des électrons (pas tous, hein) à la bouteille de PVC.

Et donc, le chat, ayant perdu des électrons, possède maintenant plus de protons que d’électrons: il développe une charge nette POSITIVE.
La bouteille de PVC gagne des électrons supplémentaires, elle a plus d’électrons que de protons: elle développe la même valeur de charge que le chat, mais NEGATIVE.
\(\\\)
Et donc, si on frottait une baguette de verre sur le chat, ça changerait quoi???
\(\\\)

C’est maintenant le verre qui est plus haut placé, c’est donc lui qui deviendra positif en cédant ses électrons au chat; qui devient négatif! Attention, j’espère que tu n’as pas parlé de transfert de protons! Les protons sont coincés dans le noyau, ils ne peuvent pas en sortir par simple frottement!!! Les protons ne se déplacent pas dans la matière!
\(\\\)

Bon, maintenant que l’on sait ce qu’est la charge et comment la créer, on va pouvoir s’amuser avec les charges!

II. Répulsion ou attraction?

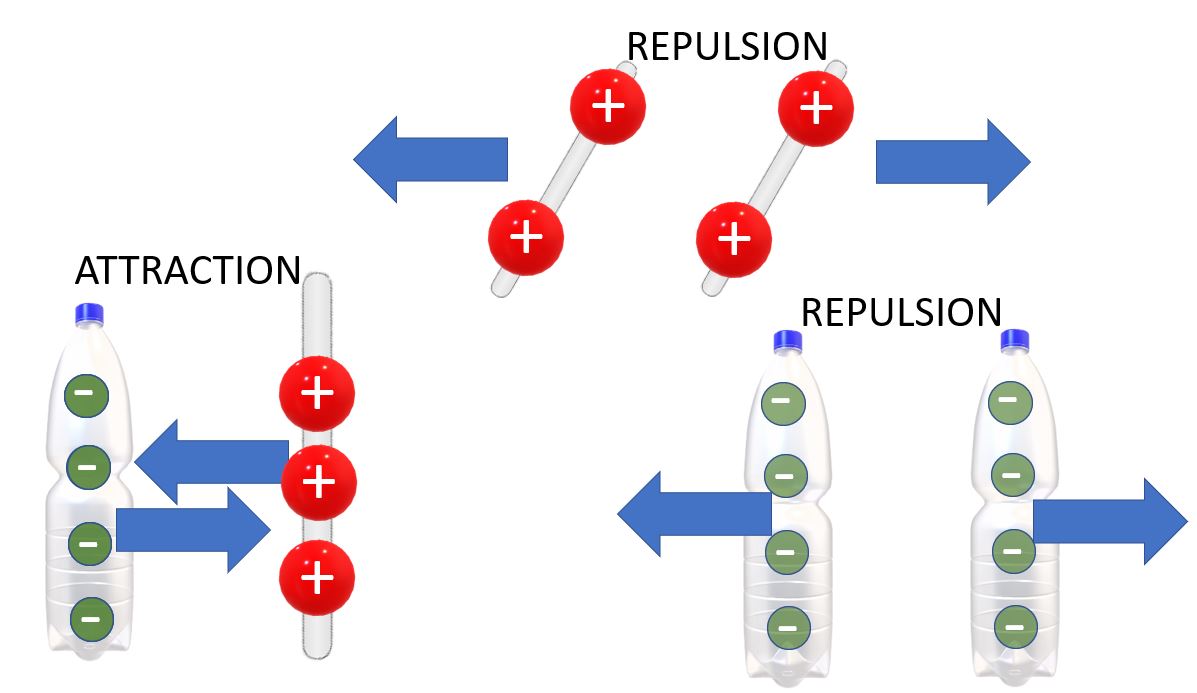
Alors, ça, pour le coup, tout le monde le sait: les opposés s’attirent! On vérifie donc par l’expérience que deux baguettes de verres, frottées contre un chat se repoussent! Deux charges positives se repoussent, en effet!
Que deux bouteilles de PVC, frottées contre un chat …. ben, se repoussent aussi, puisque deux charges négatives se repoussent!
Par contre, la baguette de verre est attirée par la bouteille de PVC et vice-versa! Enfin, pour autant qu’elles aient été toutes les deux frottées contre un chat!

III. La loi de Coulomb

III.1. LA formule

Il nous reste à évaluer ces forces en Newton! C’est Coulomb qui s’y est collé en 1785 et qui nous a sorti une belle petite formule que voici! Je te fais grâce de l’explication de sa technique expérimentale, mais si elle t’intéresse, j’en parle ici!
\(\\\)

\(\\\)
Evidemment, avant de faire parler cette formule en français, il faut comprendre ses paramètres. On y rencontre:

1. La constante électrique \(\frac{1}{4\pi\epsilon_{0}}\) qui caractérise le milieu dans lequel les charges se rencontrent. La plupart du temps (99,9% du temps), ça se passe dans le vide ou dans l’air et là, la constante \(\frac{1}{4\pi\epsilon_{0}}\) vaut \(9.10^{9}\ Nm²/C²\) …euh… oui, l’unité est un peu imbuvable, je te l’accorde… Retiens juste la valeur et dis-toi que tu dois exprimer les charges en Coulomb (même si on te parle de picocoulomb!) et les distances en Mètre!
2. La valeur absolue du produit de la 1ère charge \((q_{1})\) par la seconde charge \((q_{2})\). ATTENTION! N’oublie pas de prendre la valeur absolue, sinon, le signe du produit risque de te contrarier, puisqu’il ne correspond à rien!!!
3. Et enfin, la distance R entre les deux charges. N’oublie pas de l’exprimer en mètre! Vois également qu’elle intervient au carré \((R²)\). C’est une source d’erreur très fréquente: oublier d’appliquer le carré dans les calculs! C’est bête, mais ça arrive souvent! Ce carré signifie que si tu doubles la distance entre les deux charges, les forces de répulsion ou d’attraction qui existent entre elles sont divisées par 4! Ben oui, \(2²=4\)!

Bon, une dernière chose avant de faire parler cette formule! Remarque bien qu’elle est purement scalaire, ce qui veut dire que tu ne vois apparaitre de petite flèche nulle part! Pourtant, la force, c’est un vecteur! Cela signifie donc que Coulomb ne te renseigne QUE sur la valeur des forces, pas sur leur direction (chacun son job, hein!)! Pour la direction, tu traces une ligne imaginaire entre les deux charges, tu regardes leurs signes, puis tu traces les vecteurs Force: Répulsion ou Attraction?
\(\\\)

\(\\\)

III.2. Que nous dit la formule de Coulomb? En français?

J’ai pour habitude de dire que, si, à chaque fois que tu vois une formule en physique, tu prends le temps de la « lire » en français, alors, tu sauras toujours quand tu dois l’appliquer! Si on veut se la péter, on dira: « Je connais parfaitement le champ d’application de cette formule »! En bref, je sais faire mes exercices, quoi!
\(\\\)
DONC! QUE DIT COULOMB?

Il dit que (lis ce qui suit en regardant la formule de Coulomb, juste en-dessous):

• Si tu vois deux charges électriques: \(\large q_{1}\) et \(\large q_{2}\)
• dans le vide ou dans l’air:\(\large \frac{1}{4\pi\epsilon_{0}}=9.10^{9}\ Nm²/C²\)
• à une certaine distance l’une de l’autre: \(\large R\)

Tu sais que ces deux charges s’attirent (ou se repoussent) avec une force d’origine électrostatique, dont l’intensité est donnée par:
\(\\\)
\(\huge F=\frac{1}{4\pi\epsilon_{0}}\frac{\lvert q_{1}.q_{2}\rvert}{R^{2}}\)

III.3. Exemple!

Quelle force existe entre un proton et un électron d’un atome d’hydrogène, si on suppose (vaste blague, mais bon…) que l’électron subit une orbite circulaire (selon le modèle de Bohr) de rayon égal à \(0,53.10^{-10}m\)?

Que nous dit Coulomb, encore?

• Tu vois, dans cet énoncé, deux charges électriques: la charge de l’électron \(q_{1}=-1,602.10^{-19}C\) et la charge du proton \(q_{2}=+1,602.10^{-19}C\)
• dans le vide ou dans l’air: ben oui! On ne nous a pas dit qu’on avait coulé l’hydrogène dans de l’époxy!\(\frac{1}{4\pi\epsilon_{0}}=9.10^{9}\ Nm²/C²\)
• à une certaine distance l’une de l’autre: de fait, le rayon atomique de Bohr vaut \(R=0,53.10^{-10}m\)

Un électron et un proton ont des charges opposées, il s’agit donc de forces d’attraction.
L’intensité de chacune de ces forces est donnée par (Youhou! J’applique enfin Coulomb!):
\(\\\)
\(\large F=9.10^{9}\frac{\lvert (-1,602.10^{-19}).(+1,602.10^{-19})\rvert}{(0,53.10^{-10})^{2}}=8,2.10^{-8}N\)

Bon, ça peut paraitre petit comme force, mais n’oublie pas qu’on joue avec un électron et un proton dont les masses sont de \(9,11.10^{-31}kg\) et \(1,67.10^{-27}kg\) respectivement!
L’accélération qui en résulte est donc bien réelle!

\(\\\)

Conclusion

Tu es prêt à te mettre au travail! Prochain article, ce sera une série de quelques exercices progressifs qui concernent notre ami Coulomb! Bref, de quoi vraiment travailler!
\(\\\)