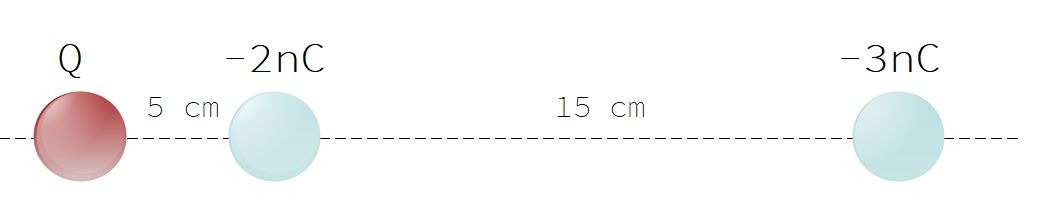Hello,
Aujourd’hui, je te propose une série de 4 exercices sur la force électrique (ou électrostatique, c’est encore mieux). Ils sont progressifs, et si tu t’efforces de comprendre chacune des étapes, tu verras que ce n’est pas si compliqué!
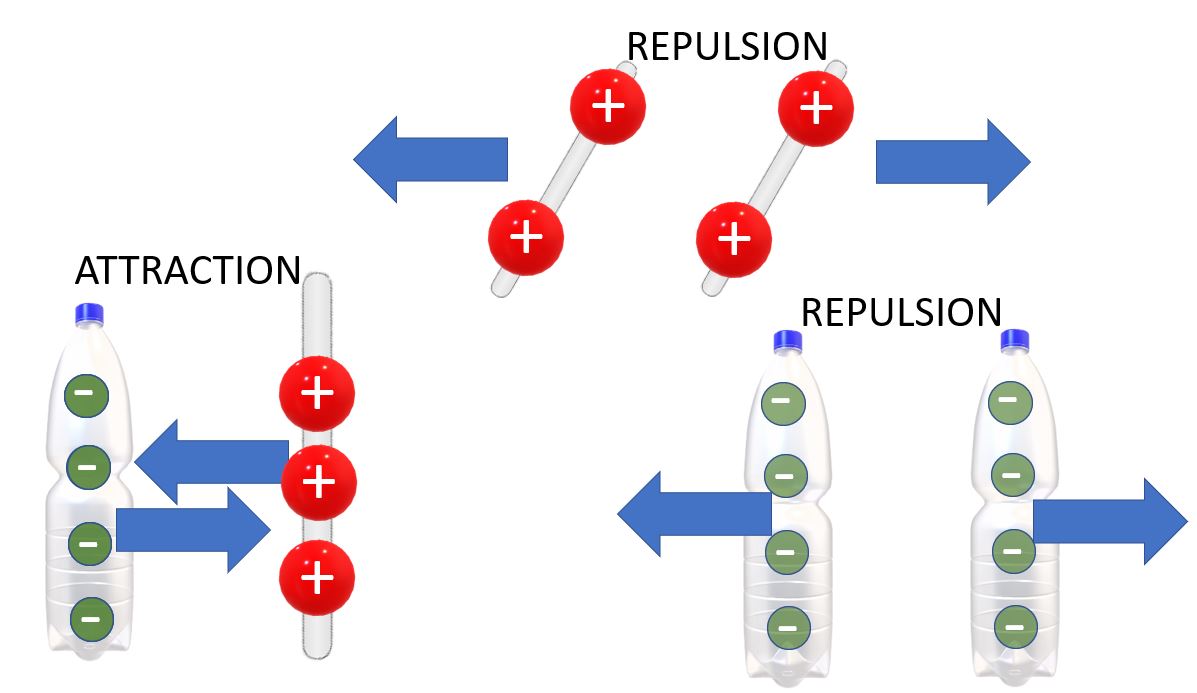
Avant de commencer, assure-toi que tu maitrises ce que je raconte ici! C’est un petit rappel de la théorie de la force électrique (loi de Coulomb)!
Exercice I: Calcul d’une force électrique entre deux charges
C’est le cas le plus simple, on l’a déjà rencontré dans l’article traitant de la théorie.
Enoncé Ex.1
La force électrique entre deux charges identiques est de 10N. Que devient cette force lorsque:
- La distance qui sépare les charges double?
- Une des deux charges double?
- Chacune des deux charges double?
- La distance qui sépare les charges est réduite d’un facteur 3?
Solution Ex.1
On nous parle donc clairement de deux charges électriques situées à une certaine distance l’une de l’autre. On peut donc, sans problème s’en référer à la loi de Coulomb. Par ailleurs, on ne nous parle pas de la direction des forces, mais uniquement de leur valeur (scalaire), on n’a donc pas besoin de s’embêter avec l’orientation des forces. On a:
\(\large F=9.10^{9}\frac{\lvert q_{1}.q_{2}\rvert}{(R)^{2}}=10N\)
1. La distance intervient au carré (\(R^{2}\)): si la distance double, on se retrouve avec un facteur \((2R)^{2}=4R^{2}\) au dénominateur. La force est divisée par un facteur 4 et vaut 2,5N
\(\\\)
2. Le produit \(\lvert q_{1}.q_{2}\rvert\) devient \(\lvert 2q_{1}.q_{2}\rvert\). La force est simplement doublée et vaut 20N.
\(\\\)
3. Le produit \(\lvert q_{1}.q_{2}\rvert\) devient \(\lvert 2q_{1}.2q_{2}\rvert\). La force est quadruplée, elle vaut 40N.
\(\\\)
4. On se retrouve avec un facteur \((\frac{R}{3})^{2}=\frac{R^{2}}{9}\) au dénominateur. On a:
\(\\\)
\(F=9.10^{9}.\frac{\lvert q_{1}.q_{2}\rvert}{\frac{R^{2}}{9}} = 9.10^{9}.\lvert q_{1}.q_{2}\rvert\) \(.\frac{9}{R^{2}}=90N\)
Exercice II: Force électrique résultante de deux charges sur une troisième
Dans cet exercice, il y a 3 charges électriques et on détermine la force résultante exercée par deux d’entre elles sur la 3ème.
Enoncé Ex.2 (Source: EXMD 2020)
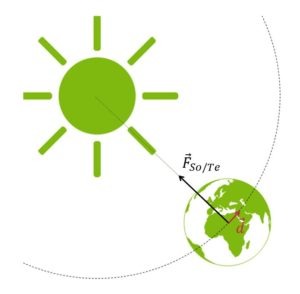
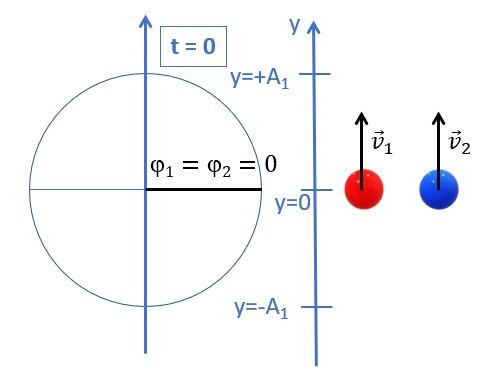
Sur la figure ci-dessous, on suppose que les deux charges électriques ponctuelles Q situées aux points se trouvant sur l’axe y sont positives. Si on place une charge ponctuelle négative -Q au point P, comment sera orientée la force électrique résultante agissant sur cette dernière?
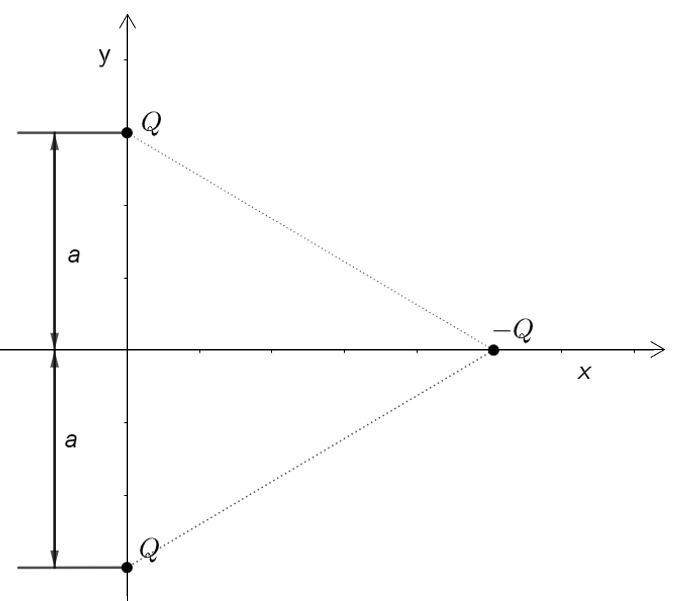
- Vers la gauche, le long de l’axe x
- Vers la droite, le long de l’axe x
- Verticalement vers le bas
- Verticalement vers le haut
Solution Ex.2
Ici, le mot « résultante » est important. Il nous rappelle (au cas où on l’aurait oublié) qu’il y a, à proximité de la charge \(-Q\), deux autres charges: il y a donc deux vecteurs force à prendre en compte. D’après les solutions proposées, on remarque qu’il n’est pas nécessaire de faire des calculs numériques; d’ailleurs, on ne nous donne aucune valeur. Pourtant, puisqu’on doit additionner des vecteurs, leurs intensités ont de l’importance, mais il suffit de les comparer les unes aux autres.
On remarque qu’entre chacune des deux charges \(Q\) (situées sur l’axe y) et la charge \(-Q\), il y a la même distance. Comme, par ailleurs, les charges sont identiques, la force d’attraction entre la charge \(Q\) située en-haut et la charge \(-Q\), a la même valeur que la force d’attraction entre la charge \(Q\) située en bas et la charge \(-Q\).
Attention: soucre d’erreur: ne pas dessiner les forces au bon endroit. On nous parle de la force résultante SUR LA CHARGE \(-Q\); c’est donc sur elle et uniquement sur elle, qu’il faut dessiner les forces électriques.
Comme les charges s’attirent (elles sont de signes opposés), les deux vecteurs que nous devons dessiner partent de la charge \(-Q\) et vont vers chacune des charges \(Q\).
\(\\\)
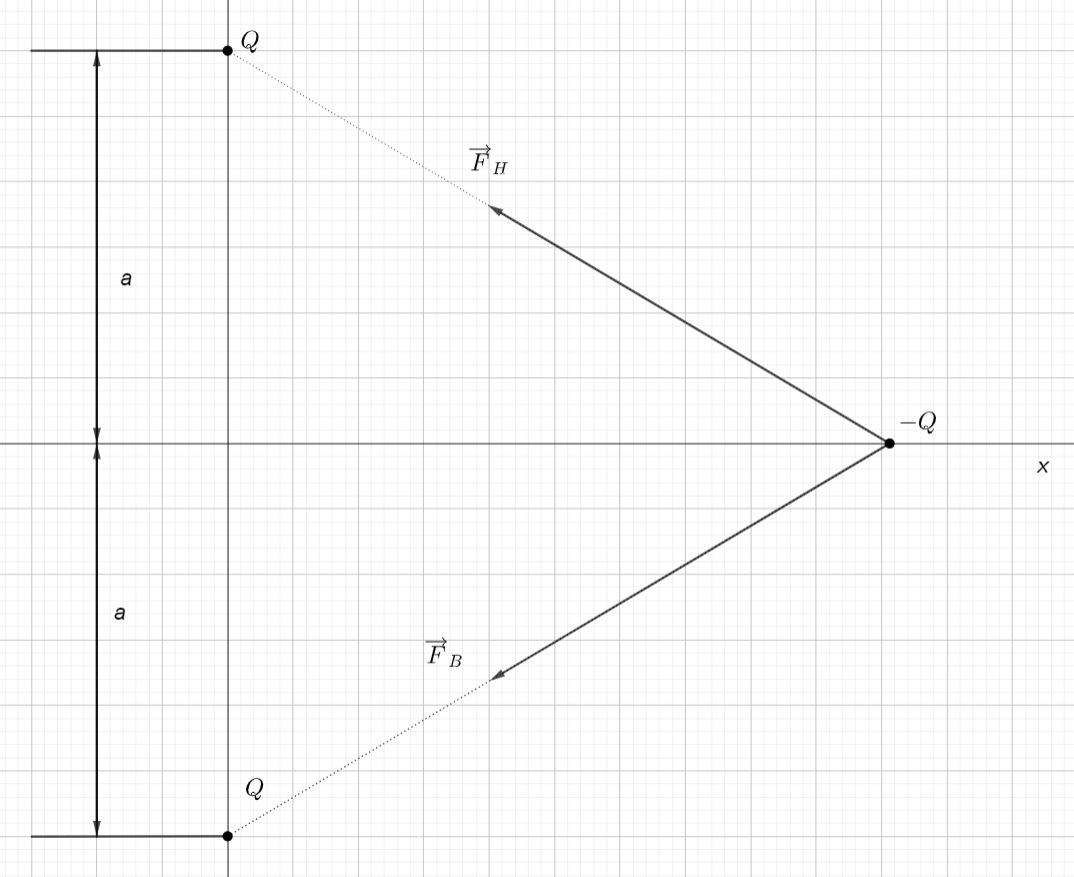
\(\\\)
Pour additionner les forces (puisqu’elles n’agissent pas dans les mêmes directions), il faut les décomposer:
\(\\\)
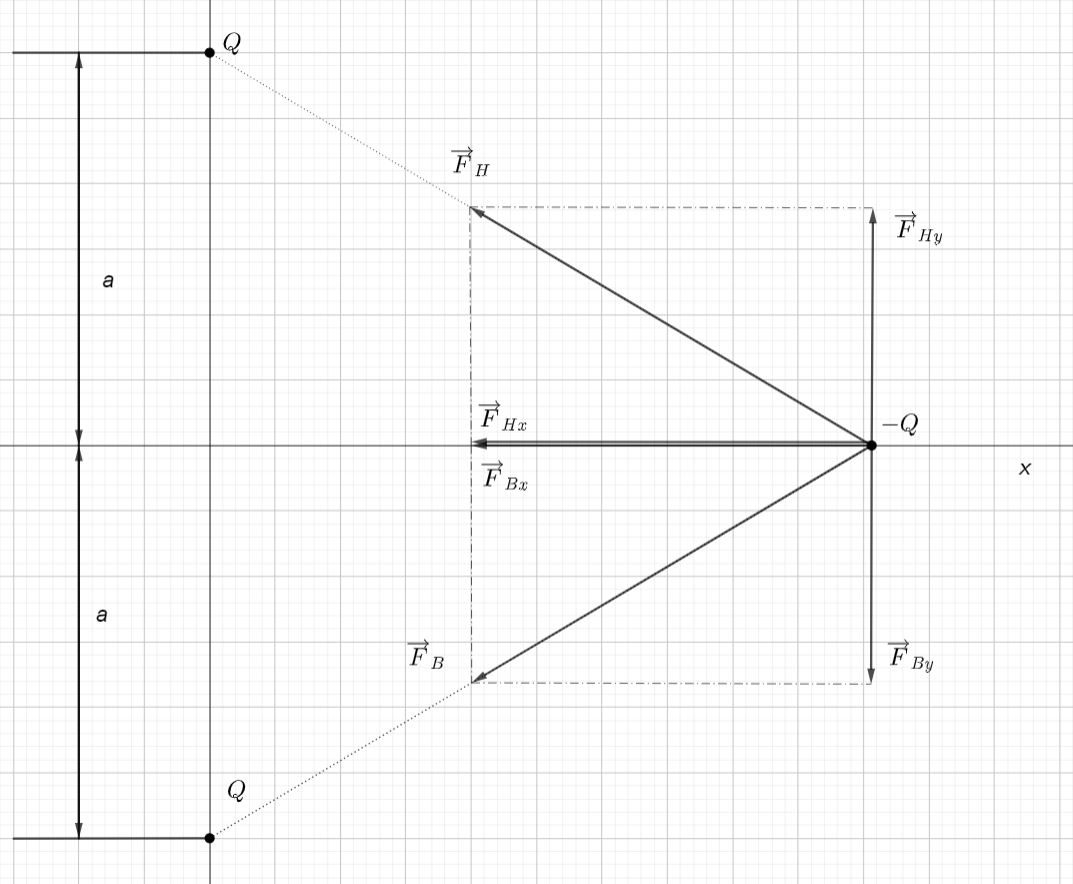
\(\\\)
Les composantes verticales \(\vec{F}_{Hy}\) et \(\vec{F}_{By}\) ont bien entendu la même valeur et sont de sens opposé, elles s’annulent.
Il reste les deux composantes horizontales, \(\vec{F}_{Hx}\) et \(\vec{F}_{Bx}\), identiques et dans le mêmes sens qui vont donner lieu à une force horizontale deux fois plus grande vers la gauche. La bonne réponse est donc « 1.Vers la gauche, le long de l’axe x ».
Remarquons que tout le raisonnement est nécessaire puisque, si une des deux forces était plus grande que l’autre, la force résultante ne serait pas horizontale mais oblique.
Exercice III: Force électrique résultante de trois charges sur une quatrième
Si tu as bien pigé l’exercice II, celui-ci ne devrait te poser aucun problème!
Enoncé Ex.3 (Source: EXMD 2020)
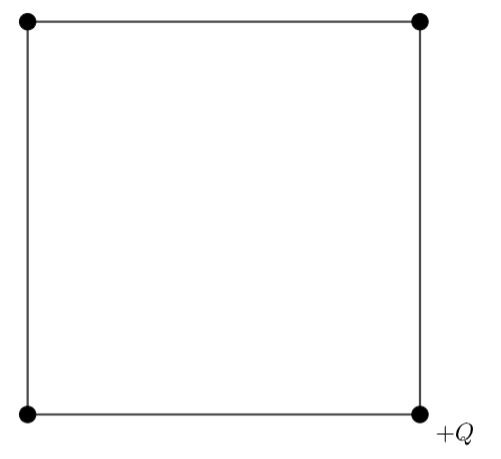
Trois charges électriques identiques sont disposées sur les coins d’un carré comme le représente le dessin suivant. On place une charge électrique positive dans le quatrième coin.
\(\\\)
 \(\\\)
\(\\\)
Quelle est la direction de la force résultante qui s’exerce sur cette charge?
A. Vers la droite.
B. Vers le bas.
C. Vers l’intérieur du carré.
D. Suivant la diagonale du carré.
C’est similaire à l’exercice précédent, à ceci près qu’on ne donne pas le signe des 3 charges déjà présentes. A toi de voir si cela change quelque chose ou pas…
\(\\\)
\(\\\)
…
\(\\\)
\(\\\)
…
\(\\\)
On corrige ensemble?
Solution Ex.3
Si on envisage les deux cas de figure: soit les 3 charges sont positives et les forces électriques avec \(+Q\) sont répulsives, c’est le schéma de gauche. Soit les 3 charges sont négatives et les forces sont alors attractives, c’est le schéma de droite. On se souvient qu’on étudie la charge déposée sur le sommet inférieur droit; on ne dessine les forces que sur cette charge.
\(\\\)
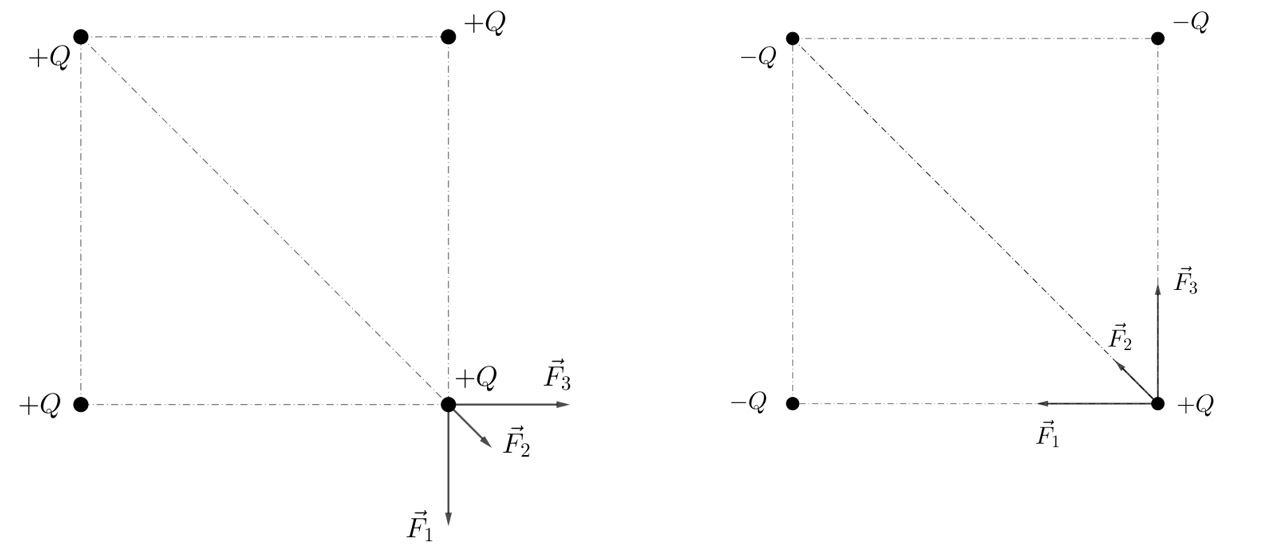
\(\\\)
La distance entre la charge \(+Q\) d’intérêt et la charge parfaitement au-dessus d’elle est la même que la distance entre la charge d’intérêt et celle parfaitement à sa gauche, puisque les charges sont sur les sommets d’un carré. Les forces numérotées \(\vec{F}_{1}\) et \(\vec{F}_{3}\) ont donc la même intensité. Par contre, la charge située au bout de la diagonale est à une distance \(\sqrt{2}\) fois plus grande (en effet, si le côté du carré est noté \(a\), la diagonale vaut \(\sqrt{2}a\)) et la force \(\vec{F}_{2}\) sera donc 2 fois plus petite que les deux autres (rappelle-toi que la distance intervient au carré! Si tu as oublié, vas relire l’exercice I).
Il faut additionner les vecteurs \(\vec{F}_{1}\), \(\vec{F}_{2}\) et \(\vec{F}_{3}\). Il est évident que la somme de \(\vec{F}_{1}\) et \(\vec{F}_{3}\) est orientée le long de la diagonale. Le vecteur \(\vec{F}_{3}\) s’ajoutera ensuite simplement à \(\vec{F}_{1}+\vec{F}_{2}\). La réponse est donc la D! Dans le 1er cas, la résultante sera le long de la diagonale et sortante, dans le second, elle sera le long de la diagonale et rentrante!
Exercice IV: Calcul d’une force électrique résultante en direction ET en intensité
La dernière difficulté consiste à combiner les 3 exercices qui précèdent, en ce sens qu’il faut trouver l’orientation d’une force résultante et sa valeur.
Enoncé Ex.4 (Source: EXMD 2020)
Trois charges électriques ponctuelles sont disposées comme sur le schéma ci-dessous:
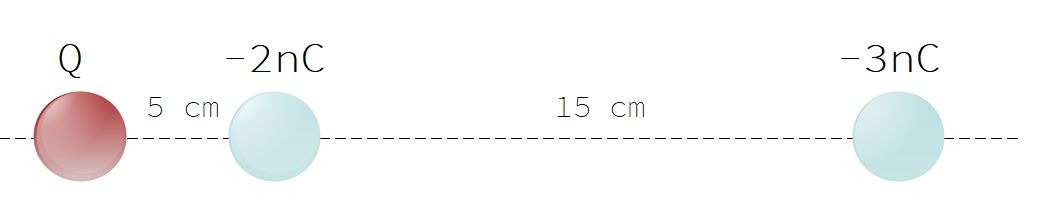
\(\\\)
Que doit valoir la charge \(Q\) pour que la force résultante s’exerçant sur la charge de \(-2nC\) soit nulle? (le symbole nC signifie nanoCoulomb)
A. -1/3 nC
B. -1 nC
C. -2 nC
D. -3 nC
\(\\\)
Je ne sais pas si tu as remarqué, mais on combine ici tout l’article: le fameux nano qui te dit \(10^{-9}\), la valeur des charges et leurs distances respectives qui vont te permettre d’utiliser la loi de Coulomb pour calculer les intensités des forces électriques, et enfin, le fameux terme « résultante » qui te rappelle que tu te prépares à additionner plusieurs forces!
S’ajoute une nouveauté: il faut que la résultante SUR LA CHARGE DE -2nC soit nulle. On se concentre donc, exclusivement sur la charge centrale pour dessiner les vecteurs force! Tu sais que cette charge est soumise à deux vecteurs force (la force qui vient de la 1ère charge et celle de la 3ème). Si tu veux une résultante nulle, il te faut une force vers la gauche et une force vers la droite!
\(\\\)
C’est bon, j’ai assez bossé, là, c’est à ton tour…
\(\\\)
…
\(\\\)
Solution Ex.4
Alors, bon, c’est pas mal d’avoir vu tout ce qui précède, mais avant de te lancer tête baissée dans l’application de la loi de Coulomb, observe que les distances respectives de \(5cm\) et de \(15cm\); ben, Y’a un facteur 3 qui les sépare! Du coup, pas besoin de se casser la tête! On veut deux choses:
- Que les forces aient la même valeur (peu importe laquelle!!)
- Que les forces soient de sens opposés
Si tu te souviens du premier énoncé, si la distance est divisée par \(3\), la force est divisée par \(9\)! Donc pour obtenir deux forces de même intensité, il faudrait que la charge \(q_{1}\) soit 9 fois plus petite que la charge \(q_{3}\) puisqu’elle est 3 fois plus proche de la charge \(q_{2}\) (et que la distance intervient au carré; t’as pas oublié!)! On a donc:
\(\lvert q_{1}\rvert =\frac{\lvert q_{3}\rvert }{9}=\frac{\lvert -3nC\rvert }{9}=\frac{1}{3}nC\)
Il ne reste plus qu’à trouver le signe de la charge (même si, franchement, ils nous aident, là, sur ce coup-là, avec leurs propositions… mais bon, ça permet de se rassurer):
Puisque les charges \(q_{2}\) et \(q_{3}\) se repoussent, \(q_{3}\) exerce sur \(q_{2}\), une force vers la gauche. Il faut donc que \(q_{1}\) exerce sur \(q_{2}\) une force vers la droite. En d’autres termes, il faut que \(q_{1}\) pousse \(q_{2}\) plus loin. On veut une répulsion, il faut le même signe que \(q_{2}\) et \(q_{1}\) est bien négative! TADAMMMM!!!
C’est bien la réponse A.
\(q_{1}=-\frac{1}{3}nC\)
\(\\\)
Rmq: Si tu ne penses pas à réfléchir ainsi et que tu appliques la loi de Coulomb pour trouver la valeur de la première force, tu vas trouver ceci:
\(F=9.10^{9}.\frac{\lvert -2.10^{-9}.-3.10^{-9}\rvert}{0,15^{2}} = ???\) GLOOPS
Rappelle-toi que tu n’as pas de calculatrice et que c’est pas super sympa ce calcul…. signe qu’il y a plus simple! Ceci dit, tu peux toujours t’en sortir en remarquant que \(0,15=\frac{3}{20}\). Tu aurais:
\(F=9.10^{9}.\frac{\lvert -2.10^{-9}.-3.10^{-9}\rvert}{(\frac{9}{400})} = \frac{6.10^{-9}}{\frac{1}{400}}=2,4.10^{-6}N \)
Mais, c’est quand même vachement plus compliqué, parce qu’après, tu dois exprimer que la force entre \(q_{1}\) et \(q_{2}\) doit avoir la même valeur. Tu as:
\(2,4.10^{-6}=9.10^{9}.\frac{\lvert -Q.-2.10^{-9}\rvert}{(5.10^{-2})^{2}} = \frac{Q.18}{25.10^{-4}}\)
\(\\\)
\(\Leftrightarrow Q=\frac{25.10^{-4}.2,4.10^{-6}}{18}=\frac{60.10^{-10}}{18}=\frac{6.10^{-9}}{18}=\frac{1}{3}nC\)\(\\\)
\(\\\)
OUFTI!!!! Je te conseille quand même de scruter les énoncés et de voir si les distances considérées sont multiples l’une de l’autre!!!
\(\\\)
\(\\\)
Ceci clôture cet article. En ce qui concerne l’examen d’entrée en Médecine/dentisterie (je propose des ressources YT ici), il n’y a pas eu plus compliqué ces deux dernières années. Par contre, si tu veux vraiment te préparer à vivre un bac scientifique, c’est bien de relever encore un tantinet le niveau. Si tu es motivé(e), je te propose au bas de cette page, un cahier d’exercices progressifs avec solutions pour la modique somme de 27€! Et comme tu peux toujours me poser tes questions, je parie que tu ne trouveras pas moins cher ailleurs!
\(\\\)
Si tu en as ta dose, très bien, mais si je t’ai aidée, donne moi un like ici tout en bas de la page! Ben quoi, tout travail mérite salaire, non?
\(\\\)
Allez, bonne chance et bon courage pour la suite! Si tu préfères les supports vidéos, la théorie et la comparaison entre la force électrique et la force gravifique (le poids, quoi!) sont repris ici!
\(\\\)
Le cahier est structuré de la façon suivante:
- Rappel des formules et valeurs importantes
- Six exercices-type résolus en détail, suivis d’un ou plusieurs exercices pour s’entraîner
- Les solutions détaillées des exercices supplémentaires

Pour te procurer ce cahier, clique sur le bouton « Acheter » de Paypal ci-dessous!





 \(\\\)
\(\\\)