Recevez gratuitement
mon livret!
Cet article présente le déroulement d’un exercice dans lequel on utilise le principe fondamental de la dynamique (noté par la suite PFD) pour déduire la valeur de l’accélération de deux blocs glissant sur des plans inclinés et reliés entre eux par des cordes tendues comme le montre la figure suivante. La corde est toujours considérée comme étant de masse négligeable, si bien que la tension y est partout la même.
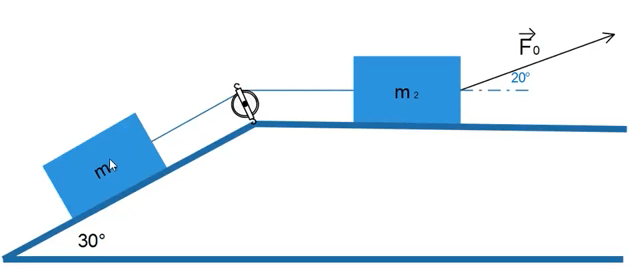
L’énoncé à résoudre est le suivant: Quelle intensité de force \(F_{0}\) faut-il exercer pour que les blocs se déplacent vers la droite avec une accélération de 2 m/s²? Le premier bloc a une masse \(m_{1}=3kg\) et le second \(m_{2}=5kg\). Le coefficient de frottement cinétique entre le bloc et le plan est \(\mu_{c}=0,25\).
Il faut tout d’abord se souvenir qu’une poulie fixe a pour seul effet la modification de la direction des forces appliquées. Cet exercice correspond donc simplement à un mouvement accéléré sur la paroi.
1. Identification des forces en présence
Dans cet exercice, il s’agit d’étudier le mouvement des deux masses \(m_{1}\) et \(m_{2}\). Il nous faut donc tout d’abord identifier les forces en présence. Pour ce faire, travailler de façon méthodique est très efficace. Il y a une série de questions à se poser. Commençons avec l’étude de la 1ère masse.
1.1.Etude de \(m_{1}\)
- Que vaut la force poids? L’exercice se déroule à la surface de la Terre, on peut donc écrire: \(F_{G_{1}} \ = \ m_{1}.g \ = \ 3.10 \ = \ 30[N] \). On peut dessiner le vecteur \(\overrightarrow{F}_{G1}\) verticalement vers le bas
- Qui d’autre agit sur la masse à distance? Personne puisqu’il n’est pas question d’influences électriques ou magnétiques.
- Qui touche le bloc? Si on regarde la première masse, on s’aperçoit qu’elle est touchée par la surface sur laquelle elle prend appui et par la corde tendue. Elle subit donc plusieurs forces.
- Le bloc prend appui sur la paroi (on pourrait noter cette force \(\overrightarrow{F}_{bloc 1/paroi}\), mais cette force ne nous intéresse pas vraiment étant donné qu’elle agit sur la paroi et pas sur la masse 1). Toutefois, étant donné que le bloc prend appui sur la paroi, cette dernière réagit (selon le principe des actions réciproques) et il existe donc une force dite de réaction normale, notée \(\overrightarrow{N}_{1}\) qui est une force exercée par la paroi sur le bloc 1. Comme son nom (‘normal’) l’indique, cette force agit perpendiculairement à la surface d’appui.
- L’énoncé nous apprend que le bloc glisse vers la droite. Il y a donc une force de frottement cinétique. Pour trouver son sens, il suffit de se placer sur le bloc et de regarder dans quel sens ‘file’ la paroi: elle semble glisser vers la gauche; la force de frottement cinétique agit donc parallèlement vers la gauche. On la note \(\overrightarrow{F}_{f_{c1}}\). (Rappel)
- Enfin, la corde exerce une force de traction sur le bloc qui agit dans la direction de la corde. On la note: \(\overrightarrow{T}\).
Remarquez qu’il n’y a pas d’indice 1 sur la force de tension. C’est normal car cette force est identique dans toute la corde. On retrouvera donc exactement la même force sur le bloc 2. Dès lors, mettre des indices 1 et 2 nous amènerait à croire qu’il y a deux inconnues alors qu’il n’y en a qu’une: si on connait la tension sur \(m_{1}\), on connait d’office la tension sur \(m_{2}\).
On peut donc représenter ces forces comme sur la Fig.2.
1.2.Etude de \(m_{2}\)
- Que vaut la force poids? L’exercice se déroule à la surface de la Terre, on peut donc écrire: \(F_{G_{2}} \ = \ m_{2}.g \ = \ 5.10 \ = \ 50[N] \). On peut dessiner le vecteur \(\overrightarrow{F}_{G_{2}}\) verticalement vers le bas
- Qui d’autre agit sur la masse à distance? Personne puisqu’il n’est pas question d’influences électriques ou magnétiques.
- Qui touche le bloc? Si on regarde la seconde masse, on s’aperçoit qu’elle est touchée par la surface sur laquelle elle prend appui, par la corde tendue et par un troisième acteur qui exerce la force notée \(F_{0}\). Elle subit donc plusieurs forces.
- Le bloc prend appui sur la paroi, cette dernière réagit (selon le principe des actions réciproques) et il existe donc une force dite de réaction normale, notée \(\overrightarrow{N}_{2}\) qui agit perpendiculairement à la surface d’appui.
- L’énoncé nous apprend que le bloc glisse vers la droite. Il y a donc une force de frottement cinétique qui agit parallèlement à la paroi et vers la gauche. On la note \(\overrightarrow{F}_{f_{c2}}\).
- La corde exerce une force de traction sur le bloc qui agit dans la direction de la corde. On la note: \( \overrightarrow{T} \).
- Enfin, il y a l’action de la force motrice \( \overrightarrow{F}_{0}\) qui est déjà représentée sur la figure, ce qui nous conduit à la représentation de la Fig.3.
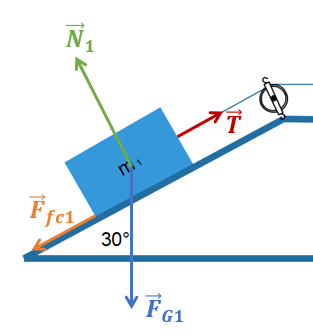
On peut donc représenter ces forces comme sur la Fig.3.
\( \\ \)
2. Etude du mouvement des blocs
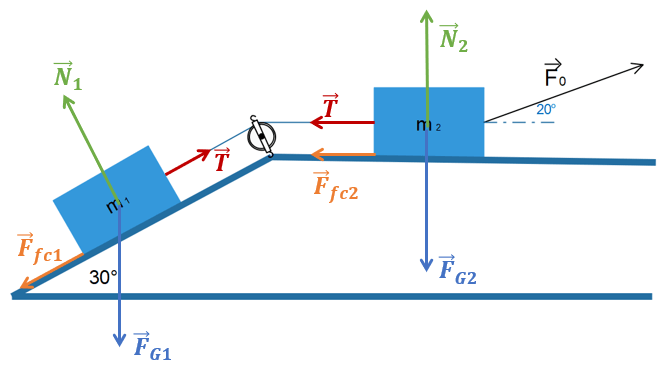
Nous savons, d’après l’énoncé, que le bloc glisse le long de la paroi. Il effectue donc un mouvement rectiligne uniformément accéléré (si on oublie la poulie qui a comme seul rôle de modifier les directions des forces de tension dans la corde). En toute logique, nous prendrons donc le plan comme direction X et le sens du mouvement comme sens de ce référentiel.
Afin de pouvoir utiliser la trigonométrie, il faut également tracer l’axe Y du référentiel, et décomposer toutes les forces qui ne sont pas strictement orientées selon X ou Y. Il s’agit des forces \(\overrightarrow{F}_{G1} et \overrightarrow{F}_{0}\). Nous obtenons la Fig.4.
\( \\ \)
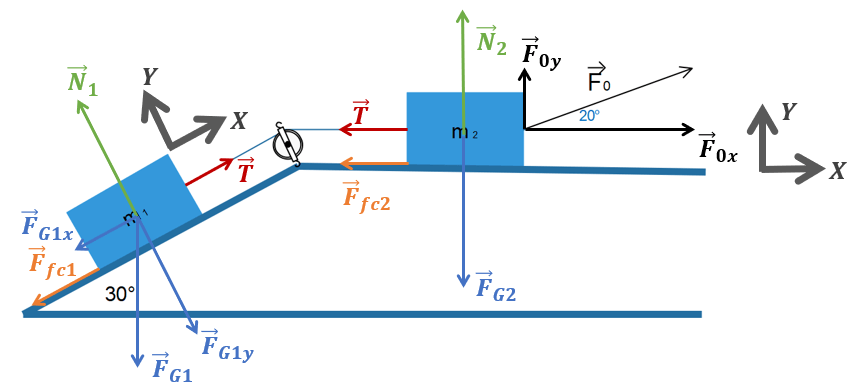
Une bonne méthode, est de systématiquement exprimer les composantes de forces à l’aide de la trigonométrie. Nous obtenons:
\[F_{0x} \ = \ F_{0}.cos(20) \tag{1} \]
\[F_{0y} \ = \ F_{0}.sin(20) \tag{2} \]
\[F_{G1x} \ = \ F_{G1}.sin(30) = \ 30.sin(30) \ = \ 15[N] \tag{3} \]
\[F_{G1y} \ = \ F_{G1}.cos(30) = \ 30.cos(30) \ = \ 26[N] \tag{4} \]
\( \\ \)
Nous ne savons rien de la force de tension mais nous savons que la force de frottement cinétique est de la forme suivante: \(F_{fc} \ = \ \mu_{c}.N \). Nous pouvons donc écrire:
\( \\ \)
\[F_{fc1} \ = \ \mu_{c}.N_{1} = \ 0,25.N_{1} \tag{5} \]
\[F_{fc2} \ = \ \mu_{c}.N_{2} = \ 0,25.N_{2} \tag{6} \]
2.1.Etude du mouvement de \(m_{1}\)
a. Le long de l’axe X
On souhaite une accélération parallèle au plan et vers la droite, le vecteur accélération aura donc une composante scalaire positive dans le référentiel X choisi. Appliquons le principe fondamental de la dynamique. Que dit-il?
En mathématique:
\[\Sigma \overrightarrow{F}_{x} \ = \ m.\overrightarrow{a}_{x} \tag{7} \]
En français:
Si une force résultante agit sur une masse, elle lui communique une accélération parallèle et de même sens, dont l’intensité est donnée par la relation scalaire \(\Sigma F_{x} \ = \ m.a_{x}\). Il nous faut donc observer les composantes de forces le long du référentiel X et exprimer le PFD pour le bloc 1.
\( \\ \)
En partant de la gauche, le long du plan incliné, càd de X, nous rencontrons:
- la force \( \overrightarrow{F}_{fc1}\) qui est opposée au référentiel X et qui possède donc une composante scalaire négative: \(-F_{fc1}\)
- la force \( \overrightarrow{F}_{G1x}\) qui est opposée au référentiel X et qui possède donc une composante scalaire négative: \(-F_{G1x}\)
- la force \( \overrightarrow{T}\) qui est dans le sens du référentiel X et qui possède donc une composante scalaire positive: \(T\)
Nous pouvons donc écrire le PFD, respectivement d’après les relations 7, 3 et 5:
\begin{align}
– F_{fc1} \ – F_{G1x} \ + \ T &= m_1.a \\
– \mu_{c}.N_{1} \ – 15 \ + \ T &= 3.2 \\
– 0,25.N_{1} \ + \ T &= 21 \tag{8} \\
\end{align}
b. Le long de l’axe Y
Il n’y a aucun mouvement de la masse le long de l’axe Y puisqu’elle se contente de glisser le long de l’axe X. Nous pouvons dès lors écrire:
\[\Sigma \overrightarrow{F}_{y} \ = \ m.\overrightarrow{a}_{y} \ = \ \overrightarrow{0} \]
ou encore
\[\Sigma F_{y} \ = \ m.a_{y} \ = \ 0 \tag{9} \]
Il nous faut donc observer les composantes de forces le long du référentiel Y et exprimer le PFD pour le bloc 1.
\( \\ \)
En partant du bas, le long de l’axe Y, nous rencontrons:
- la force \( \overrightarrow{F}_{G1y}\) qui est opposée au référentiel Y et qui possède donc une composante scalaire négative: \(-F_{G1y}\)
- la force \( \overrightarrow{N}_{1}\) qui est dans le sens du référentiel Y et qui possède donc une composante scalaire positive: \(+ N_{1}\)
Nous pouvons donc écrire le PFD (9):
\begin{align}
– F_{G1y} \ + N_{1} &= 0 \\
– 26 + N_{1} &= 0 \\
N_{1} &= 26 \\
\end{align}
Ce qui nous permet de réécrire la relation (8):
\begin{align}
– 0,25.26 \ + T &= 21 \\
– 6,5 + T &= 21 \\
T &= 27,6 \tag{10} \\
\end{align}
2.2.Etude du mouvement de \(m_{2}\)
a. Le long de l’axe X
Comme pour \(m_{1}\), appliquons le principe fondamental de la dynamique à \(m_{2}\).
\( \\ \)
En partant de la gauche, le long du plan incliné, càd de X, nous rencontrons:
- la force \( \overrightarrow{F}_{fc2}\) qui est opposée au référentiel X et qui possède donc une composante scalaire négative: \(-F_{fc2}\)
- la force \( T\) qui est opposée au référentiel X et qui possède donc une composante scalaire négative: \(-T\)
- la force \( \overrightarrow{F}_{0x}\) qui est dans le sens du référentiel X et qui possède donc une composante scalaire positive: \(+\overrightarrow{F}_{0x}\)
Nous pouvons donc écrire le PFD:
\begin{align}
– F_{fc2} \ – \ T \ + F_{0x} &= m_2.a \\
– \mu_{c}.N_{2} \ – 27,6 \ + \ F_{0}.cos(20) &= 5.2 \\
– 0,25.N_{2} \ + \ F_{0}.cos(20) &= 37,6 \tag{11} \\
\end{align}
b. Le long de l’axe Y
Il n’y a aucun mouvement de la masse le long de l’axe Y puisqu’elle se contente de glisser le long de l’axe X. Nous pouvons dès lors écrire:
\[\Sigma F_{y} \ = \ m.a_{y} \ = \ 0 \]
Il nous faut donc observer les composantes de forces le long du référentiel Y et exprimer le PFD pour le bloc 2.
\( \\ \)
En partant du bas, le long de l’axe Y, nous rencontrons:
- la force \( \overrightarrow{F}_{G2}\) qui est opposée au référentiel Y et qui possède donc une composante scalaire négative: \(-F_{G2}\)
- la force \( \overrightarrow{N}_{2}\) qui est dans le sens du référentiel Y et qui possède donc une composante scalaire positive: \(+ N_{2}\)
- la force \( \overrightarrow{F}_{0y}\) qui est dans le sens du référentiel Y et qui possède donc une composante scalaire positive: \(+ F_{0y}\)
Nous pouvons donc écrire le PFD:
\begin{align}
– F_{G2} \ + N_{2} \ + \ F_{oy} &= 0 \\
– 50 + N_{2} \ + \ F_{0}.sin(20) &= 0 \\
N_{2} &= 50 \ – \ F_{0}.sin(20) \tag{12} \\
\end{align}
Ce qui nous permet de réécrire la relation (11):
\begin{align}
– 0,25. \Bigg(50 \ – \ F_{0}.sin(20) \Bigg) \ + \ F_{0}.cos(20) &= 37,6 \\
– 0,25.50 \ + \ 0,25.F_{0}.sin(20) \ + \ F_{0}.cos(20) &= 37,6 \\
0,25.F_{0}.sin(20) \ + \ F_{0}.cos(20) &= 50,1 \\
F_{0} \Bigg(0,25.sin(20) \ + \ cos(20) \Bigg) &= 50,1 \\
F_{0} &= \frac{50,1}{0,25.sin(20) \ + \ cos(20) } \\
F_{0} &= 48,9 \\
\end{align}
Conclusion
La force à exercer pour que le système possède une accélération de 2 m/s² vers la droite est une force de 49 N orientée vers la droite, à 20° au-dessus de l’horizontale!
Rmq: Attention, dans la version vidéo de cet exercice, il y a une erreur de calcul en fin de développement, navrée…
Lien vers l’exercice résolu en vidéo
\(\\\) P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile. Merci!
Partager l'article:
administrator
2 commentaires pour l’instant
François-Yves ClaveauPublié le12:16 am - Mai 7, 2020
Merci beaucoup pour la qualité pédagogique de ce document .
À propos de l’auteur