Ce que tu dois savoir pour trouver le déplacement d’un MRUA en moins d’une minute:
Tu te rappelles de l’aire d’un triangle?
\(Aire=\frac{Base\ \bullet \ Hauteur}{2}\)
Alors, tu sais le plus difficile pour calculer le déplacement!
On peut HYPER facilement (en moins d’une minute) déterminer le déplacement dans un MRUA
La raison est simple! Si tu traces le graphique de la vitesse en fonction du temps (simplement l’allure, pas besoin d’être hyper précis!), l’intégrale de cette fonction (ou pour faire plus simple, l’aire sous la courbe), représente le déplacement \(\Delta x\)
Pas de long discours d’explication du comment du pourquoi ici, ça, c’est fait dans la vidéo dont je parle en fin d’article! Là, je vais juste te montrer l’application de ce truc dans 4 exercices repris dans des questions de l’EXMD (Examen d’entrée en Médecine/Dentisterie, en Belgique)! Allons-y, il n’y en a pas pour longtemps!
Exercice 1: tu traces le graphe v(t) pour trouver le déplacement
A l’atterrissage, un avion touche le sol à une vitesse de 180 km/h. Après une décélération uniforme, il s’immobilise 10s plus tard.
Quelle distance au sol parcourt-il avant de s’arrêter?
A. 100m
B. 250m
C. 500m
D. 1000m
Première étape, tu transformes tes unités et tu te fais un mini schéma de la situation, le cerveau est plus efficace sur des images que sur du texte! ça donne, ça:
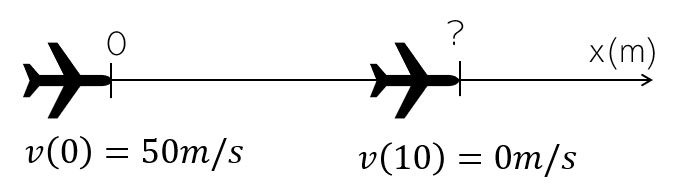
On te parle d’une décélération et d’une distance \(\Rightarrow\) TU DESSINES L’ALLURE DU GRAPHE \(v(t)\) et ça donne ça:
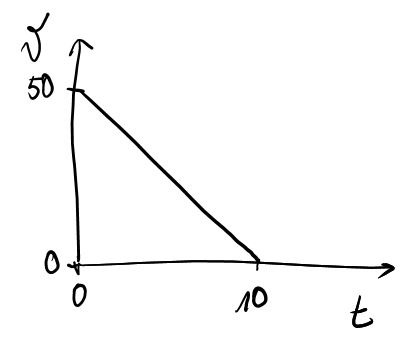
Et tu exprimes que l’aire représente le déplacement! et ça donne ça (puisque tu sais que l’aire d’un triangle, c’est \(\frac{B.H}{2}\)):
\(\\ \)
\(\Delta x = \frac{10.50}{2}=250m\)
\(\\ \)
FINITO! Réponse B
Exercice 2: on te donne déjà le graphe v(t), plus qu’à calculer le déplacement
On considère le mouvement rectiligne d’un mobile. Le graphique ci-dessous représente la vitesse du mobile en fonction du temps sur une durée de 12 secondes.
Quelle est la distance parcourue par le mobile pendant ces 12 secondes?
A. 48m
B. 64m
C. 80m
D. 92m
Alors, là, c’est clair! Le graphique est déjà fait pour toi! Plus qu’à colorier les formes les plus simples et à répondre à la question posée!\(\\ \)
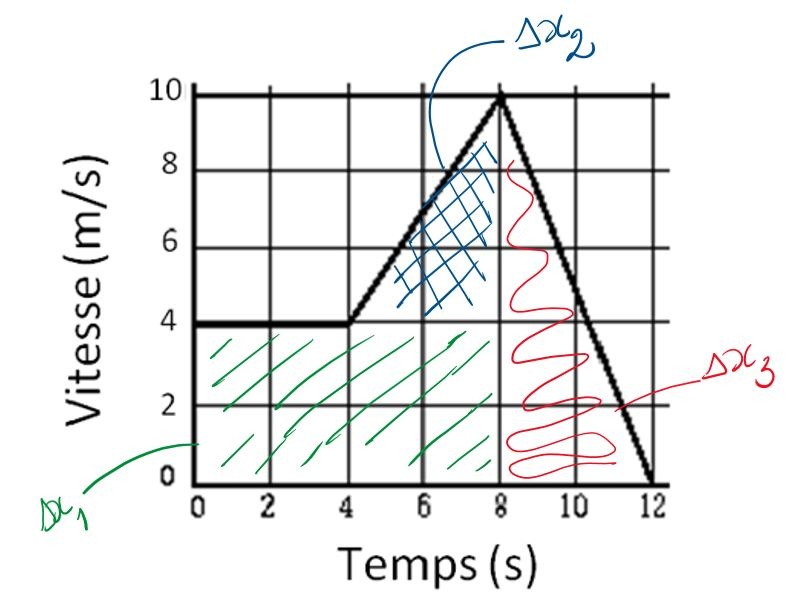
Alors, c’est clair qu’il n’y a pas qu’une réponse possible! On choisit ce qu’on veut comme zones! Pour mon choix, ça donne ça:
\(\Delta x_{1}=4.8=32m\)
\(\\ \)
\(\Delta x_{2}=\frac{4.6}{2}=12m\)
\(\\ \)
\(\Delta x_{3}=\frac{4.10}{2}=20m\)
\(\\ \)
Et donc:
\(\\\)
\(\Delta x=32+12+20=64m\)
\(\\ \)
FINITO! Réponse B
Exercice 3: tu traces encore le graphique v(t) pour trouver le déplacement, même si tu ne connais pas tout!
Une voiture subissant une accélération uniforme passe de 0 à 72 km/h sur une distance de 100m.
En combien de temps a-t-elle atteint cette vitesse?
A. 5s
B. 10s
C. 15s
D. 20s
Alors, là, tu vois qu’on est plus proche du 1er exercice, mais il y a quand même un truc qui cloche, on ne sait pas compléter le graphique avec des valeurs chiffrées, il nous manque le temps!
Ben oui, c’est logique, puisque c’est la question posée!
Dans ce cas, NO STRESS! Comme à chaque fois en physique, quand tu ne sais pas, tu inventes! Non, je plaisante! Quand tu ne sais pas, tu laisses le symbole de la grandeur, ici: \(\Delta t\)!
\(\\ \)
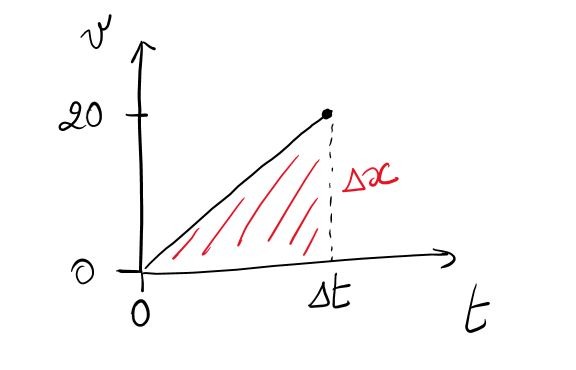
On calcule l’aire rouge:
\(\Delta x=\frac{\Delta t.20}{2}=10.\Delta t\)
\(\\ \)
Or, on sait que le déplacement vaut 100m et donc que \(\Delta x=100m\)
\(\\ \)
Et donc:
\(100=10.\Delta t\)
\(\Leftrightarrow \Delta t = 10s\)
\(\\ \)
Réponse B
Retrouve ces exercices en vidéo (avec quelques explications en plus): Clique ici!
Si tu veux avoir accès à tous les exercices, de tous les genres, sur le MRUA, alors, C’est par ici et par ici!
Bonne continuation dans ton apprentissage de la physique!
