Bienvenue à nouveau sur 'Osez réussir en physique'!
Avez-vous déjà pris le temps de lire mon livret qui vous explique comment reconnaitre et faire parler les outils mathématiques en physique? Si pas, c'est le moment! Cliquez ici pour le télécharger ! 🙂
Avant de commencer à lire ces exercices, as-tu regardé les vidéos suivantes?
MRUA – Etude des graphiques et équations associées
Pourquoi la vitesse et l’accélération peuvent-elles être positives ou négatives?
Exercices résolus en vidéo
Le MRUA: des exercices pour s’entrainer sur les graphiques
Je pars du principe que tu sais utiliser l’outil graphique, parce que, tu es allé lire l’exercice résolu n°1 qui se trouve ici!
Si ce n’est pas le cas, dépêche-toi, il ne faut pas plus de 10 min!
C’est bon? Qu’as-tu retenu? Normalement, que la pente de la tangente au graphique v(t) représente l’accélération instantanée puisque:
\begin{equation}
\ \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta {v}}{\Delta t_{ }}=a
\end{equation}
Mais aussi que l’aire comprise entre la courbe v(t) et l’axe du temps représente la valeur du déplacement \(\Delta x \) puisque:
\begin{equation}
\ v*\Delta t = \Delta x
\end{equation}
Exercices corrigés pas à pas disponibles ici! Fascicule reprenant:
- 3 pages de synthèse sur TOUT ce qu’il faut ABSOLUMENT comprendre avant de se lancer tête baissée dans les exercices sur le MRUA (et de perdre son temps) !
- Les 29 exercices ci-dessous corrigés dans les moindres détails en 41 pages!
Bref, l’équivalent de plus de 10 heures de cours pour moins de 30€ !!!
Clique sur le bouton « Acheter » ci-dessous…

Le MRUA: des exercices à partir du graphique v(t)
\(\\\)
- Soit le graphique horaire de la vitesse d’un objet en MRUV (V signifiant varié, on ne te dit donc pas si c’est accéléré ou décéléré). A l’instant initial, l’objet occupe la position x(0)=0m.
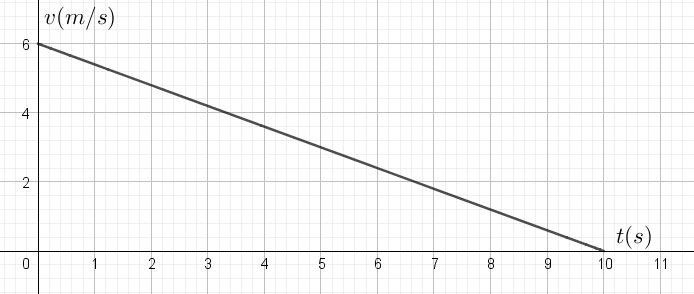
- Le mouvement se fait-il dans le sens du référentiel? Justifie.
- Le mouvement est-il accéléré au sens commun du terme? Justifie.
- Donne l’équation horaire de la vitesse
- Donne l’équation horaire de la position
- Trace l’allure du graphique horaire de la position, x(t), en justifiant.
\(\\\)
- Soit le graphique horaire de la vitesse d’un objet en MRUV. A l’instant initial, l’objet occupe la position x(0)=0m.
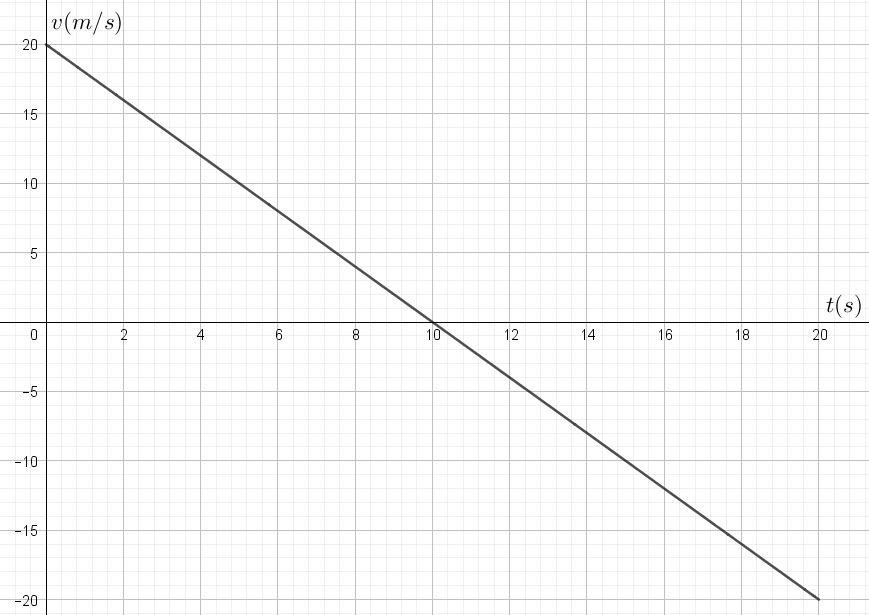
- Le mouvement se fait-il dans le sens du référentiel? Justifie.
- Le mouvement est-il accéléré au sens commun du terme? Justifie.
- Donne l’équation horaire de la vitesse
- Donne l’équation horaire de la position
- Trace l’allure du graphique horaire de la position, x(t), en justifiant.
\(\\\)
- Soit le graphique horaire de la vitesse d’un objet en MRUV. A l’instant initial, l’objet occupe la position x(0)=40m.
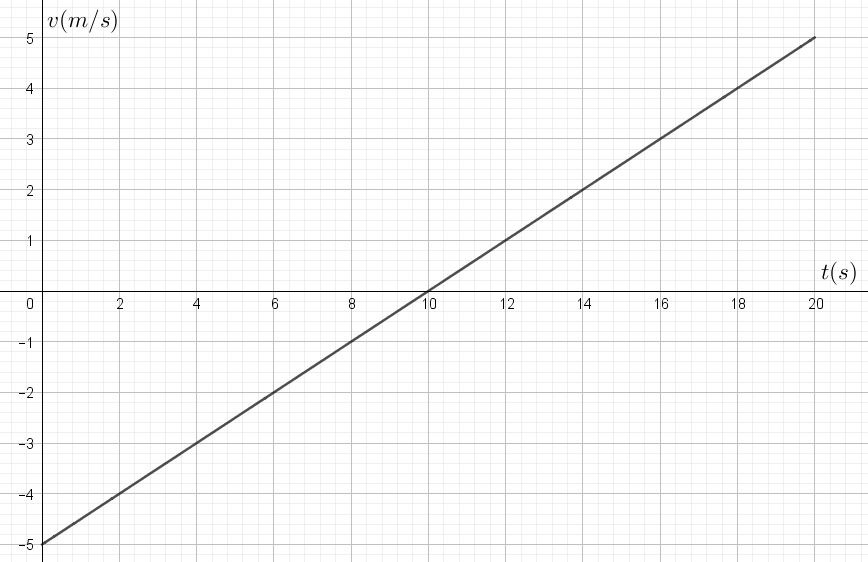
- Le mouvement se fait-il dans le sens du référentiel? Justifie.
- Le mouvement est-il accéléré au sens commun du terme? Justifie.
- Donne l’équation horaire de la vitesse
- Donne l’équation horaire de la position
- Trace l’allure du graphique horaire de la position, x(t), en justifiant.
\(\\\)
- Soit le graphique horaire de la vitesse d’un objet en MRUV. A l’instant initial, l’objet occupe la position x(0)= – 50m.
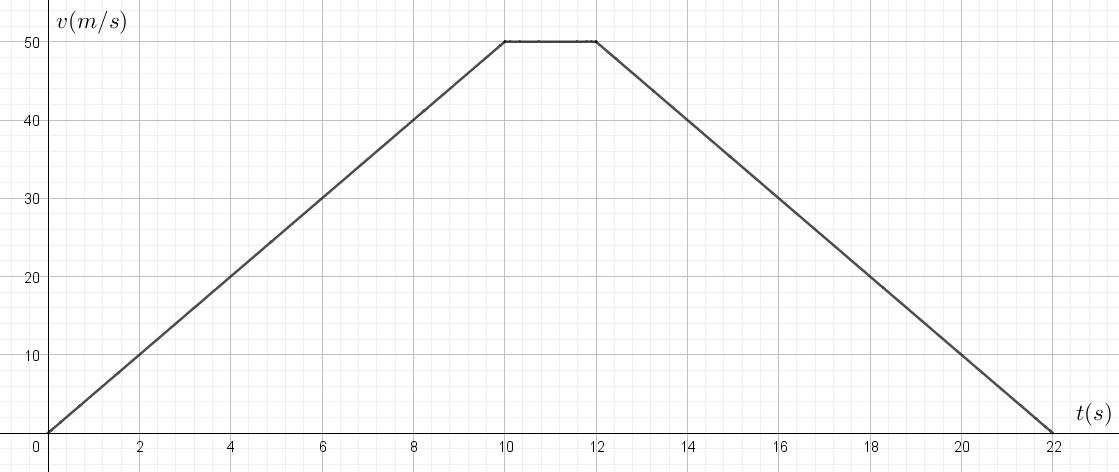
- Le mouvement se fait-il dans le sens du référentiel? Justifie.
- Le mouvement est-il accéléré au sens commun du terme? Justifie.
- Trace l’allure du graphique horaire de la position, x(t), en justifiant.
\(\\\)
- Soit le graphique horaire de la vitesse d’un objet en MRUV. A l’instant initial, l’objet occupe la position x(0)= 200m.
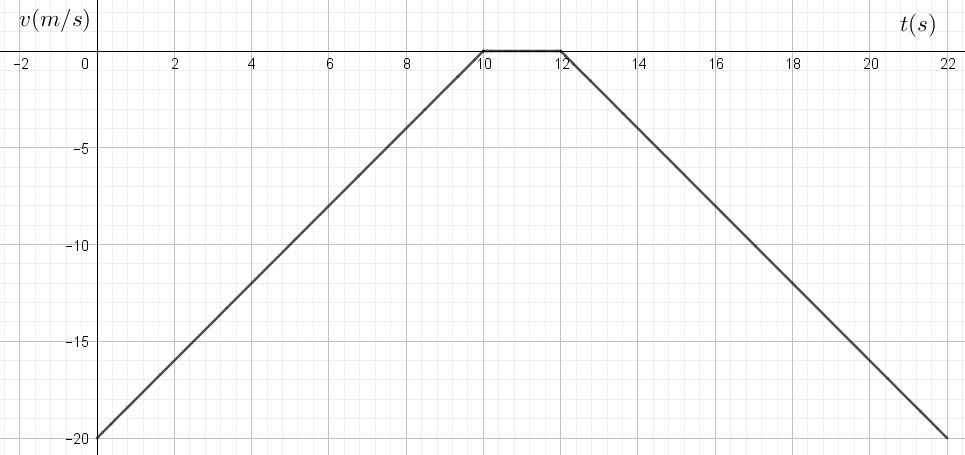
- Le mouvement se fait-il dans le sens du référentiel? Justifie.
- Le mouvement est-il accéléré au sens commun du terme? Justifie.
- Trace l’allure du graphique horaire de la position, x(t), en justifiant.
\(\\\)
- A quel graphe x(t) correspond le graphe v(t) ci-dessous?
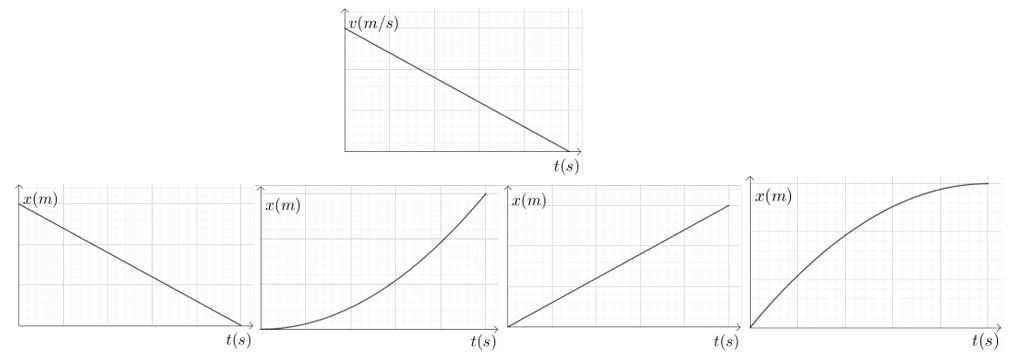
\(\\\)
Le MRUA: des exercices à partir du graphique x(t)
- Pour chacun des 6 graphiques x(t) ci-dessous, donne:
- La position initiale du mobile le long du référentiel X
- Le sens de la vitesse initiale du mobile
- L’évolution de la vitesse initiale (qualitativement) en signe et valeur
- Le sens de l’accélération
\(\\\)
Graphe n°1:
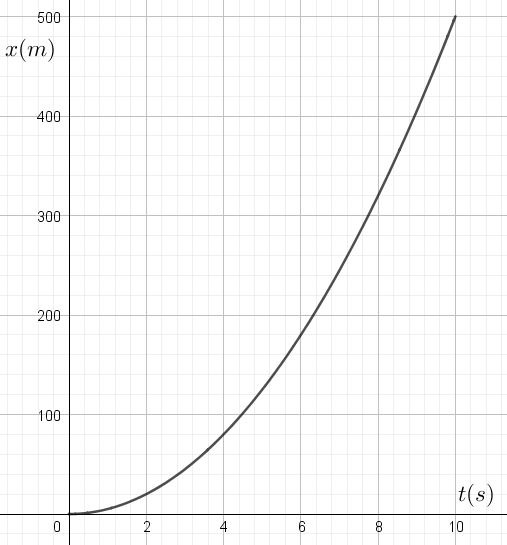
Graphe n°2:
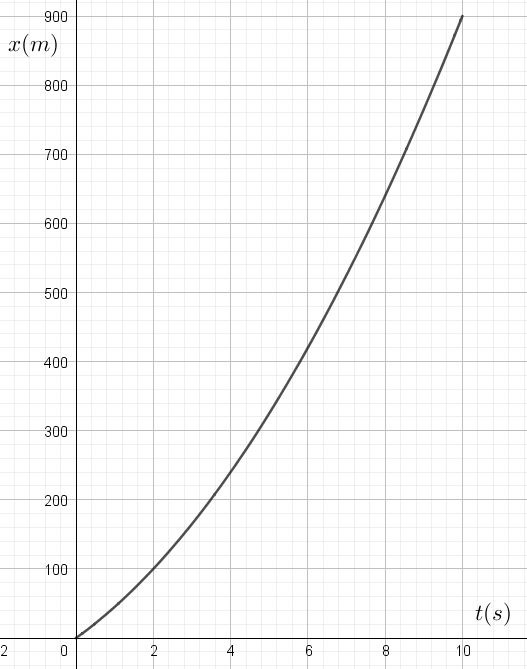
Graphe n°3:
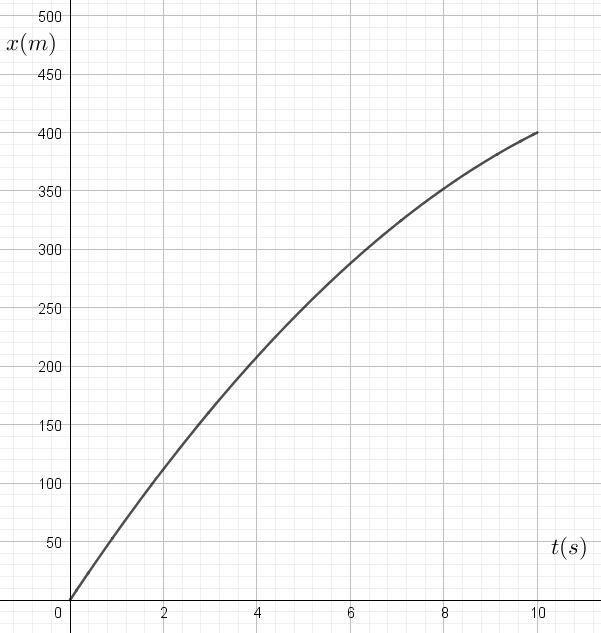
Graphe n°4:
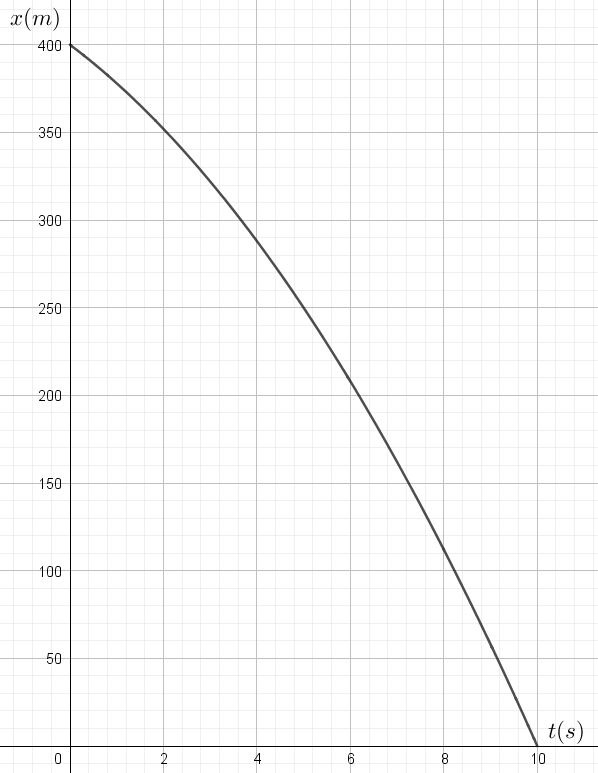
Graphe n°5:
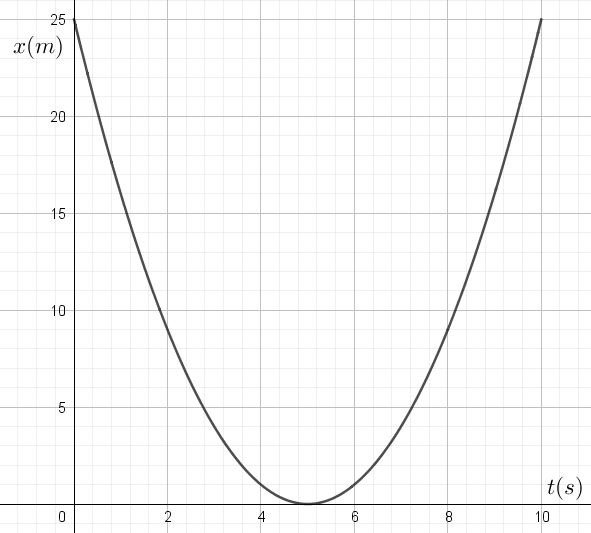
Graphe n°6:
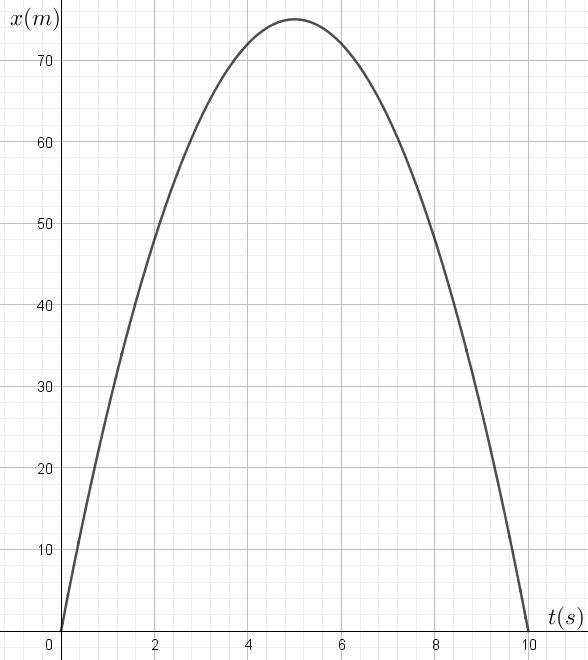
En réalité, les six graphiques que vous venez de caractériser correspondent aux équations suivantes. Est-ce cohérent avec ce que vous venez d’expliquer?
- \(x(t)=5t^2\)
- \(x(t)=40t+5t^2\)
- \(x(t)=60t-2t^2\)
- \(x(t)=400-20t-2t^2\)
- \(x(t)=25-10t+t^2\)
- \(x(t)=30t-3t^2\)
\(\\\)
- Un chariot démarre suivant un MRUA avec une accélération de 2m/s².
- Tracez le graphique donnant sa vitesse pendant les 5 premières secondes du mouvement.
- Calculez les distances parcourues après 2 et 5 secondes.
- Tracez le graphique de l’évolution de la position du chariot pendant les 5 premières secondes du mouvement.
\(\\\)
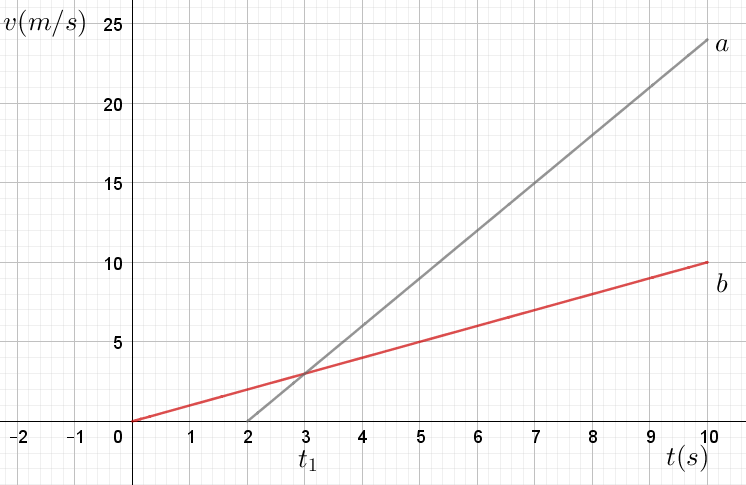
- Deux voitures démarrent du même endroit et roulent sur une même route rectiligne.
- Quelle est celle qui a la plus grande accélération? Justifie.
- Que se passe-t-il à l’instant \(t_{1}\)?
\(\\\)
\(\\\)
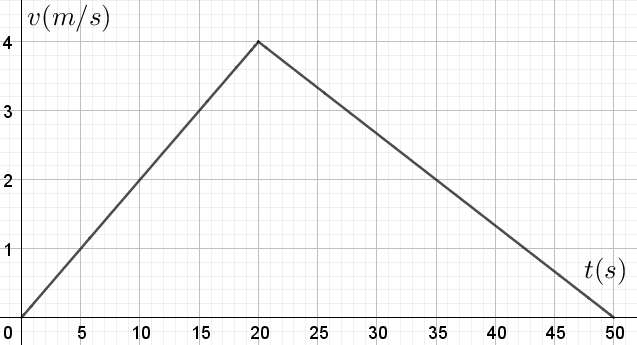
- Le graphique suivant représente 50 secondes du mouvement d’un mobile. Quelle distance a-t-il parcourue au bout des 50s?
Le MRUA: des exercices pour s’entrainer à écrire les équations
- Pour pouvoir décoller, un petit avion doit atteindre 144 km/h.
- Que doit valoir l’accélération constante nécessaire à son décollage sur une piste de 300m ?
- Quelle est la durée de la phase d’élan ?
\(\\\)
- Une voiture aborde la bande de lancement d’une autoroute à 54 km/h. Son conducteur accélère (a = 1,5 m/s²) pour atteindre une vitesse suffisante avant de s’insérer dans le trafic. Combien de temps lui faudra-t-il pour atteindre 108 km/h ?
\(\\\)
- Calculez les accélérations moyennes pour les mobiles suivants :
- Une flèche qui parcourt une distance de 55 cm avant de rompre le contact avec la corde qui la propulse, sachant que dans le même temps, sa vitesse augmente de 0 à 60 m/s.
- Une balle de fusil chassée par le gaz qui se détend dans un canon de 45 cm, sachant que la balle quitte le canon à une vitesse de 720 m/s.
- Une voiture qui heurte un arbre à une vitesse de 90 km/h, si l’avant de la voiture est enfoncé de 25 cm.
\(\\\)
- Une voiture part arrêtée et atteint la vitesse de 22 m/s en 20 s.
- Quelle est son accélération ?
- Combien de temps mettra-t-elle pour passer de 22 à 30 m/s avec la même accélération ?
\(\\\)
- Les freins d’une voiture sont appliqués alors qu’elle roule à 14 m/s ce qui provoque un arrêt après 4 s.
- Quelle est l’accélération ?
- Quel temps aurait-elle mis pour s’arrêter, avec la même accélération, à partir d’une vitesse initiale de 44 m/s ?
- En combien de temps passe-t-elle de 20 à 10 m/s, avec cette accélération ?
\(\\\)
- Un avion décolle à 80 m/s, une vitesse qu’il atteint 35 s après son départ arrêté.
- Combien de temps a-t-il mis pour atteindre la vitesse de 20 m/s ?
- Combien de temps met-il pour passer de 60 à 80 m/s ? Quelle distance parcourt-il pendant cette phase ?
- Quelle longueur minimum la piste doit-elle avoir ?
\(\\\)
- Un bus fait 400 m entre deux arrêts. Il part arrêté et accélère à 1,5 m/s² jusqu’à ce qu’il atteigne une vitesse de 9 m/s. Il continue ensuite à vitesse constante et freine ensuite avec une décélération de -2 m/s² jusqu’au prochain arrêt. Déterminez la durée totale du trajet.
\(\\\)
- Extrait de www.gqmagazine.fr (le 10/01/20). « En Suède, il n’y a pas qu’Ikea ou Volvo, il y a aussi Koenigsegg, un riche entrepreneur qui fabrique des bolides pour rouler à 400 km/h. Alors forcément pour atteindre une telle vitesse de pointe il faut accélérer très fort, ce que la Regera réalise à la perfection puisqu’elle passe de 0 à 100 km/h en 2,5 s. Vous pouvez acquérir ce bolide de 1500ch (V8 hybride) pour 2,1 millions d’euros. Ceci dit, la Bugatti Chiron Sport réalise le même exploit en 2,4s ! Mais elle vous coutera 3,2 millions d’euros. Le roulement de tambour revient toutefois à la Rima CTwo, une voiture croate 100% électrique, de 1914ch et qui est capable de passer de 0 à 100km/h en 1,85 seconde seulement ! » Et ce, pour la modique somme de 2,2 millions d’euros, ce qui en fait notre Maître-achat ! Détermine l’accélération moyenne que ces voitures sont capables de tenir sur le 0-100km/h et détermine la distance qui leur est nécessaire.
\(\\\)
- Un cycliste roulant à 30 km/h cesse de pédaler. Quelle vitesse aura-t-il 20m plus loin, si sa décélération, due aux frottements, est de 0,3m/s²?
\(\\\)
- Calculez la distance de freinage d’un véhicule roulant à 140 km/h. On supposera que nous sommes dans des conditions normales, c’est-à-dire un temps de réaction du conducteur de 0,7s et une décélération de 5 m/s².
Astuce: Durant le temps de réaction, les influx nerveux circulent dans le corps et le conducteur ne freine donc pas encore! Il est donc en MRU durant 0,7s avant d’entamer son MRUD!
\(\\\)
- Un véhicule roule à une certaine vitesse quand, à un instant donné, le conducteur aperçoit un obstacle. Avant d’enfoncer la pédale de frein, un temps de réaction est indispensable, pendant lequel le véhicule parcourt une certaine distance qui peut s’avérer déterminante. On suppose dans cet exercice que le temps de réaction est de 1 seconde. Les tests effectués sur un véhicule de masse 1000 kg (voir document ci-dessous) donnent une idée de ce que peut représenter la distance d’arrêt en fonction de la vitesse du véhicule, en cas de freinage urgent. Ces tests ont été réalisés avec une voiture en parfait état et sur route sèche.

Détermine la valeur de la décélération de la voiture pour une vitesse initiale de 90 km/h.
\(\\\)
- Lorsque le conducteur d’une voiture roulant à 180 km/h sur une autoroute aperçoit au loin un radar de la police, il a un temps de réaction de 0,4 s et décélère ensuite à du 8 m/s². La vitesse maximale toléré étant de 120 km/h, quelle distance ce conducteur aura-t-il parcourue depuis l’observation initiale jusqu’à ce que sa vitesse soit redevenue acceptable (i.e. : 120 km/h) ?
- 86,8 m
- 126,8m
- 106,8m
- 102,8m
- 82,7m
\(\\\)
- Le chauffeur d’un camion roulant à 108 km/h aperçoit soudain un troupeau de caribous à 70 mètres devant lui. Le temps de réflexe du chauffeur est de 0,8s et la décélération maximale de 8 m/s², dans ces conditions, il ne peut pas éviter le troupeau. Quelle sera, en km/h, la vitesse de collision?
\(\\\)
- Lorsqu’un feu rouge passe au vert, une voiture qui était à l’arrêt, démarre avec une accélération constante de 6 m/s². Au même instant elle est dépassée par un camion roulant à une vitesse uniforme de 21 m/s.
- Après quelle distance la voiture rattrapera-t-elle le camion ?
- Quelle vitesse aura-t-elle à ce moment ?
- Représentez graphiquement la distance parcourue ainsi que la vitesse des deux véhicules en fonction du temps.
Astuce: On parle de deux mobiles, il faut donc écrire les équations de l’un \(x_{1}(t)\) et de l’autre \(x_{2}(t)\). Quand les deux véhicules occuperont la même position, on pourra écrire: \(x_{1}(t)=x_{2}(t)\)
\(\\\)
- Deux chiens de chasse aperçoivent, à 5m, du gibier s’éloignant à la vitesse constante de 25km/h. Ils démarrent alors avec une accélération de 1,5m/s². Calculer la durée nécessaire aux chiens pour rattraper leur proie, leur vitesse à cet instant et la distance qu’ils ont dû parcourir. Tracez l’allure du graphique x(t) sur lequel vous superposez les courbes des chiens avec celle du gibier.
\(\\\)
- Une voiture de police de type BMW M5 est arrêtée à un feu rouge. Une moto grille le feu rouge en roulant à une vitesse constante de 90 km/h. La voiture démarre après un temps de réaction de 0,5s; avec une accélération constante de 6 m/s².
- Au bout de combien de temps la police rattrape-t-elle la moto ?
- Quelle est alors la vitesse de la voiture de police en km/h ? (Rmq : la M5 est capable d’atteindre 250 km/h).
\(\\\)
- Un chien aperçoit un chat qui trottine dans sa direction à une vitesse de 8 km/h, alors qu’ils sont à 35m l’un de l’autre. Le chien, fou des chats, accélère dans la direction du chat à un rythme de 5m/s², alors que le chat, inquiet de la situation, réduit timidement son allure à un rythme de -0,5m/s². Le chat a-t-il le temps de s’arrêter (et éventuellement de se sauver dans l’autre sens) avant que le chien ne parvienne à sa hauteur ? Si non, déterminez à quel endroit et après combien de temps le chien est parvenu à hauteur du chat.
\(\\\)
Rmq : pour s’entrainer à acquérir tous les bons réflexes (signes des composantes scalaires des vecteurs vitesse et accélération), on mettra le chat dans le sens du référentiel et le chien dans le sens opposé.
\(\\\)
- Un conducteur A circulant à 120km/h sur l’autoroute, aperçoit un conducteur fantôme F (circulant à contre-sens) roulant à 90km/h, alors qu’il est à 250m de lui. On considère cet instant comme l’origine des temps t=0. Après un temps de réaction de 0,5s ; le conducteur A freine à un rythme de 9m/s². Le conducteur fantôme F s’aperçoit de la situation également, mais, seulement à l’instant t=1s. Il freine alors à raison de 7m/s². La collision est-elle évitable ? Si non, à quelle vitesse a-t-elle lieu ? Si oui, où s’arrêtent les deux voitures?
\(\\\)
Si tu sais faire cet exercice, tu es paré pour tout le reste! Il combine temps de réaction, vitesses opposées et retard! Bref, de quoi bien s’amuser!
\(\\\)
- Sur une autoroute 2 voitures roulent sur la même file avec une vitesse de 40m/s. Le pare chocs avant A de la seconde voiture est à 40m derrière le pare chocs arrière B de la première voiture. Le véhicule B freine avec une décélération de 5 m/s². Le véhicule A distrait freine 2s après avec la même décélération. Après combien de temps a lieu la collision ? Quelle est alors la vitesse de chacune des deux voitures ?
\(\\\)
Exercices corrigés pas à pas disponibles ici! Fascicule reprenant:
- 3 pages de synthèse sur TOUT ce qu’il faut ABSOLUMENT comprendre avant de se lancer tête baissée dans les exercices sur le MRUA (et de perdre son temps) !
- Les 29 exercices ci-dessus corrigés dans les moindres détails en 41 pages!
Bref, l’équivalent de plus de 10 heures de cours pour moins de 30€ !!!
Clique sur le bouton « Acheter » ci-dessous…

Voici un exemple d’exercice résolu dans ce document:




















À propos de l’auteur