Bonjour à toutes et à tous,
Aujourd’hui, je vous propose de faire la différence entre les notions de vitesse scalaire et de vitesse vectorielle ainsi qu’entre les vitesses (vectorielles) moyenne et instantanée.
Dans la vie de tous les jours, on parle souvent de vitesse. Et bien ça, c’est un truc qui m’ennuie dans mon labo de physique! Pourquoi diable me direz-vous? Et bien, simplement parce que la vitesse du physicien est bien plus qu’une simple valeur qui, par dessus le marché, est souvent mal prononcée! En effet, dans la vie de tous les jours vous dites: « Je me suis fait flashé à 150 kilomètre-heure »! Mais quelle horreur!!! Le kilomètre-heure, qui devrait être noté « km.h », N’EXISTE PAS! Une vitesse, c’est un rapport entre une distance (exprimée en km) et le temps nécessaire pour la parcourir (exprimé en h éventuellement), ce qui nous donne donc des « kilomètres PAR heure », notés « km/h »! Rien à voir avec le km.h! Bannissez donc cette horreur de vos bouches jeunes gens!
Ceci étant dit, je vous invite à découvrir la vraie vitesse, celle du physicien! Let’s go!
En physique, on distingue la notion de vitesse de celle de vitesse scalaire.
1. La vitesse scalaire ou la « speed » des anglophones
La vitesse scalaire, c’est la vitesse de « Monsieur tout le monde »! Comme son nom l’indique, c’est une notion purement scalaire qui donne le rapport entre la distance totale parcourue, notée \(d\) et le temps nécessaire pour la parcourir, noté \(\Delta t\). Il s’agit donc simplement d’une valeur (un scalaire pur et dur) sans aucune notion de direction.
\(\\\)
\begin{equation}
\ v_{scalaire} = \frac{d}{\Delta t}
\tag{1}
\end{equation}
C’est pratique pour une discussion entre potes mais autant vous dire de suite qu’on ne l’utilisera pas beaucoup en classe de physique…
2. La vitesse, la vraie, celle du physicien ou la « Velocity » des anglophones
2.1. La vitesse moyenne
Alors là, les petits amis, on change de monde! Du monde scalaire, on fait notre grande entrée dans le monde vectoriel! Parce que, la vitesse, Mesdames et Messieurs est un vecteur, mieux vaut ne pas l’oublier! Pour faire simple, la vitesse du physicien n’a pas seulement une valeur mais également une direction (horizontale, verticale, oblique) et un sens (N,S,…)!
Dans un article précédent, nous avons déjà défini ce vecteur. Si votre mémoire vous fait défaut, la définition est disponible ici au paragraphe 2.
Nous sommes donc au point avec la notion de vitesse! Que vient faire l’adjectif « moyenne » alors? Il vient simplement du fait que la vitesse est considérée sur un intervalle de temps relativement grand. Regardons plutôt la trajectoire suivante.
\(\\\)
\(\\\)
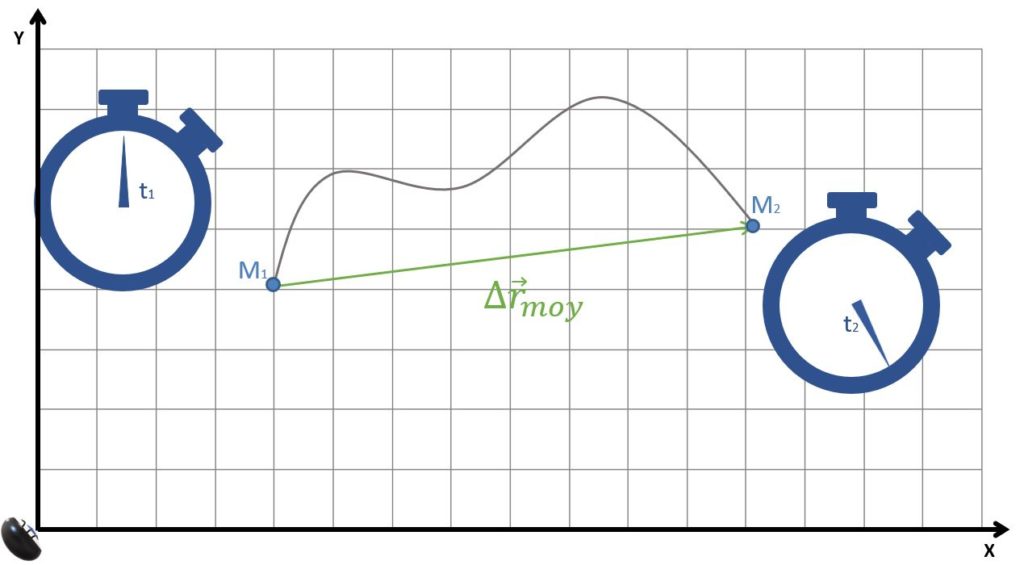
Soit \(M_{1}\) la position atteinte par un mobile dans le référentiel (x,y) à l’instant \(t_{1}\) et \(M_{2}\) la position atteinte par ce même mobile à l’instant \(t_{2}\). Le vecteur déplacement (ou variation de position) entre ces deux points est représenté sur la trajectoire, il s’agit du vecteur \(\Delta \overrightarrow{r}_{moy} \).
Rappelons la définition du vecteur vitesse et ajoutons l’indice « moy » pour montrer que l’intervalle de temps considéré est long:
\(\\\)
\begin{equation}
\ \overrightarrow{v}_{moy} = \frac{\Delta \overrightarrow{r}_{moy} }{\Delta t_{ }}
\tag{2}
\end{equation}
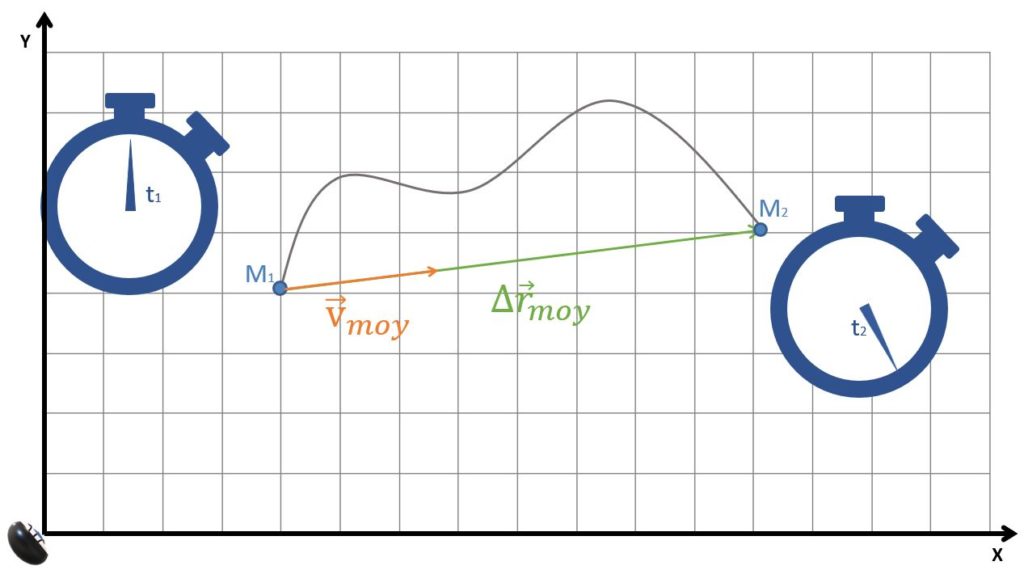
Nous savons que les deux vecteurs de cette définition ont le même sens et la même direction étant donné que le scalaire \(\Delta t\) est toujours positif. Nous pouvons donc ajouter à la trajectoire le vecteur vitesse moyenne. Remarquons que ce vecteur a une direction quelconque par rapport à la trajectoire.
\(\\\)
Pour connaitre la norme du vecteur vitesse moyenne, étant donné que les vecteurs \(\overrightarrow{v}_{moy}\) et \(\Delta \overrightarrow {r}_{moy}\) ont même direction, on pourra simplement écrire:
\(\\\)
\( \lVert\overrightarrow{v}_{moy}\lVert = \frac{\lVert\overrightarrow{\Delta r}_{moy}\lVert}{\Delta t} \)
Et on remarque que la vitesse moyenne a les dimensions d’une longueur sur un temps, elle est donc exprimée en \(m/s\).
\(\\\)
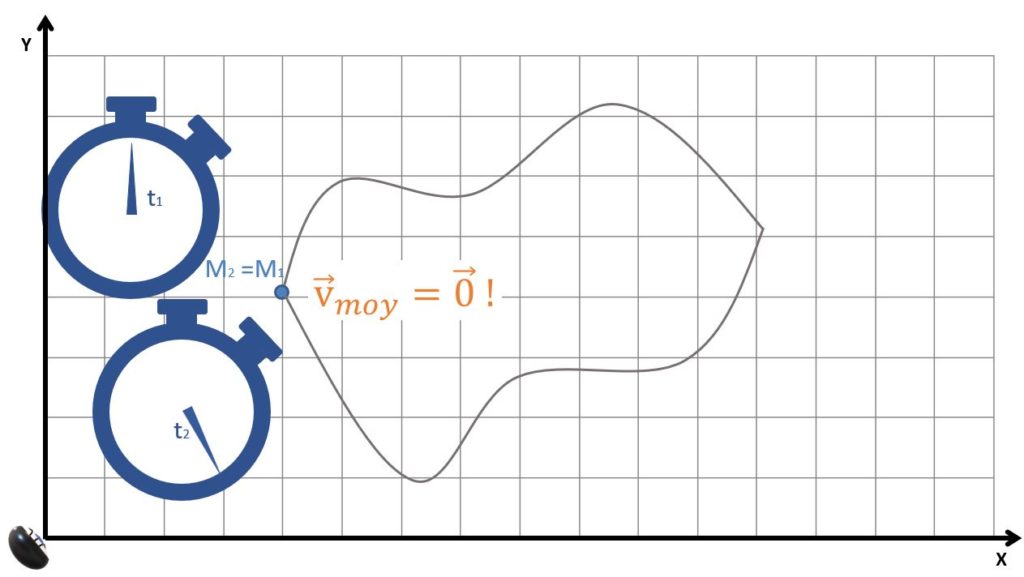
Il y a quelque chose d’amusant avec cette notion. Imaginez que le mobile parcourt une trajectoire fermée et revienne exactement à son point de départ. Dans ce cas, le vecteur déplacement moyen est nul (puisque les positions initiale et finale sont identiques) et il en est de même pour la vitesse moyenne! Même si le mobile a effectué la courbe à très grande vitesse, sa vitesse moyenne est nulle! Remarquez que les anglophones se sont facilité la vie! Pendant que nous devons dire: « La vitesse scalaire est importante mais la vitesse moyenne est nulle », ils diront: « Speed is high but Velocity is zero! » C’est plus clair, non?
2.2. La vitesse instantanée
La vitesse moyenne n’est pas d’une grande utilité quand on veut caractériser le mouvement d’un objet. Il est en effet souvent nécessaire de connaitre la vitesse d’un mobile à un instant précis, plutôt que la vitesse moyenne dans un intervalle de temps donné. Pour ce faire, la vitesse instantanée nous est d’une aide précieuse! Elle consiste à considérer le point \(M_{2}\) infiniment proche du point \(M_{1}\). Les instants \(t_{1}\) et \(t_{2}\) sont donc très proches l’un de l’autre et l’intervalle de temps \(\Delta t\) ridiculement petit. Concrètement, cela correspond au flash radar qui mesure la vitesse de votre voiture à un instant bien précis! En termes mathématiques, on dira que \(\Delta t\) tend vers zéro, ce qui se note \(\Delta t \rightarrow 0\). On peut donc réécrire l’équation (2) et la transformer en vitesse instantanée, ou en vitesse tout court puisque c’est elle qui est la plus célèbre en physique:
\(\\\)
\begin{equation}
\ \overrightarrow{v}_{inst} = \overrightarrow{v} = \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{r}}{\Delta t_{ }}
\tag{3}
\end{equation}
J’avoue que de prime abord, ça peut paraitre indigeste, mais il suffit d’apprendre à lire les mathématiques! Si, en regardant cette expression, vous vous dites: « La vitesse instantanée, c’est la limite, quand delta t tend vers zéro, du rapport entre le vecteur déplacement et l’intervalle de temps nécessaire à le réaliser ». Si vous comprenez exactement cette phrase, alors, vous imaginez sans soucis, qu’il suffit de prendre, dans la définition du vecteur vitesse, un intervalle de temps ridiculement petit! Bref, à la limite, un seul instant!
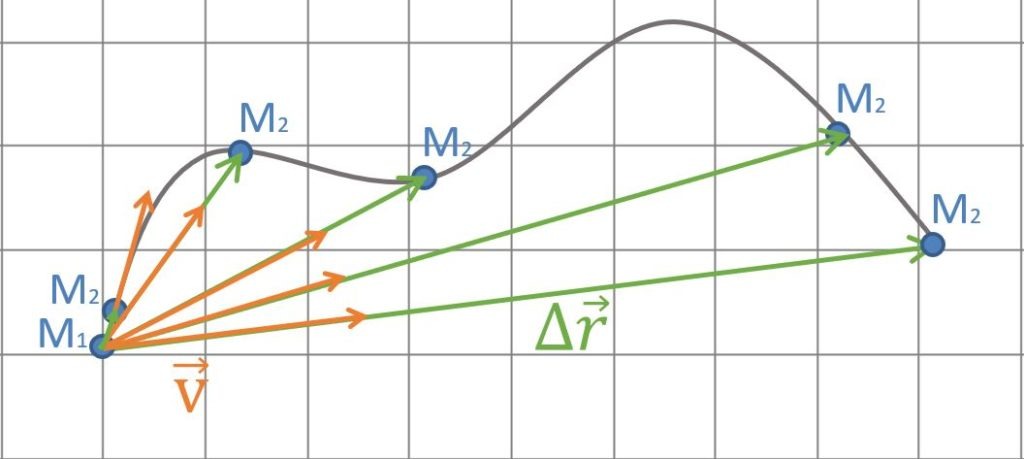
Qu’arrive-t-il au vecteur vitesse au fur et à mesure que l’intervalle de temps diminue, càd que \(M_{2}\) se rapproche de \(M_{1}\)?
\(\\\)
\(\\\)
Le vecteur vitesse devient progressivement tangent à la trajectoire. Concrètement, vous pouvez vous représenter cela en imaginant un vecteur vitesse (une flèche quoi) enfoncée dans le capot avant de votre voiture. La voiture tourne? Et bien le vecteur vitesse tourne avec elle! C’est pas plus compliqué que cela! Exactement comme sur la représentation suivante, gardez toujours bien cela en tête!

\(\\\)
Conclusion
Le vecteur vitesse instantanée est défini par la relation suivante:
\(\\\)
\begin{equation}
\ \overrightarrow{v} = \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{r}}{\Delta t_{ }}
\tag{4}
\end{equation}
\(\\\)
Ce vecteur est toujours tangent à la trajectoire .
3. Le vecteur vitesse dans un référentiel à une dimension
Les cours de physique débutent toujours avec l’étude des mouvements rectilignes (les fameux MRU et MRUA). Comme leur nom l’indique, étant donné que le mouvement ne peut se faire qu’en ligne droite, un seul axe suffit à le caractériser. Que deviennent le vecteur déplacement \(\Delta \overrightarrow{r}\) et le vecteur vitesse \(\overrightarrow{v}\)? Alors, là, on a besoin de faire un petit détour…
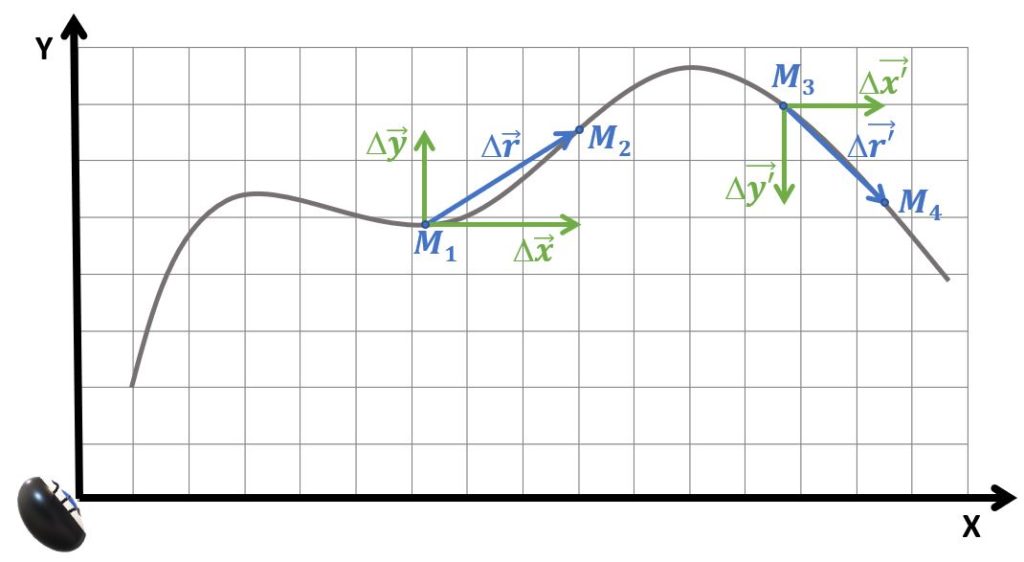
Petit rappel: dans un référentiel à deux dimensions, le vecteur variation de position (ou déplacement) \(\Delta \overrightarrow{r}\); possède deux composantes selon les axes X et Y: on les note \(\Delta\overrightarrow{x}\) et \(\Delta\overrightarrow{y}\).
La figure ci-dessous montre deux vecteurs déplacements différents. Dans le premier cas, entre les points \(M_{1}\) et \(M_{2}\), les deux composantes du vecteur déplacement ont une composante scalaire positive puisque les vecteurs sont dirigés dans le sens de l’axe (X ou Y). Par contre, dans le second cas de figure, entre les points \(M_{3}\) et \(M_{4}\), la composante scalaire du vecteur \(\Delta\overrightarrow{y’}\) est négative puisqu’elle est opposée au référentiel.
\(\\\)
Cela aura comme conséquence que la composante scalaire du vecteur \(\overrightarrow{v_{y}}\) sera elle aussi négative.
La norme du vecteur vitesse restera bien entendu positive puisqu’elle est donnée par la relation \(\\\)
\( \lVert\overrightarrow{v}\lVert = \sqrt{(v_{x})^2+(v_{y})^2}\)
\(\\\)
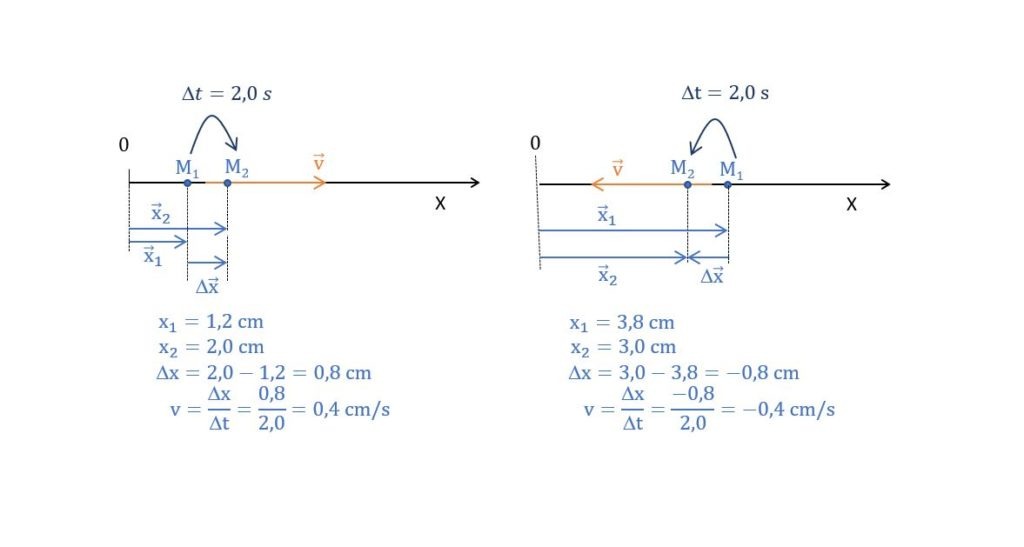
Dans un mouvement à une seule dimension, étudié le long d’un référentiel X, les vecteurs déplacement et vitesse n’ont évidemment qu’une composante le long de ce référentiel X. Le vecteur position se notera donc \(\overrightarrow{x}\) (au lieu de \(\overrightarrow{r}\)) et le vecteur variation de position (ou déplacement) \(\Delta \overrightarrow{x}\) (au lieu de \(\Delta \overrightarrow{r}\)). On peut également rencontrer deux cas de figure: soit le mouvement se fait dans le sens du référentiel et les vecteurs déplacement et vitesse auront une composante scalaire positive; soit le mouvement se fait dans le sens opposé au référentiel et ces vecteurs auront une composante scalaire négative. C’est ce qu’illustre la figure suivante. \(\\\)
4. Ce que je dois retenir…
- La vitesse scalaire me donne le rapport de la distance totale parcourue et du temps nécessaire à parcourir cette distance. C’est une notion très peu utilisée en physique.
- La vitesse moyenne est un vecteur qui possède une orientation quelconque par rapport à la trajectoire. Sa valeur est donnée par le rapport entre la composante scalaire du vecteur déplacement et le temps nécessaire à le réaliser. L’intervalle de temps peut prendre n’importe quelle valeur.
- La vitesse instantanée est également un vecteur mais il est TOUJOURS tangent à la trajectoire. Sa valeur est donnée par le rapport entre la composante scalaire du vecteur déplacement et le temps nécessaire à le réaliser. L’intervalle de temps doit nécessairement être le plus petit possible. Idéalement, il doit tendre vers zéro.
- Les composantes scalaires des vecteurs déplacement et vitesse peuvent être négatives, cela correspond simplement à un mouvement qui se produit dans le sens opposé au référentiel d’étude. En effet, dans ce cas, les vecteurs déplacement et vitesse sont de sens opposé à celui du référentiel!
Il est très important de bien comprendre ces notions et de savoir exactement ce que représentent les différents vecteurs afin que les exercices de construction du vecteur vitesse soient réalisables! Bon travail et à bientôt!
P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant au bas de cette page. Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile. Merci!







Et dire qu’à une époque je maîtrisais ces concepts sur le bout des doigts.
J’ai bien ralenti depuis…
Merci Julie pour cet article qui m’a rafraîchit la mémoire à une vitesse grand V !
Olivier
PS : à partir de maintenant et pour longtemps, soit à l’instant t1, je dirai « kilomètres par heure »…