Exercice 1
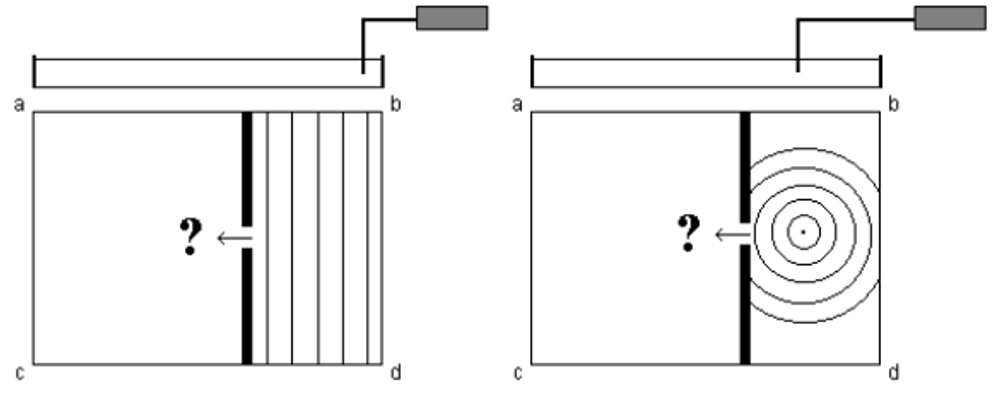
Que se passe-t-il lorsqu’une onde (plane ou circulaire) rencontre une petite digue possédant une ouverture comme représenté sur le schéma ci-dessous ?
Exercice 2
Étude sommaire de la houle. (Bac Réunion 2006)
La houle prend naissance sous l’effet du vent loin des côtes. Un vent de \(65 km.h^{-1}\) engendre une houle dont les vagues font 1 mètre de hauteur. Ces vagues sont espacées de 230 mètres. Une vague remplace la précédente après une durée de 12 secondes.
- Calculer la vitesse de déplacement des vagues à la surface de l’océan.
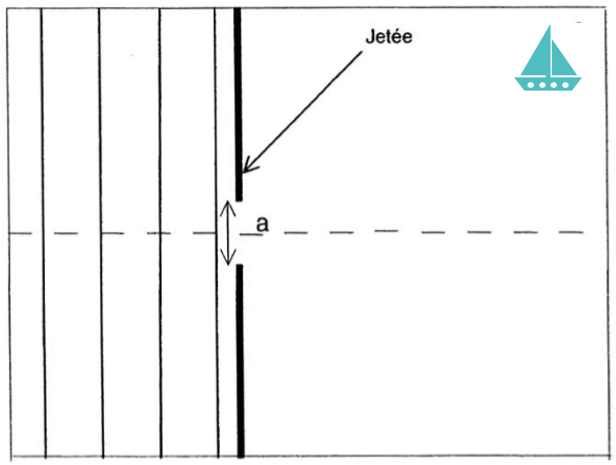
- Cette houle arrive sur un port dont l’ouverture entre deux jetées a une largeur de 150 m. Un bateau est stationné au fond du port comme indiqué sur le schéma ci-dessous. Ce bateau risque-t-il de ressentir les effets de la houle ? Justifier la réponse.
Exercice 3
Un capteur fixé sur la bouée n°1 permet d’enregistrer le mouvement vertical de la surface de la mer dû à la houle. Ce capteur a permis de réaliser l’enregistrement présenté ci-dessous, débutant à un instant choisi comme origine (t=0).
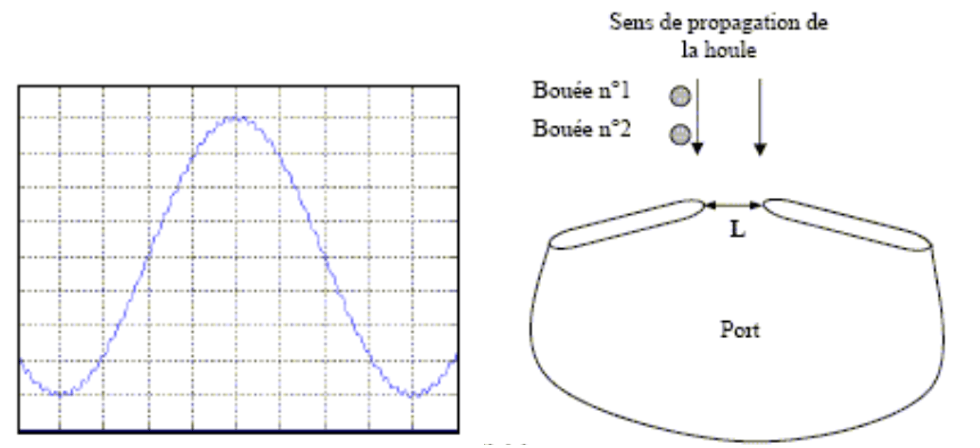
Sensibilité du capteur : 2,0 mV/cm
Sensibilité verticale de l’enregistreur : 50 mV/division
Base de temps de l’enregistreur : 0,50 s/division
- Quelle est la période (temporelle) de cette houle ?
- On observe que l’écart d entre les sommets de deux vagues successives est de 24 m. Quelle est la vitesse de propagation de cette houle ?
- Quelle est l’amplitude de cette houle ?
- La houle atteint l’entrée d’un port, limité par deux digues séparées par un passage de largeur L=48 m. Quel phénomène se produit alors? Quelle est la zone du port qui ne sera pas abritée de la houle ? Représenter qualitativement cette zone sur le schéma, et préciser la relation qui permet de calculer l’angle correspondant à la limite entre la zone abritée et la zone non abritée. Calculer cet angle.
Exercice 4
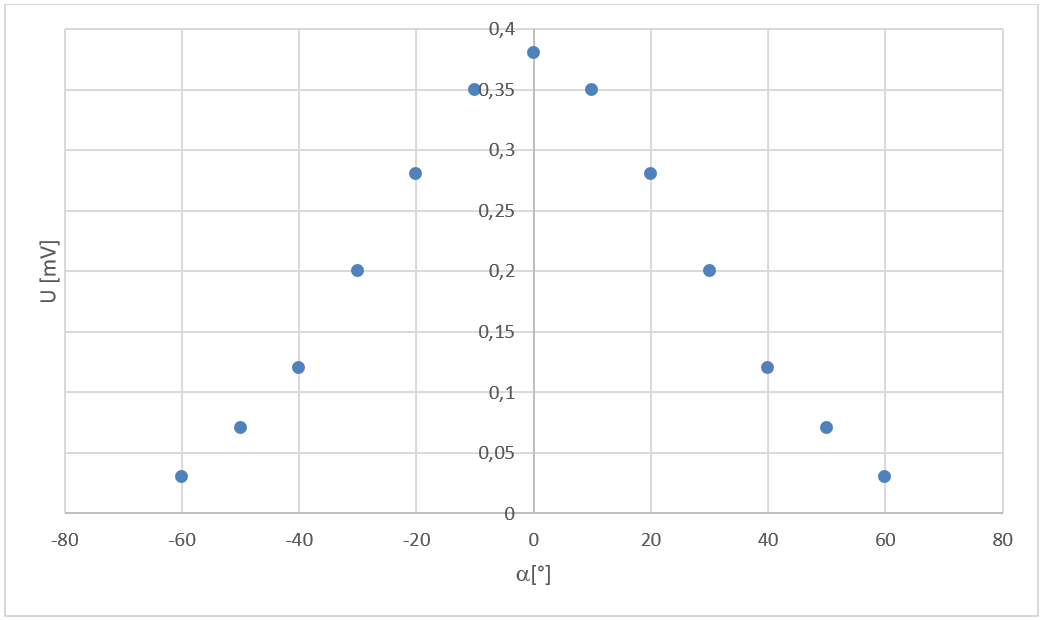
Un émetteur envoie des ultrasons en continu. Un récepteur est placé à 30 cm de cet émetteur, le point de réception faisant un angle α avec l’axe de l’émetteur. Le récepteur est relié à la voie X d’un oscilloscope. On mesure sur l’oscilloscope l’amplitude électrique U des ondes reçues pour une série de valeurs de l’angle α.
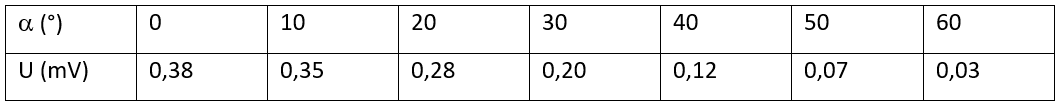
Si on trace U en fonction de \(\alpha\), on obtient le graphique suivant :
Pour un angle particulier, on obtient cet oscillogramme (5,0 µs/division) :
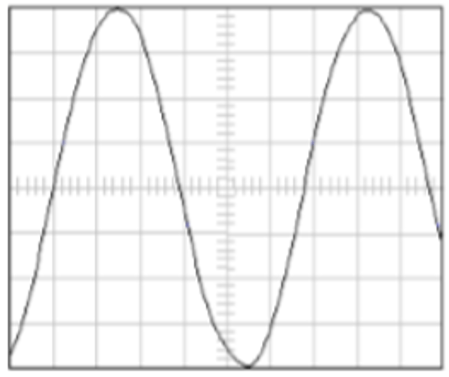
- Quelle est la longueur d’onde des ultrasons émis ?
- Sur le graphique précédent, représente les variations de U en fonction de \(\alpha\) entre -60° et +60°.
- Compare les deux courbes. Quel phénomène est mis en évidence ? Est-ce cohérent avec la théorie que tu as reçue en classe ? Explique.
On place ensuite devant l’émetteur une fente de 4 mm de largeur et on effectue la même série de mesure. Voici les résultats obtenus.
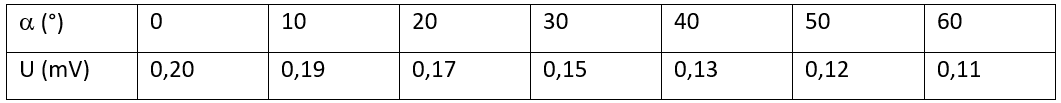
Exercice 5
Une lumière de 680 nm de longueur d’onde tombe sur une fente de largeur 0,06 mm. On observe la figure produite sur un écran situé à 1,8m.
- Quelle est la largeur du pic central ?
- Quelle est la distance sur l’écran entre les minima de premier et de deuxième ordre ?
Exercice 6
Lorsque la lumière de longueur d’onde 589 nm émise par des vapeurs de sodium éclaire une fente simple, le pic central de diffraction sur l’écran a une largeur de 3 cm. Quelle serait la largeur du pic avec la raie de 436 nm émise par des vapeurs de mercure si l’écran se trouve à 2 mètres de l’ouverture ?
Exercice 7
Soit une fente simple éclairée par la lumière verte émise par les vapeurs de mercure, de 546 nm de longueur d’onde. Le pic central de diffraction a une largeur de 8 mm sur un écran situé à 2m de la fente. Quelle est la largeur de la fente ?
Exercice 8
Dans une figure de diffraction produite par une fente simple, le premier et le deuxième minimum sont distants de 3 cm sur un écran situé à 2,8m de la fente. Déterminer la largeur de la fente sachant que la lumière a une longueur d’onde de 480 nm. Une approximation est nécessaire pour réaliser cet exercice, il faudra l’expliquer.
Exercice 9
On dispose d’un laser hélium-néon de longueur d’onde \(\lambda=632,8 \, nm\) et de puissance \(P = 2,0 \, mW\). On interpose une fente fine verticale entre le laser et un écran E. Sur l’écran, on observe, dans la direction perpendiculaire à la fente, une tache lumineuse centrale de largeur d nettement supérieure à la largeur a de la fente, ainsi qu’une série de taches lumineuses plus petites de part et d’autre de la tache centrale. La distance entre la fente et l’écran est \(D=1,60 \, m\).
- Faire un schéma de l’expérience et nommer le phénomène observé.
- Lors de deux expériences, on mesure pour la tache centrale : une longueur \(d_{1}=5,0 \, cm\) avec une fente de largeur \(a_{1}=0,04 \, mm\) et une longueur \(d_{2}=2,0 \, cm\) avec une fente de largeur \(a_{2}=0,10 \, mm\). Montrer que ces résultats sont en accord avec la théorie.
- On remplace la fente fine par un cheveu tendu verticalement sur un support. Pour la même distance D du fil à l’écran, on observe une figure analogue à celle obtenue avec la fente et on mesure d=2,6 cm pour la largeur de la tache centrale. En admettant que la théorie reste valable pour le cheveu, calculer son diamètre a.
- On utilise maintenant un laser de même longueur d’onde \(\lambda = 632,8 nm\) mais de puissance \(P = 1,0 \, mW\). Quelle est, pour le cheveu, la largeur de la tache lumineuse centrale ? Choisir en justifiant, la bonne réponse parmi les propositions suivantes : a) 1,3 cm b) 2,6 cm c) 5,2 cm.
Exercice 10
Lors d’une expérience de diffraction, on relève l’intensité d’une onde lumineuse diffractée par différentes fentes rectangulaires de largeur \(a_{1} = 0,2 mm, \, a_{2} = 0,5 mm \; et \; a_{3} = 0,1 mm\). Les courbes présentant l’évolution de l’intensité en fonction de l’angle sont données dans la figure ci-dessous (les échelles ne sont respectées). La longueur d’onde dans le vide de la radiation monochromatique utilisée est égale à 633 nm, et la célérité des ondes lumineuses dans l’air est \(c= 3,00.10^{8} m/s\). \(\theta\) est la demi-largeur de la tache centrale.
– Quelle est la fréquence de l’onde diffractée par les fentes ?
– Quelle courbe correspondant à la fente n°1 ? à la fente n° 2 ? à la fente n° 3 ?
– Quelle est la largeur de la tache centrale de diffraction obtenue sur un écran situé à la distance D=2,5 m de la fente 1?Merci de liker cet article si ce travail t’a été utile. Si tu souhaites le pdf des exercices corrigés, n’hésite pas à m’envoyer un mail ou à laisser un commentaire.
Bon travail!
Merci d'avoir lu cet article!
En complément, vous êtes libre de recevoir gratuitement mon livre:
"7 outils mathématiques indispensables pour tout comprendre en physique!" qui vous montre notamment:
Partager l'article:- 22Partages
22
