Qu’est-ce qu’un référentiel en physique?

Un référentiel en physique, est un solide, un point de l’espace par rapport auquel on repère un mouvement. Ce point particulier est associé à un chronomètre qu’on décide de déclencher (en physique, on dit qu’on définit la date t=0) à un instant particulier. On utilise généralement un repère galiléen, mais on reparlera de cette particularité plus tard. Pour l’instant, je te propose simplement de réaliser que « le référentiel en physique », c’est un nom bien compliqué pour une notion au final très simple.

Les trajectoires

Il est impossible de caractériser un mouvement sans dire d’abord dans quel référentiel on travaille. La preuve en images !

La fig.1 montre la photographie d’un bombardement. Cette photo est prise d’un avion qui se trouve à côté de celui qui largue les obus et qui vole à la même vitesse. C’est donc lui notre référentiel! Depuis cet avion, on voit les obus tomber à la verticale, la trajectoire de ces derniers est donc une ligne droite.

Imaginons le même avion observé depuis le sol. Le sol devient donc notre nouveau référentiel d’étude. Nous observerions ceci :

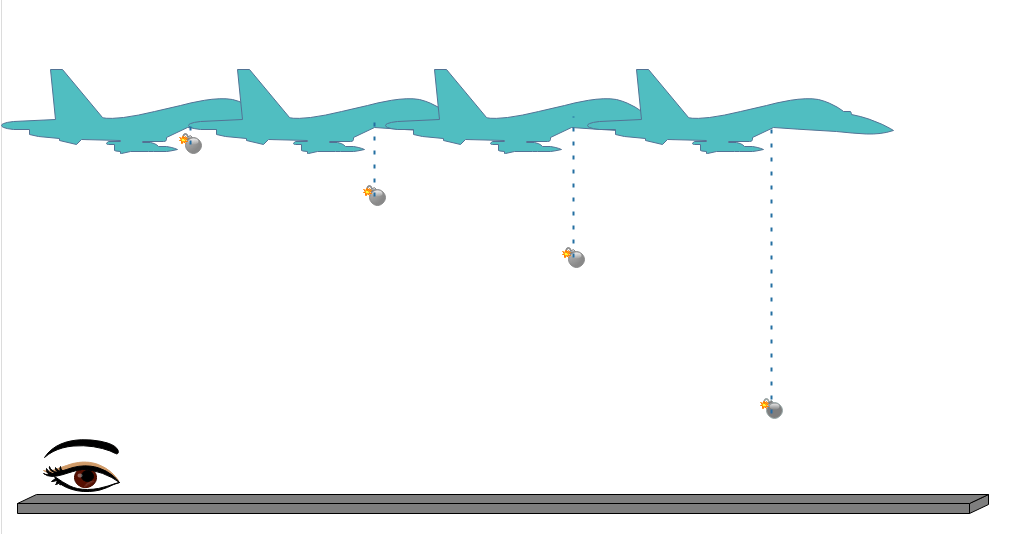
Les traits pointillés guident l’œil pour montrer que la bombe se trouve toujours exactement en-dessous de l’avion comme nous le prouve la photographie de la Fig.1 (ce qui est logique puisque la bombe possède la même vitesse horizontale que lui). Dès lors, depuis le sol, la trajectoire des bombes est une parabole.
Regardez un film de guerre et vous verrez des trajectoires d’obus fondamentalement différentes en fonction de la prise de vue, càd en fonction de l’endroit où se trouve la caméra.
 

Allez maintenant le début de cette vidéo animation, elle vous montre le mouvement d’une balle dans le référentiel terrestre et dans le référentiel d’un train en mouvement. Ces exemples montrent à quel point il est inutile de vouloir décrire un mouvement si on ne précise pas d’abord où se trouve la caméra (le référentiel) qui observe le mouvement. En physique, cette notion de caméra s’appelle le référentiel. Il s’agit d’un système de 3 axes orthonormés à partir desquels on repère les positions d’un corps en mouvement. Tout se passe donc comme si la fameuse caméra était posée à l’origine du système (0,0,0). A ce système d’axes, on ajoute également un chronomètre qui nous donnera l’information « temps » pour déterminer des vitesses!

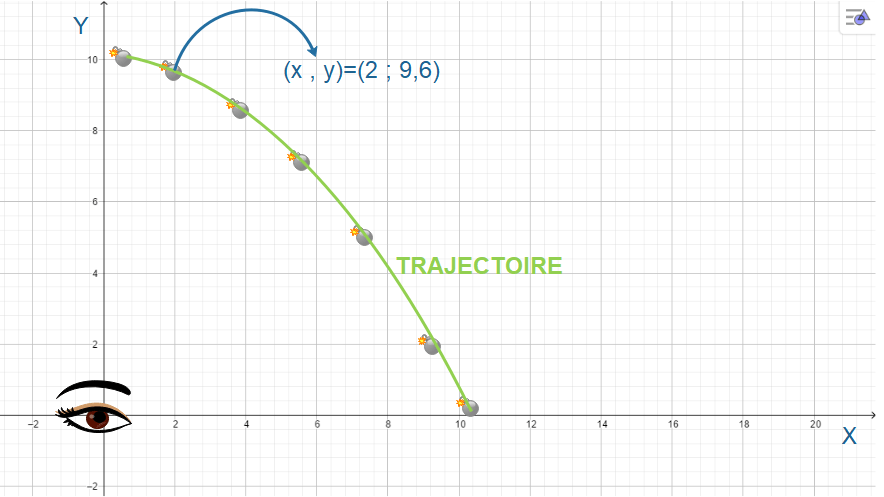
Pour faire simple, nous prendrons souvent un référentiel à deux dimensions (X,Y) seulement. Cela signifie donc que la caméra n’a le droit de regarder que dans un plan, l’œil peut regarder en bas et en haut (le long de l’axe Y) ; en avant et en arrière (le long de l’axe X), mais n’a pas le droit de regarder sur les côtés (le long de l’axe Z). Nous étudierons donc des mouvements plans.

Les vecteurs position et déplacement dans un référentiel en physique

L’étude de ces mouvements impose quelques connaissances vectorielles, dont un rappel fondamental sera trouvé dans l’article suivant: Les vecteurs: du monde mathématique au monde physique.
Si on travaille dans un référentiel (X,Y), on pourra repérer les positions successives ( \( M_{1} \ et \ M_{2}\)) d’un mobile en mouvement à l’aide des vecteurs position \(\overrightarrow{r_{1}} \ et \ \overrightarrow{r_{2}} \), dont les origines se trouvent à l’origine du référentiel (0,0) et l’extrémité à la position occupée par le mobile. On définit alors naturellement le vecteur variation de position (ou déplacement) de la façon suivante: \(\Delta\overrightarrow{r}=\overrightarrow{r_{2}} – \overrightarrow{r_{1}} \). On voit en effet que, si on ajoute l’opposé du vecteur \(\overrightarrow{r_{1}} \), soit \(-\overrightarrow{r_{1}} \), à \(\overrightarrow{r_{2}} \), on trouve \(\Delta\overrightarrow{r}\), comme le montre la Fig.4.

Une chose fondamentale à observer, est que le vecteur déplacement est indépendant du référentiel choisi . Si on change de référentiel (Fig.5), on pose maintenant notre œil sur la droite de l’écran et on observe la réalité dans le référentiel (X’,Y’), les vecteurs position changent et deviennent \(\overrightarrow{r’_{1}} \ et \ \overrightarrow{r’_{2}} \), mais le vecteur déplacement \(\Delta\overrightarrow{r} \) qui sera défini par \(\Delta\overrightarrow{r} =\overrightarrow{r’_{2}} – \overrightarrow{r’_{1}} \), est strictement identique au vecteur déplacement défini dans le premier référentiel (X,Y).
Si on ajoute l’opposé du vecteur \(\overrightarrow{r’_{1}} \), soit \(-\overrightarrow{r’_{1}} \), à \(\overrightarrow{r’_{2}} \), on trouve \(\Delta\overrightarrow{r}\)

Le vecteur déplacement étant indépendant du référentiel choisi, on a le droit de travailler dans n’importe quel référentiel! Et c’est ça qui est bien! En pratique, je vous apprendrai à choisir, en fonction des cas d’étude, le référentiel le plus judicieux pour que les développements mathématiques soient les plus simples possibles!
Remarquons enfin que le vecteur déplacement nous permettra de définir le vecteur vitesse moyenne et le vecteur vitesse instantanée, suite au prochain épisode!

Je retiens:

Un référentiel, c’est un objet ou un point de l’espace à partir duquel je tire trois axes orthonormés le long desquels je peux repérer la position d’une masse en mouvement. A ce référentiel spatial, j’ajoute un chronomètre et je choisis la date t=0, càd le moment auquel j’enclenche le chrono. J’ai alors tout ce qu’il faut pour étudier le mouvement d’une masse et caractériser sa vitesse. Le vecteur déplacement étant indépendant du référentiel dans lequel on travaille, on peut choisir n’importe quel référentiel!

A bientôt!