Recevez gratuitement
mon livret!
Bonjour à toutes et à tous,
pour ceux d’entre vous qui peinent à résoudre des exercices plus complexes (avec des forces de frottement par exemple), voici deux exercices basiques résolus à l’aide du principe fondamental de la dynamique (noté par la suite PFD): \(\Sigma \overrightarrow{F} = m.\overrightarrow{a}\)
Que nous dit le principe?
A cette question, mes élèves ont l’habitude de répondre: « F=m.a » ou encore (un peu mieux): « La somme des forces est égale à la masse fois l’accélération »! Okay, c’est un bon début, mais même ma grand-mère aurait pu dire ça! Ce que vous devez voir (et surtout comprendre) derrière cette relation, c’est ceci:
Lorsqu’une force résultante (\(\Sigma \overrightarrow{F}\)) agit sur une masse (\(m\)), elle lui communique une accélération (\(\overrightarrow{a}\)) qui possède même direction et même sens (puisque les deux vecteurs de la relation \(\Sigma \overrightarrow{F} = m.\overrightarrow{a}\) sont reliés par un scalaire positif: m). Ceci étant compris, comme les vecteurs ont même direction, on peut sans aucun problème écrire la relation de façon scalaire: \(\Sigma F=m.a\). Dès lors, on trouvera l’intensité de l’accélération en divisant la force résultante [en N] par la masse sur laquelle elle agit [en kg].
I. Comment ne pas se planter en identifiant les forces?
Alors là, il faut (pour une fois), ne surtout pas risquer l’originalité et s’en tenir au processus suivant:
- Identifier la plus célèbre d’entre toutes: la force poids (pesanteur, gravifique, de gravitation…) Appelez-la comme vous voulez, mais ne l’oubliez pas!
- Est-ce qu’il y a des forces de frottement? C’est le cas si l’objet glisse (frottement cinétique) ou s’il a tendance à glisser parce qu’il est maintenu en équilibre sur un plan incliné par exemple (frottement statique).
- Qui touche la masse que vous étudiez? J’ai l’habitude de dire à mes élèves: « Ne vous prenez pas pour Dieu »! Si vous ne touchez pas un objet, vous ne pouvez pas agir (ou exercer une force) sur lui! Pourtant, tous les joueurs de foot sont convaincus que le ballon avance sur le terrain grâce à la force exercée par leur pied! Que nenni! Impossible pardi! Le pied ne touche plus le ballon? Et bien, il n’exerce plus aucune force sur lui! Point à la ligne! Si le ballon continue à avancer, c’est grâce à la vitesse (ou à l’énergie cinétique) qui lui a été communiquée par le travail de la force de votre pied (oui, quand même!) pendant le (très) bref instant qu’a duré le contact pied/ballon!
Ce troisième point pose parfois problème alors qu’il ne devrait pas. La question est très simple: qui touche la masse?
- Une paroi sur laquelle la masse prend appui? Il y a une réaction normale (càd perpendiculaire) de la part de la paroi. On la note généralement \(\overrightarrow{F_{N}}\) ou encore \(\overrightarrow{R_{N}}\) mais aussi \(\overrightarrow{N}… \)
- Un fil tendu? Et bien il y a une force de tension! \(\overrightarrow{F_{T}}\) ou \(\overrightarrow{T}\) tout court!
- Une main? Et bien il y a une force musculaire! \(\overrightarrow{F_{m}}\) par exemple.
Si vous savez déjà ça, vous irez loin!
II. L’utilité d’un référentiel bien choisi!
Bien choisir son référentiel (càd poser ses axes X et Y), c’est une étape cruciale! Si vous mettez le référentiel n’importe comment, vous risquez de vous retrouver (inutilement) avec des accélérations selon les deux directions et alors là, bonjour la galère!
Sauf mention contraire, on choisit TOUJOURS le référentiel X dans le sens du mouvement! Pourquoi? Pour la simple (et excellente raison) que dans ce cas, la composante scalaire du vecteur vitesse est positive et que la composante scalaire de l’accélération est positive en cas d’accélération; et négative en cas de décélération. Et c’est bien plus simple pour tout le monde! (Si vous n’en êtes pas convaincus, allez voir cet article!).
III. Y’a plus qu’à … appliquer le principe fondamental de la dynamique!
Un exercice bien choisi vaut mieux qu’un long discours!
Exercice 1: Un bloc est tracté sur un plan horizontal par un bloc suspendu dans le vide
Enoncé: Deux blocs sont reliés par une corde sans masse. La surface horizontale est dépourvue de frottement (il peut s’agir d’un rail à coussin d’air par exemple). Si \(m_{1}=2kg\), quelle masse \(m_{2}\) faut-il suspendre pour donner au système une accélération de 5m/s²? Quelle sera alors la valeur de la tension dans la corde?
Reprenons les 3 étapes!
- Première étape: identification des forces agissant sur les deux masses.
- La force poids \(\overrightarrow {F_{G1}}\) dont la valeur est de 20 N.
- Le plan horizontal sur lequel \(m_{1}\) prend appui. Le plan réagit donc sur la masse de façon normale (ou perpendiculaire). Nous identifions la force de réaction normale, notée \(\overrightarrow {N}_{1}\) dont la valeur nous est à priori inconnue.
- La masse est également touchée par une corde tendue qui exerce logiquement une force de tension vers la droite notée \(\overrightarrow{T}\)
- La force poids \(\overrightarrow {F_{G2}}\) dont la valeur est inconnue: \(m_{2}.g\).
- Le plan horizontal ne touche pas \(m_{2}\) \(\Rightarrow\) il n’y a pas de force de réaction normale.
- La masse est uniquement touchée par la corde tendue qui exerce la même force de tension que sur \(m_{1}\) mais qui est orientée vers le haut cette fois. On la note évidemment \(\overrightarrow{T}\)
- Deuxième étape: Choix du référentiel. Dans notre cas, nous souhaitons une accélération de 5m/s² vers la droite. Le bloc \(m_{1}\) est donc en mouvement horizontal vers la droite. En toute logique, nous choisissons alors le référentiel X horizontal et orienté vers la droite pour \(m_{1}\) et vers le bas pour \(m_{2}\) puisque le seul effet de la poulie sera de dévier le mouvement.
- Troisième étape: Application du principe fondamental de la dynamique
- Conclusion: pour obtenir l’accélération recherchée (5m/s² vers la droite), il faut suspendre une masse de 2,1kg
-
\( \) Etude des forces agissant sur \(m_{1}\):
\( \) Dans ce cas, il n’y a pas de frottement (cfr énoncé), on se pose alors la question: qui touche la masse \(m_{1}\)?
\( \) Personne d’autre ne touche la masse \(m_{1}\), il n’y a donc aucune autre force!
ATTENTION
Il faut remarquer ici que la force de tension ne possède pas d’indice. Nous notons \(\overrightarrow{T}\) et non pas \(\overrightarrow{T}_{1}\). Pourquoi? Parce que la corde étant de masse négligeable, la tension qui règne en son sein est partout identique. Il ne faut donc absolument pas s’embarrasser d’indices 1 et 2 qui nous feraient croire à l’existence de deux inconnues dans les équations alors qu’il n’y en a qu’une, puisque la tension est partout la même dans la corde!
Etude des forces agissant sur \(m_{2}\):
Il n’y a bien entendu pas de frottement, on se pose donc la question suivante: qui touche la masse \(m_{2}\)?
\( \)
Nous obtenons la situation suivante:
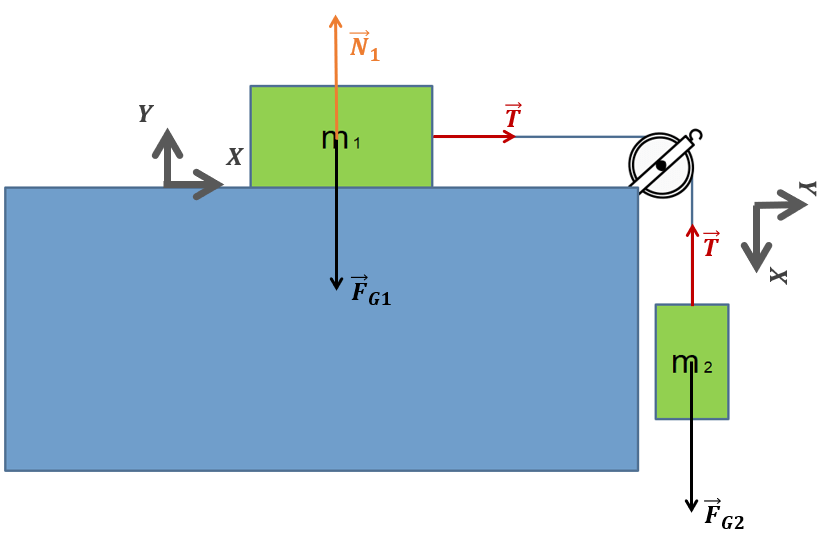
D’après la relation \(\Sigma \overrightarrow{F} = m.\overrightarrow{a}\), si on souhaite communiquer à chacune des deux masses une accélération de 5m/s², il faut qu’une force résultante agisse sur \(m_{1}\) vers la droite et qu’elle soit égale à \(\Sigma F_{1}=m_{1}.5\). En effet, si l’accélération se fait vers la droite, elle possède une composante scalaire positive (+5) dans notre référentiel X. De même, étant donné que la corde reste tendue, il faut que la masse \(m_{2}\) subisse une accélération de 5m/s² vers le bas (et donc: \(a=+5\) dans notre référentiel X). Il faut donc qu’une force résultante de valeur \(\Sigma F_{2}=m_{2}.5\) agisse sur \(m_{2}\) . \( \)
Application du PFD sur \(m_{1}\)
\( \)
Observons le schéma de la Fig.2. En nous approchant de \(m_{1}\) le long de l’axe X et en venant de \(-\infty\), quelles forces rencontre-t-on? La seule et unique force qui possède la même direction que X est la force de tension \(\overrightarrow{T}\) qui est orientée dans le sens du référentiel et qui possède donc une composante scalaire positive: +T. C’est la seule force, elle joue à elle seule le rôle de force résultante \(\Sigma F_{1}\). Etant donné que la valeur de la masse est 2 kg, nous obtenons :
\begin{align} \Sigma F_{1}=m_{1}.a \Leftrightarrow +T = 2.5 = 10 \end{align}
On trouve dans ce cas, tout de suite la valeur de la tension dans (toute) la corde.
\( \)
Application du PFD sur \(m_{2}\)
\( \)
De façon similaire, sur la Fig.2, en nous approchant de \(m_{2}\) le long de l’axe X et en venant de \(-\infty\), quelles forces rencontre-t-on? On rencontre d’abord la force de tension \(\overrightarrow{T}\) qui est orientée dans le sens opposé au référentiel X et qui possède donc une composante scalaire négative: -T. On rencontre également la force poids \(\overrightarrow{F}_{G2}\), qui est orientée dans le sens du référentiel et qui possède donc une composante scalaire positive: \(+F_{G2}=m_{2}.9,81\). Pour cette seconde masse, il y a donc deux forces qui s’additionnent pour donner la force résultante \(\Sigma F_{2}\). Nous obtenons :
\begin{align} \Sigma F_{2}=m_{2}.a \Leftrightarrow -T + m_{2}.9,81 = m_{2}.5 \end{align}
L’équation (1) nous a donné la valeur de la tension dans la corde, nous pouvons réécrire la relation (2):
\begin{equation} \left\lbrace \begin{aligned} -10 + m_{2}.9,81 &= m_{2}.5 4,81.m_{2} &= 10 m_{2} &=\frac{10}{4,81} = 2,1 \end{aligned} \right. \end{equation}
Exercice 2: Bloc poussé sur un plan incliné
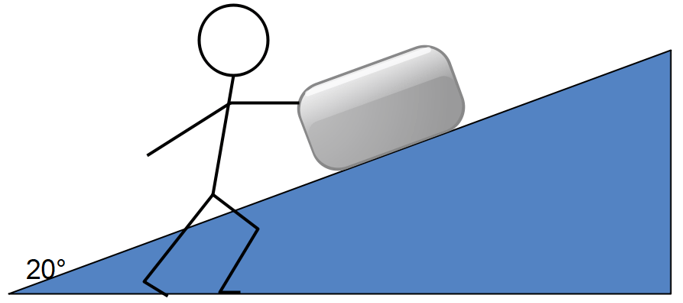
Enoncé: Un bloc de 3kg est placé sur un plan incliné à 20° sans frottement. Une personne de 50kg exerce une force horizontale de 10N sur ce bloc. Est-ce suffisant pour que le bloc glisse vers le haut? Quelle sera son accélération?
\( \) Reprenons une fois encore les 3 étapes! Remarquons cette fois que l’énoncé nous donne la masse du personnage alors que c’est l’accélération du bloc qui est demandée. Ne vous laissez pas influencer par des données parasites! On fait l’étude des forces sur la masse, c’est elle seule qui nous intéresse!
- Première étape: identification des forces agissant sur la masse.
- La force poids \(\overrightarrow {F_{G}}\) dont la valeur est de 30 N.
- Le plan horizontal sur lequel \(m\) prend appui. Le plan réagit donc sur la masse de façon normale (ou perpendiculaire). Nous identifions la force de réaction normale, notée \(\overrightarrow {N}\) dont la valeur nous est à priori inconnue.
- La masse est également touchée par le personnage qui exerce une force musculaire horizontale notée \(\overrightarrow{F}\)
- Deuxième étape: Choix du référentiel. Dans notre cas, nous souhaitons étudier le mouvement (et donc l’accélération) du bloc. Ce bloc ne peut que glisser le long du plan incliné vers le haut ou vers la bas, ça nous ne le savons pas! Supposons donc que le mouvement se fait vers le haut, nous choisissons alors un référentiel X le long du plan et orienté vers son sommet.
- Troisième étape: Application du principe fondamental de la dynamique
- Conclusion: Quelle est la signification physique de ce résultat? Malgré la force appliquée par le personnage, la force résultante est orientée vers le bas (à l’opposé du référentiel X choisi). Elle donne donc lieu à une accélération orientée vers le bas. La force musculaire appliquée est donc insuffisante pour pousser le bloc vers le haut. Il glissera vers le bas avec une accélération de 0,3m/s².
\( \)
\( \) Dans ce cas, il n’y a pas de frottement (cfr énoncé), on se pose alors la question: qui touche la masse \(m\)?
\( \) Personne d’autre ne touche la masse \(m\), il n’y a donc aucune autre force!
\( \)
Nous obtenons la situation suivante:
\( \) 
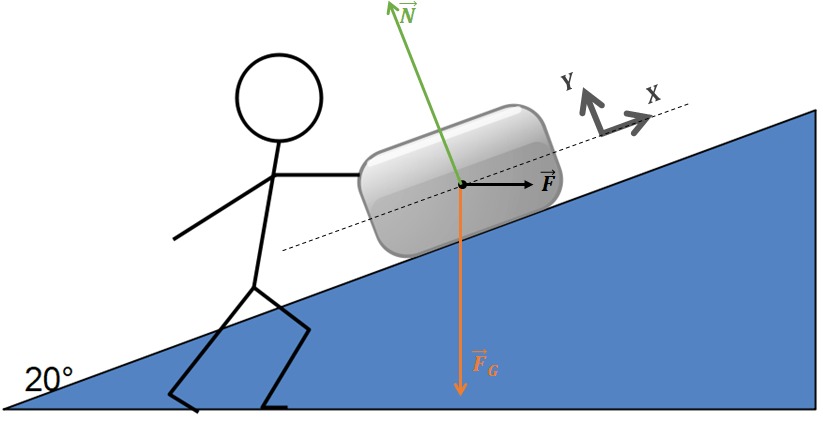
Dans la relation \(\Sigma \overrightarrow{F} = m.\overrightarrow{a}\), nous ne connaissons pas l’accélération \(\overrightarrow{a}\) cette fois, mais l’ensemble des forces appliquées desquelles il nous faut déduire la force résultante \(\Sigma \overrightarrow{F}\). Nous observons sur la Fig.5 que les forces \(\overrightarrow{F}\) et \(\overrightarrow{F}_{G}\) n’agissent pas le long du référentiel (X,Y), mais entre ces deux directions. Il nous faut dès lors décomposer les deux forces, ce qui nous conduit à la Fig.6.
\( \) 
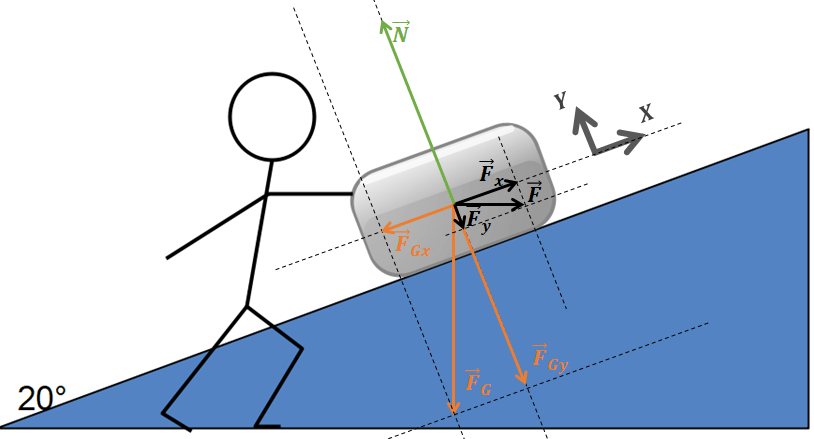
ATTENTION: Cette étape doit être réalisée soigneusement pour faciliter le travail par la suite. Les composantes vectorielles orientées le long du référentiel X porteront le nom de la force dont elles sont issues auquel on ajoutera un indice x. Ainsi, la composante de la force \(\overrightarrow{F}\) orientée le long de X sera notée \(\overrightarrow{F}_{x}\) tandis que celle qui est orientée le long de l’axe Y sera notée \(\overrightarrow{F}_{y}\). C’est un détail mais qui fera probablement toute la différence par la suite!
\( \)
Une bonne habitude consiste également à directement exprimer ces composantes en fonction de leur force d’origine à l’aide de la trigonométrie. Il suffit d’appliquer les relations sinus et cosinus dans les triangles orange et noir de la Fig.7. Pas de panique! Ce n’est pas compliqué, si vous remarquez que l’angle de 20° s’y retrouve (côtés perpendiculaires deux à deux pour le triangle orange avec les côtés du plan incliné et angles correspondants dans le triangle noir).
\( \) 
Nous obtenons donc:
\( \)
Dans le triangle orange:
\( \)
\begin{align} sin(20°)=\frac{F_{Gx}}{F_{G}} \, \Leftrightarrow \, F_{Gx}=F_{G}.sin(20°)=30.sin(20°)=10,3 \end{align} \begin{align} cos(20°)=\frac{F_{Gy}}{F_{G}} \, \Leftrightarrow \, F_{Gy}=F_{G}.cos(20°)=30.cos(20°)=28,2 \end{align}
\( \)
Dans le triangle noir:
\( \)
\begin{align} sin(20°)=\frac{F_{y}}{F} \, \Leftrightarrow \, F_{y}=F.sin(20°)=10.sin(20°)=3,4 \end{align} \begin{align} cos(20°)=\frac{F_{x}}{F} \, \Leftrightarrow \, F_{x}=F.cos(20°)=10.cos(20°)=9,4 \end{align}
\( \)
Application du PFD sur \(m\)
\( \)
Observons le schéma de la Fig.6 ou 7: en nous approchant de \(m\) le long de l’axe X et en venant de \(-\infty\), quelles forces rencontre-t-on? Nous rencontrons tout d’abord la force \(\overrightarrow{F}_{Gx}\) qui agit dans le sens opposé au référentiel X choisi, elle possède donc une composante scalaire négative notée \(-F_{Gx}\). Viens ensuite la composante x de la force musculaire \(\overrightarrow{F}_x\) qui agit dans le sens du référentiel et qui possède donc une composante scalaire positive notée \(+F_{x}\). La force résultante le long de l’axe x est donc la somme de ces deux composantes scalaires et nous obtenons:
\begin{align} \Sigma F_{x}=m.a_{x} \Leftrightarrow -F_{Gx} + F_{x} = 3.a_{x} \end{align}
Or, les relations (4) et (7) nous donnent les valeurs de \(F_{Gx}\) et \(F_{x}\). Nous pouvons donc réécrire la relation (8):
\begin{align} -10,3 + 9,4 = 3.a_{x} \Leftrightarrow -0,9 = 3.a_{x} \Leftrightarrow a_{x} = -0,3 \end{align}
On observe que la composante scalaire de la force résultante le long du plan incliné est négative: \(\Sigma F_{x}=-0,9 N\), elle conduit évidemment à une accélération de composante scalaire négative: \(a_{x}=-0,3 m/s²\).
\( \)
\( \)
Remarque: dans cet exercice, les relations (5) et (6) ne nous ont pas été utiles parce qu’il n’y a pas de force de frottement. Sachez toutefois qu’elles interviendront dans les exercices avec frottement. Si vous êtes prêts à les affronter, je vous donne rendez-vous sur cette page! Bon courage et à bientôt!
\( \)
Si cette page vous a aidé(e) à progresser dans la compréhension de votre cours de physique, ce serait vraiment sympa de me laisser un petit commentaire ou même simplement un like, que je sache si mon travail est utile ou si je pédale dans le vide! 😉 Merci!
Partager l'article:
administrator
10 commentaires pour l’instant
ElisePublié le6:33 pm - Fév 27, 2019
J’ai beaucoup aimé l’astuce d’enlever les indices pour le tension. Effectivement c’est beaucoup plus pratique pour résoudre l’exercice et on risque moins de s’y perdre.
yelPublié le4:34 pm - Juin 14, 2021
Bonjour, pourrais je avoir le correctif des exercices svp,?
merci d’avance :))
Gordon FreemanPublié le5:59 pm - Oct 13, 2021
Magnifique j’ai compris des mois de cours en un petit site grandiose <3
Merci beaucoup pour votre aide !
Julie ColauxPublié le9:09 am - Oct 14, 2021
Et merci à vous d’avoir pris le temps de me faire ce retour positif!
Belle journée et bon courage pour la suite!
AlbertPublié le7:34 pm - Août 17, 2022
Je trouve que la présentation et les exemples donnés ne sont pas assez ludiques ni pédagogiques. Il faut revoir le visuel des schémas proposés qui sont beaucoup trop pauvres et donnent une impression technique, donc ennuyante, et il faut revoir entièrement la présentation descriptive des problèmes qui semble ne jamais finir à force de dérouler la page sans cesse…. Aussi il n’y a aucune explication sur sinus et cosinus il aurait fallut faire un rappel sur la page même dans un encadré… bref c’est un travail basique d’enseignant de la fonction publique qui donne toujours ce même goût fade aux sciences à force de les présenter avec si peu d’intelligence.
Julie ColauxPublié le3:49 pm - Août 18, 2022
Bonjour Monsieur,
Merci pour votre commentaire. J’imagine avoir la chance d’être face à un professionnel avec de belles compétences en physique, mais aussi en pédagogie et en graphisme ? Quel est votre métier ? Comme j’ai toujours la volonté de m’améliorer, je vous propose de me donner en exemple votre travail ; peut-être avez-vous déjà un site avec des exemples plus ludiques que les miens ? Pourriez-vous m’en donner la référence, que je puisse m’inspirer de votre travail ? Si pas, accepteriez-vous de m’écrire un article sur le même sujet que celui-ci mais dans lequel la matière scientifique serait présentée avec plus d’intelligence ? Je pourrais le publier sur mon blog en indiquant clairement que vous en êtes l’auteur, bien évidemment.
En attendant de vous lire,
Julie Colaux
AOPublié le5:33 pm - Jan 14, 2023
Alors le commentaire de « Albert » ; quelle suffisance, quelle prétention, quel mépris pour le travail d’autrui !
Je serais bien contente de connaitre des sites qui remplissent les critères qu’il mentionne et surtout de voir son travail publié et mis ainsi à disposition de tous.
Et je suis aussi bien contente de ne pas l’avoir eu comme professeur ou comme collègue.
Mme Colaux, bravo pour votre travail.
Justement, j’adore donner les références de votre site à mes élèves car ils y trouvent les explications détaillées et plein de schémas bien faits et sans aucune approximation ou erreur mathématique pour des questions de physique qui mobilisent des compétences en mathématiques de plusieurs chapitres.
C’est une matière vue pour la première fois par des élèves en 5e secondaire (en Belgique) et qui mélange 2-3 chapitres différents de mathématique de 4e secondaire.
Ce sont des exercices complexes à maitriser .
Je ne trouve pas qu’il faut rendre les sciences « amusantes » à la mode « C’est pas sorcier ». Il faut les rendre compréhensibles et c’est ce que votre blog fait à merveille en détaillant pas à pas les étapes.
Ce sont des questions qui interviennent régulièrement dans les qcm de notre cher examen d’entrée de médecine … présenté par de nombreux étudiants français …
Merci . Et surtout continuez ainsi.
A .O.
Julie ColauxPublié le12:11 pm - Jan 15, 2023
Bonjour Madame et merci pour votre commentaire!
J’ai arrêté l’échange avec Albert, après son second retour (que j’ai décidé de ne pas publier), plus âpre encore que le premier.
A ce jour, je n’ai toujours reçu aucune référence de son travail; juste des critiques du mien.
Je suis sur la même longueur d’onde que vous. Pour moi, donner le goût des sciences aux jeunes, c’est leur apprendre à ne pas en avoir peur, tout en gardant le niveau de rigueur que la physique exige.
Je vous souhaite une belle journée et une bonne fin d’année scolaire!
Julie
À propos de l’auteur