Recevez gratuitement
mon livret!
Propagation des ondes
Enoncé du principe de Huygens : Lorsqu’une onde se propage, chaque élément de surface atteint par cette onde, se comporte comme une source secondaire qui émet des ondelettes sphériques appelées ondelettes d’Huygens. L’œil ne distingue pas ces ondelettes mais uniquement leur enveloppe. Le front de l’onde à un instant t+dt se déduit du front de cette onde à l’instant t, en considérant que l’enveloppe des ondes secondaires d’Huygens s’est propagée pendant l’intervalle de temps dt, comme le montre la Fig.1.
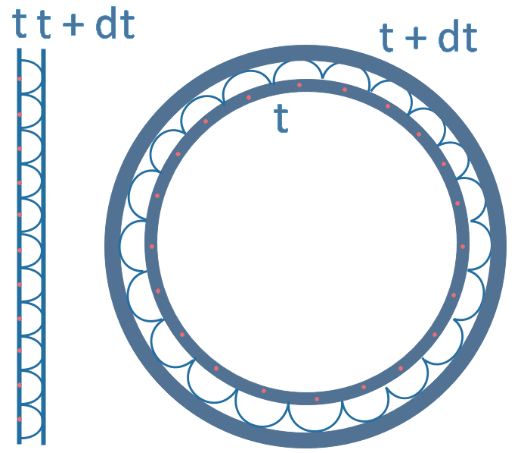
Huygens permet dès lors d’expliquer qu’une onde plane se propage de proche en proche en restant plane alors qu’une onde sphérique reste sphérique.
Passage des ondes à proximité d’un obstacle
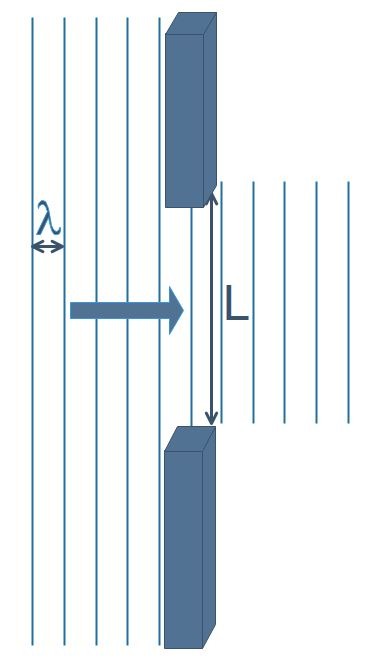
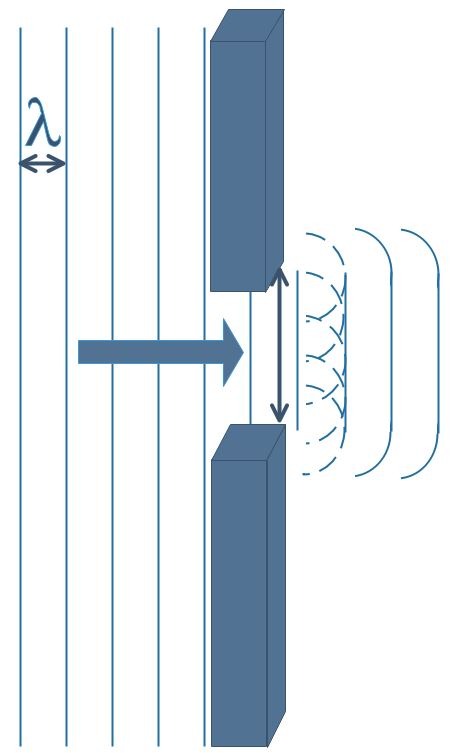
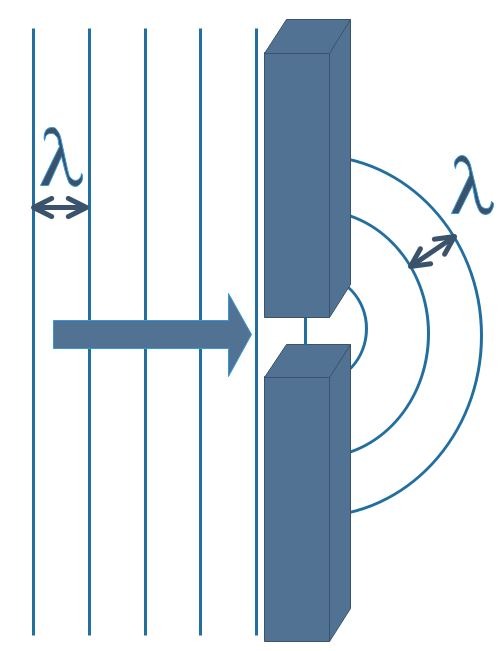
Lorsqu’une onde rencontre un obstacle ou passe au travers d’une ouverture de dimension L, elle peut subir une diffraction. Il est possible d’observer ce phénomène dans une cuve à ondes. La propagation rectiligne des ondes est plus ou moins modifiée en fonction de la valeur relative de la longueur d’onde par rapport à l’obstacle.
- Si \(\lambda <<< L \): La partie du front de l’onde qui touche l’obstacle est réfléchie vers l’arrière, tandis que le reste du front de l’onde poursuit son chemin au travers de l’ouverture de largeur L comme le représente le schéma de la Fig.2.
- Au fur et à mesure que la dimension de l’ouverture diminue par rapport à la longueur d’onde, les ondes se diffractent en traversant l’ouverture comme le montre la Fig.3. On a représenté les ondelettes de Huygens sur le premier front qui franchit l’ouverture.
- Lorsque la dimension de l’ouverture devient comparable à la longueur d’onde, les fronts d’onde sont à ce point diffractés qu’ils deviennent sphériques comme le montre la Fig.4.
\(\\\)
\(\\\)
\(\\\)
Diffraction de la lumière à travers une fente
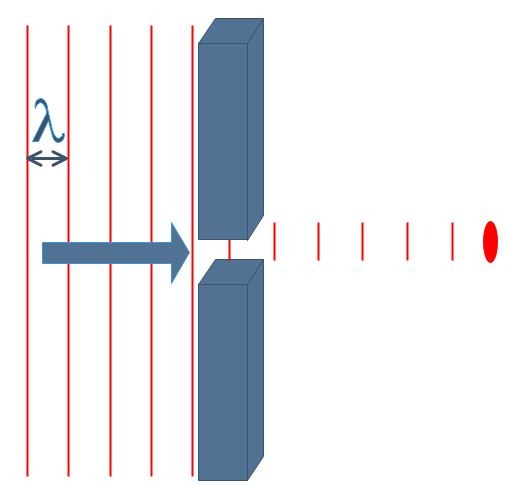
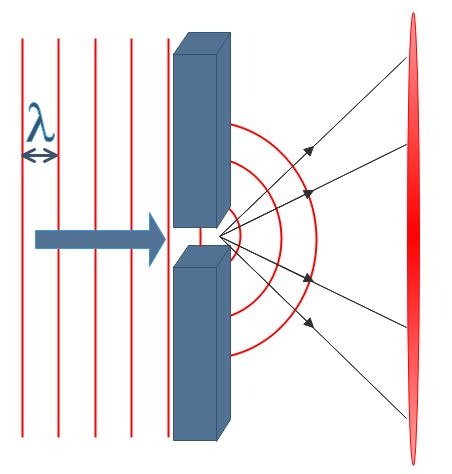
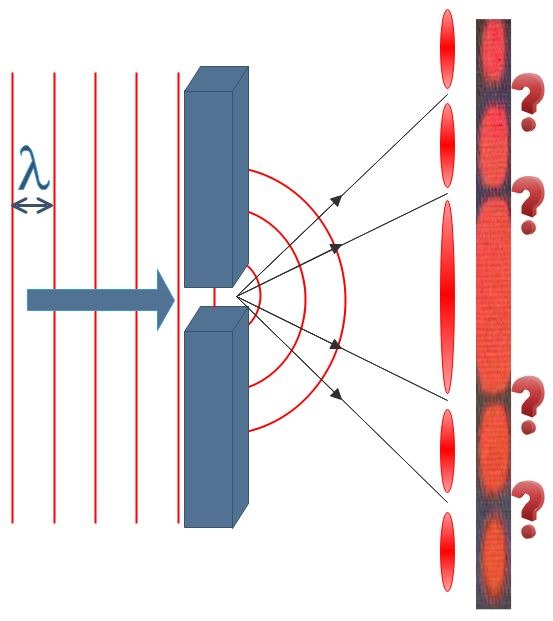
Nous venons d’étudier le comportement des ondes mécaniques à la surface de l’eau, mais un phénomène similaire se produit avec la lumière. En effet, lorsqu’un expérimentateur tente de réduire un faisceau laser à un pinceau le plus mince possible en guidant le spot laser à travers une fente de très petite dimension, c’est l’inverse qui se produit ! Au lieu de former un pinceau tout mince (Fig.5), la lumière subit une diffraction et s’étale de part et d’autre de l’ouverture. Le principe de Huygens et la Fig.4 nous permettent de comprendre ce phénomène modélisé à la Fig.6. Toutefois, en regardant plus attentivement la figure de diffraction projetée sur le mur, on aperçoit des régions obscures dans lesquelles la lumière diffractée s’éteint en plusieurs endroits (Fig.7) … et ça, Huygens ne nous l’explique pas!
\(\\\)
Comment interpréter l’existence de zones sombres dans la figure de diffraction?
Les conditions de Fraunhofer
Remarquons tout d’abord que nous sommes dans les conditions de diffraction de Fraunhofer: la source est éloignée de la fente qui est elle-même éloignée du mur sur lequel nous faisons nos observations comme le montre la Fig.8.
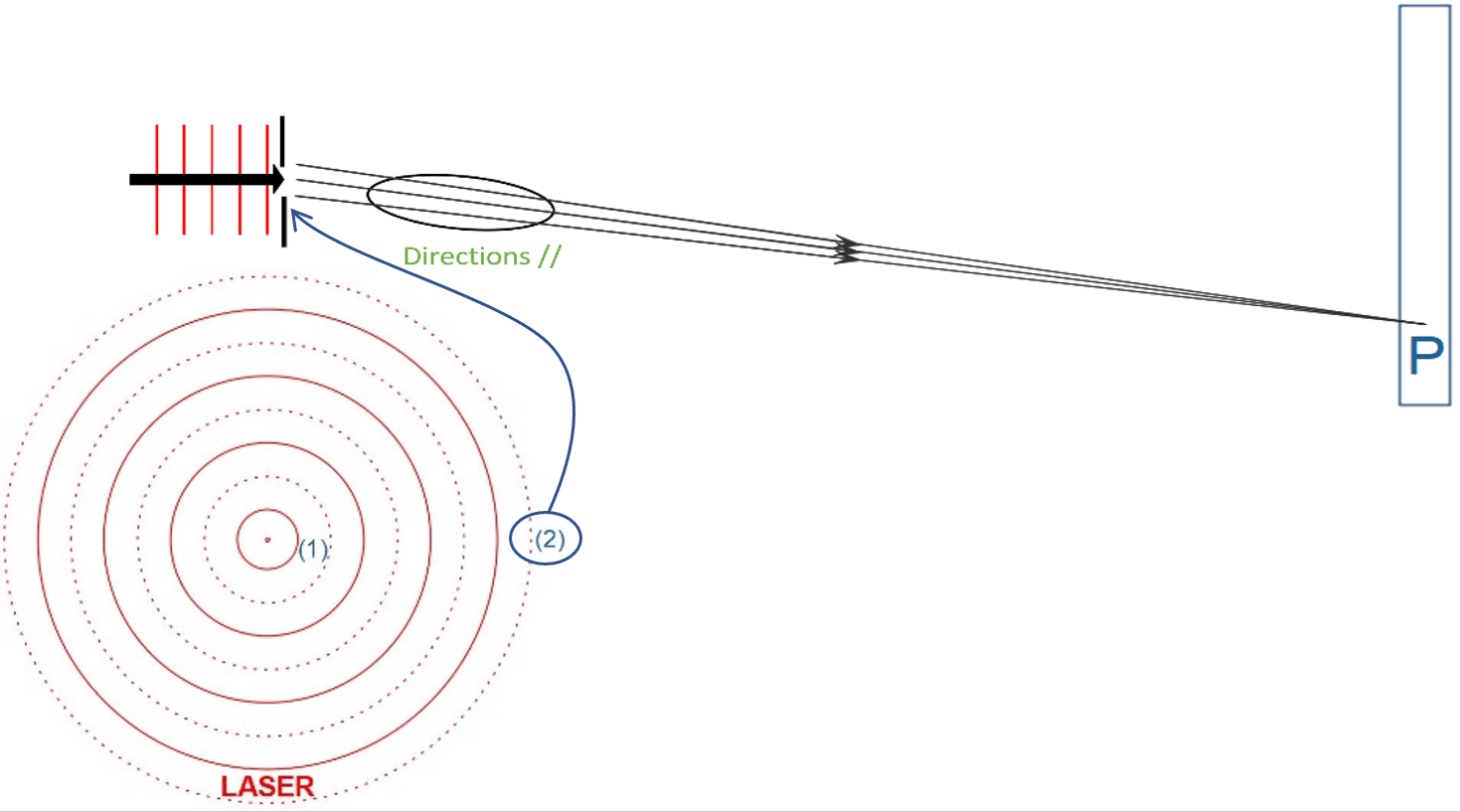
Qu’est-ce que cela change, ces conditions de Fraunhofer? Et bien, deux choses:
- La source laser émet des ondes circulaires. Si l’ouverture était placée tout près de la source (position (1) de la Fig.8), les fronts de l’onde auraient une courbure forte que l’on ne pourrait pas négliger. En se plaçant à plus grande distance de la source laser, l’ouverture étant de petite dimension et les fronts de grand rayon de courbure, on peut sans problème faire l’approximation suivante: une onde plane traverse l’ouverture.
- Le mur sur lequel les observations seront faites (au point P par exemple) étant situé à une grande distance de l’ouverture, si on trace la direction de propagation des ondelettes de Huygens émises à partir de cette ouverture en direction d’un point donné (P), on s’aperçoit qu’elles sont quasiment parallèles entre elles. Il faut bien comprendre que l’ouverture est de très petite dimension (une fraction de mm) tandis que le mur est situé à plusieurs mètres de la source laser. Il me semble que cela vaut la peine, à ce stade, de s’imaginer ce que la Fig.8 donnerait « grandeur nature ».
Pourquoi le point situé le long de la médiatrice de l’ouverture est-il un point lumineux?
Maintenant que les conditions sont posées, réalisons un zoom sur l’ouverture. Selon le principe de Huygens, on peut considérer que le front plan qui traverse cette ouverture (de largeur L) se comporte comme une suite de sources secondaires qui émettent des ondelettes dans toutes les directions. Pour ne pas surcharger le dessin, la Fig.9 représente seulement 14 sources secondaires. Parmi ces sources, nous avons uniquement modélisé l’émission des sources 1, 7 et 14. En réalité, chaque source secondaire émet des ondelettes dans toutes les directions.
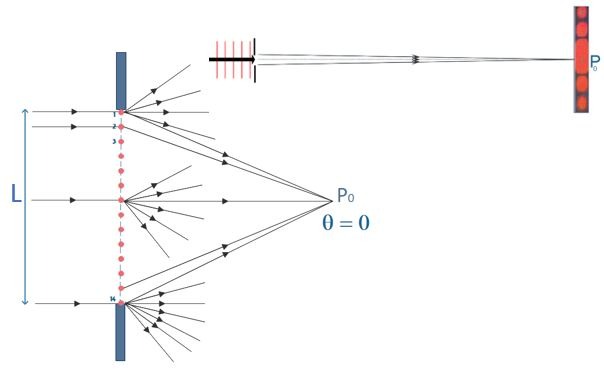
Plaçons notre œil au point \(P_{0}\) situé dans une direction \(\theta = 0°\) par rapport à la médiatrice de l’ouverture. Seules les ondes émises dans cette direction par chacune des 14 sources secondaires nous parviennent. On remarque, sur la Fig.9, que les rayons 1 et 14 interfèrent de façon constructive au point \(P_{0}\) puisqu’ils parcourent exactement la même distance. Il en est de même pour les rayons 2 et 13, mais aussi pour les rayons 3 et 12, 4 et 11 … Nous observerons donc une zone de lumière intense au point \(P_{0}\). On appellera ce point le maximum central de diffraction.
\(\\\)
Pourquoi le point situé à un angle \(\theta_{1}\) de la médiatrice est-il un point sombre?
Pour tout point P positionné dans une autre direction (\(\theta \neq 0°\)), la situation n’est plus symétrique et légèrement plus compliquée.
La Fig.10 retrace la situation pour laquelle la direction d’observation \(\theta_{1}\) est telle que les ondelettes émises par les sources secondaires 1 et 7 interfèrent destructivement. On voit en effet que, dans cette direction, l’onde 7 doit parcourir une demi-longueur d’onde en moins que l’onde 1. Dès lors, ces deux ondes arrivent au point \(P_{1}\) en opposition de phase et y interfèrent de façon destructive. On pourra faire un raisonnement similaire entres les ondes 2 et 8, 3 et 9 … Au final, le point \(P_{1}\) situé dans cette direction \(\theta_{1}\) recevra des ondes qui se détruisent deux à deux et correspondra à un endroit où il n’y a pas de lumière. On appellera ce point le minimum de diffraction d’ordre 1.
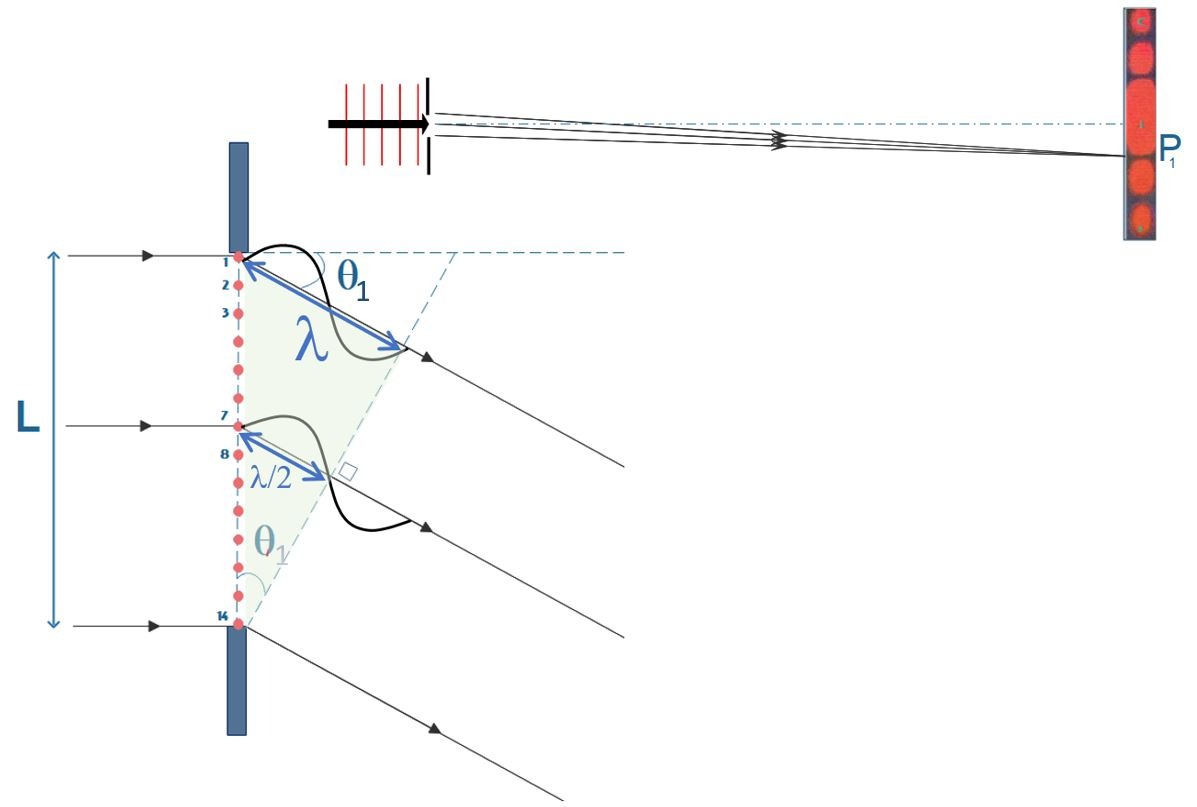
En observant le triangle coloré de la Fig.10, on peut écrire la relation suivante :
\begin{equation}
\sin(\theta_{1})=\frac{\lambda}{L}
\tag{1}
\end{equation}
Ce premier angle \(\theta_{1}\) nous donne donc la direction dans laquelle nous observons la première zone sombre à partir du maximum central de diffraction.
\(\\\)
Pourquoi le point situé à un angle \(\theta_{2}\) de la médiatrice est-il un point sombre?
Si on augmente progressivement l’angle \(\theta\), le point \(P\) se déplace le long du mur jusqu’à atteindre une deuxième zone d’ombre: il s’agit du point \(P_{2}\) de la Fig.11.
Imaginons maintenant que nous divisions la fente comme sur la Fig.11.
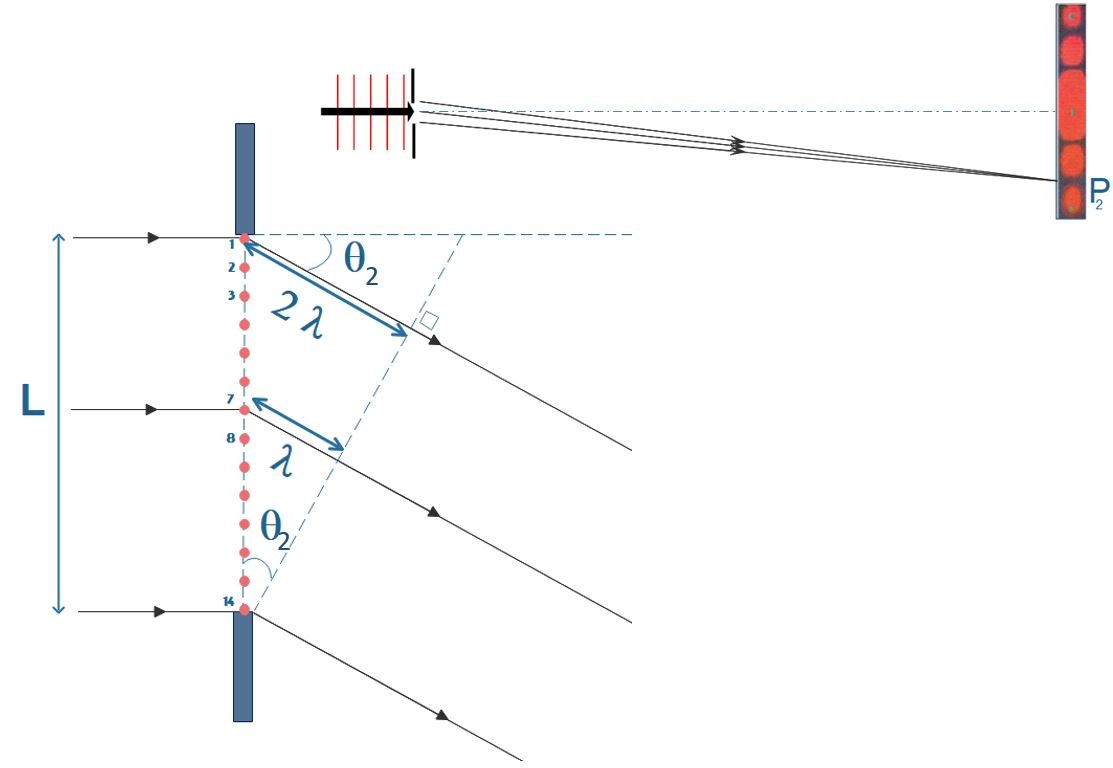
Dans cette figure, on remarque que le triangle compris entre les ondelettes 7 et 14 correspond exactement à la situation décrite à la Fig.10. Par transposition, on pourra facilement imaginer que la partie supérieure de la fente (comprise entre les ondelettes 7 et 1) se comportera de la même façon également. On retrouvera donc un deuxième minimum de diffraction dans cette direction et un peu de géométrie nous permettra d’écrire:
\begin{equation}
\sin(\theta_{2})=2\frac{\lambda}{L}
\tag{2}
\end{equation}
Pourquoi le point situé à un angle \(\theta_{3}\) de la médiatrice est-il un point sombre?
On peut continuer le raisonnement et augmenter encore l’angle d’observation de façon telle que la différence de marche entre les sources 1 et 14 soit de 3 longueurs d’onde. On peut alors couper la fente en 3 parties identiques et reprendre un raisonnement similaire à ce qui précède: si on coupe chacune des trois parties en deux sous-parties, les ondelettes de chacune de ces sous-parties interfèrent destructivement deux à deux. Cela nous conduira à la relation suivante pour la troisième extinction:
\begin{equation}
\sin(\theta_{3})=3\frac{\lambda}{L}
\tag{3}
\end{equation}
On généralisera ces résultats (équations (1) à (3)) en écrivant qu’il y a interférence destructive complète et donc existence de minima de diffraction (ou encore de zones sombres) dans les directions \(\theta_{k}\) telles que :
\begin{equation}
\sin(\theta_{k})=k\frac{\lambda}{L} \; avec \; k = \pm 1 \, ; \pm 2 \, ; \pm 3 \, …
\end{equation}
Attention ! La valeur k = 0 est à rejeter puisque dans la direction \(\theta = 0°\), il y a des interférences constructives et donc un maximum lumineux.
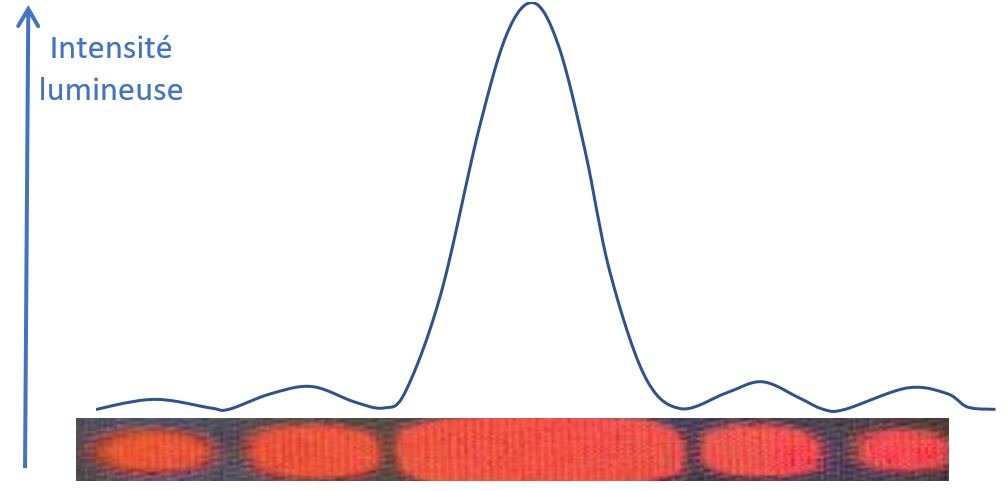
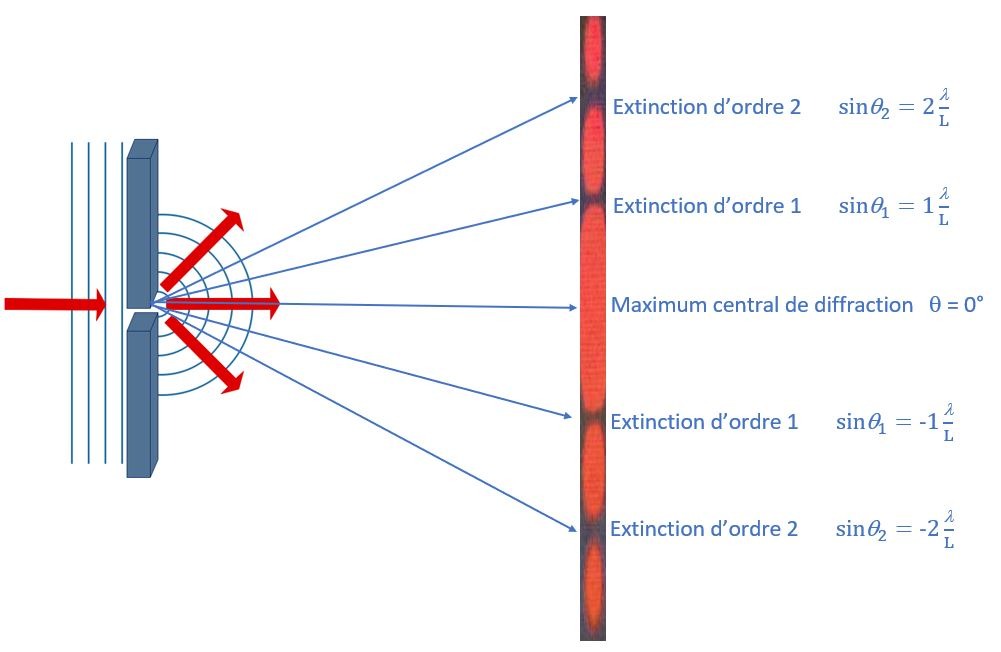
Remarquons enfin que, en se déplaçant progressivement depuis le maximum central de diffraction vers l’extinction de 1er ordre (càd en se déplaçant de \(P_{0}\) vers \(P_{1}\)), la lumière s’éteint progressivement puisque les ondes parviennent de plus en plus déphasées les unes par rapport aux autres. On peut donc tracer le profil en intensité lumineuse de la Fig.12.
Synthèse
Lorsqu’on essaie de réduire un spot laser (monochromatique) à un faisceau très étroit, plus la fente diminue et plus la lumière nous joue un pied de nez en étalant le spot laser par diffraction. En observant le spot large produit par la fente mince, on remarque une succession de points sombres sur lesquels les différents rayons lumineux issus de la fente interfèrent destructivement. La relation suivante nous donne les directions \(\theta_{k}\) des extinctions lumineuses:
\begin{equation}
\sin(\theta_{k})=k\frac{\lambda}{L} \; avec \; k = \pm 1 \, ; \pm 2 \, ; \pm 3 \, …
\end{equation}
L’intensité lumineuse est maximale le long de la médiatrice et décroissante au fur et à mesure qu’un minimum de diffraction (càd qu’une extinction) est approché.
La figure 13 reprend toutes ces notions.
J’espère que cet article vous a plu ou qu’au minimum il vous a été utile. Si c’est le cas, n’hésitez pas à le liker 😉
Si vous préférez apprendre à partir d’une vidéo, ce lien pourra vous être utile: Vidéo
Il pourrait également être intéressant de faire des exercices
Partager l'article:
administrator
6 commentaires pour l’instant
DianePublié le10:47 pm - Mar 1, 2019
Merci c’est tellement bien expliqué que moi-même j’ai compris. LOL , oui parce que ce n’est pas mon domaine mais qu’il m’intéresse tout de même. En fait j’aime savoir comment se comporte notre univers. C’est par des observations, réflexions et finalement des théories mises à l’épreuve par de grands génies (ou des gens tenaces) que nous découvrons ensemble notre monde.
Michel DelmasPublié le9:56 pm - Oct 12, 2022
Cet article est à la limite d’un cours et de la vulgarisation scientifique de très bon niveau, sans simplification abusives ou schémas douteux . Merci beaucoup !
dominiquePublié le1:24 pm - Jan 11, 2023
cet article m’a permis d’éclairer les explications de mon cours. Merci à vous c’est très clair et instructif
Julie ColauxPublié le2:59 pm - Jan 11, 2023
Et merci à vous d’avoir pris le temps de me faire ce retour positif!
À propos de l’auteur