L’équation d’onde sinusoïdale progressive

Comment exprimer mathématiquement le déplacement le long d’un référentiel X d’une onde sinusoïdale, ou encore, comment démontrer l’équation d’onde sinusoïdale progressive? C’est l’objet de cet article. Après le rappel d’un outil mathématique essentiel à comprendre, nous nous lancerons dans la (petite) démonstration de l’équation d’onde progressive.

Pourquoi est-ce important d’étudier l’équation d’onde sinusoïdale progressive?

Parce que la maitrise de cette équation vous conduira tout droit vers la compréhension des modes stationnaires qui expliquent, entre autres, la beauté de la physique à l’œuvre dans des instruments de musique.

Que faut-il comprendre avant de se lancer dans la démonstration?

Deux petites choses: une en math, l’autre en physique. Honneur aux mathématiques…

La translation des fonctions le long de l’axe des abscisses.

Imaginez une fonction mathématique pas trop compliquée: \(y(x)=2x^{2}\) dont voici le graphe.
\(\\\)

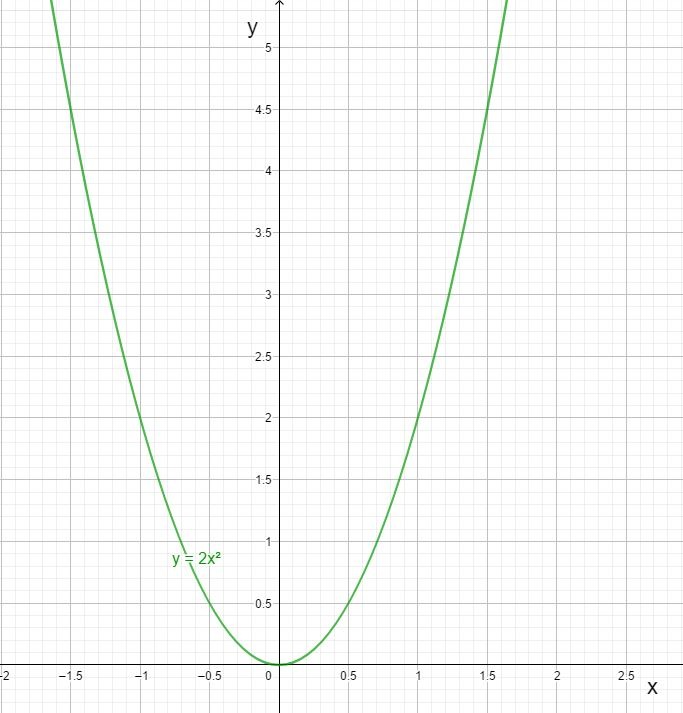
Le zéro de cette fonction est zéro, en effet: \(y(0)=0\).
Translatez maintenant ce graphique, disons de +1 unité vers la droite. Voici le graphe que vous obtenez: \(\\\)

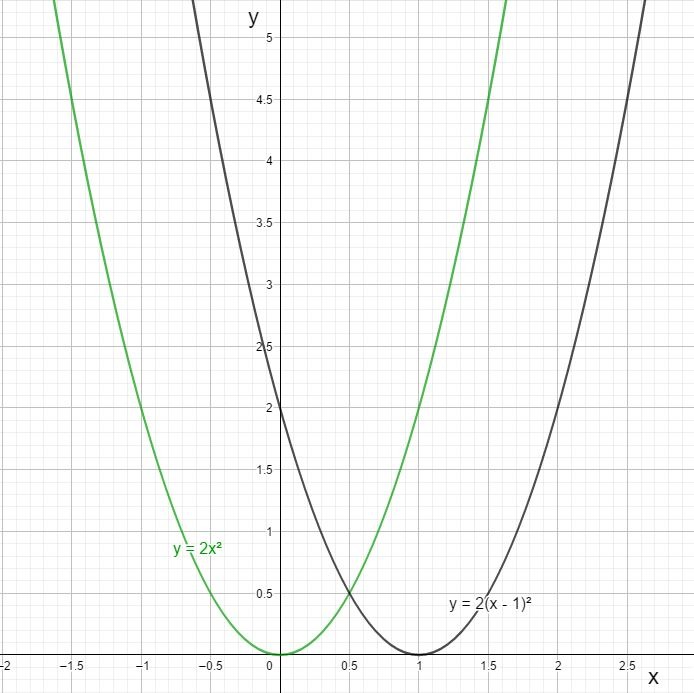
Le zéro n’est plus zéro, mais bien 1. La fonction \(y(x) = 2x^{2}\), devient: \(y(x) = 2(x-1)^2\). En effet, quand vous remplacez x par 1 \(\Rightarrow\) y vaut 0! Et ceci fonctionne pour n’importe quelle fonction!

Vous retenez donc ceci: si je veux faire glisser une fonction de +1 unité le long des abscisses, j’affecte l’abscisse de \( \ \) -1 \( \; \Rightarrow \;\) \(x \ \) devient \( \ (x-1)\)

Le déplacement de l’onde sinusoïdale

Dans la démonstration qui suit, vous allez considérer une onde sinusoïdale qui se propage vers la droite dans une corde. Si les propriétés de la corde sont en tous points identiques, alors, l’onde se propage dans cette corde à vitesse constante. Concentrez-vous sur « la tête » de l’onde, vous allez voir un point qui avance en ligne droite à vitesse constante, exactement comme un mobile en MRU! Aaaahhhh, ce bon vieux MRU! Comme vous avez été drillé quand on a étudié le MRU ensemble, vous savez que:

Qui dit MRU, dit
\begin{equation}
\Delta x = v. \Delta t \\
\end{equation}
Eh bien, retenez ça aussi!

Enfin, par définition, la longueur d’onde (\(\lambda\)) est la distance que parcourt l’onde en une période (\(T\)). La période étant le temps nécessaire pour que la source ou n’importe quel point atteint par l’onde effectue un mouvement vertical d’aller-retour complet (\(0 \Rightarrow +A \Rightarrow 0 \Rightarrow -A \Rightarrow 0\)). Vous retiendrez donc enfin que:

\begin{equation}
\lambda = v. T \\
\end{equation}

La démonstration est-elle compliquée?

Absolument pas! Suspendez le temps (en prenant une photo) et observez une onde qui se propage dans une corde, comme ceci:

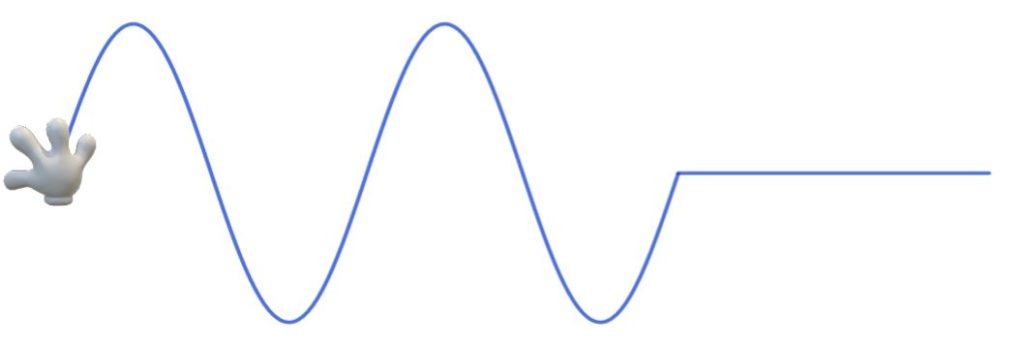
Si vous voulez étudier ce mouvement de l’onde, vous devez poser un référentiel. Or, l’onde avance en soulevant la corde transversalement, il nous faut donc étudier deux directions: la direction de propagation \(\Rightarrow\) X et la direction de déformation \(\Rightarrow\) Y.
\(\\\)

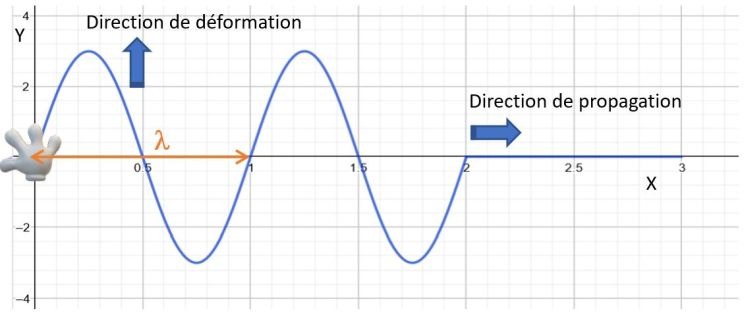
Comme vous gérez en math, vous reconnaissez de suite la fonction:
\begin{equation}
y(x)=A.sin(\frac{2 \pi}{\lambda}.x) \\
\end{equation}

Petite vérification: quand je remplace \(x\) par \(\frac{\lambda}{2}\), j’obtiens: \(y(\frac{\lambda}{2})=A.sin(\frac{2 \pi}{\lambda}.\frac{\lambda}{2})=A sin(\pi)\)=0. OK!
\(\\\)
Bon, vous avez suspendu le temps assez longtemps! Relancez la machine et contentez-vous de prendre une photo tous les quarts de période (\(\frac{T}{4}\)). Rappelez-vous que, par définition (2), l’onde avance d’une longueur d’onde en une période. Elle avance donc d’un quart de longueur d’onde en un quart de période. Voilà ce que vous devriez obtenir: \(\\\)

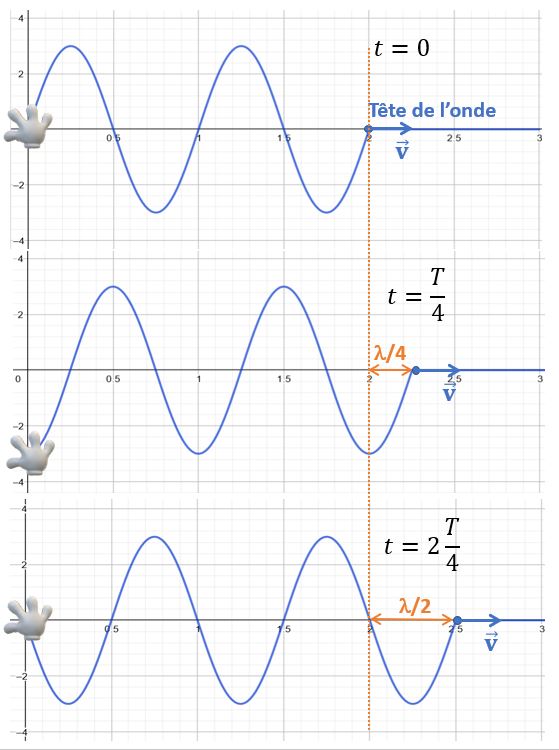
Si vous avez retenu le rappel de physique, vous ne me contredirez pas si je vous dis que pendant un temps \(t\), la tête de l’onde avance à vitesse constante d’une distance \(\Delta x = vt\). Ah, et donc, c’est juste la fonction \(y(x)=A.sin(\frac{2 \pi}{\lambda}.x)\) qui se translate vers la droite d’une distance \(\Delta x\) qui augmente avec le temps? Easy game! On l’a rappelé en début de cours, il suffit d’affecter l’abscisse de ce facteur \(\Delta x=vt\). Vous pouvez donc donner l’équation de cette onde sinusoïdale progressive!

\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}(x-vt)\right) \\
\end{align*}

En distribuant, on obtient:

\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{\lambda}vt\right) \\
\end{align*}

Or, par définition (2), on sait que \(v=\frac{\lambda}{T}\):

\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{\lambda}\frac{\lambda}{T}t\right) \\
&= A \ sin\left(\frac{2 \pi}{\lambda}x \ – \ \frac{2 \pi}{T}t\right) \\
\end{align*}

On obtient finalement l’équation de l’onde progressive transversale sous la forme:
\begin{align}
y(x,t) \ = \ A \ sin\left(kx \ – \ \omega t\right) \\
\end{align}

où

• \(k=\frac{2\pi}{\lambda}\) est le nombre d’onde à ne pas confondre avec la constante de raideur d’un ressort (loi de Hooke)
• \(\omega\) est la pulsation de l’onde

Démontrer, c’est bien. Comprendre, c’est mieux!

Cette équation dépend à la fois de la position (x) dans la corde et du temps chrono (t) qui s’écoule.

Périodicité dans le temps

Si vous voulez étudier un point de la corde et observer son oscillation transversale, fixez x à une valeur donnée. Prenons comme exemple \(x=\frac{\lambda}{4} \). Que fait ce point quand le temps s’écoule?

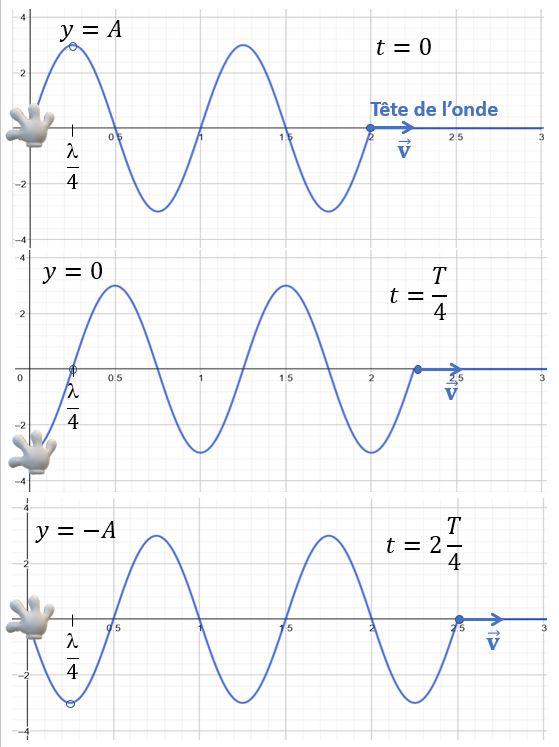
Vous voyez que l’élongation du point de la corde passe de \(y=A\) à \(y=0\), puis à \(y=-A\). On imagine facilement les points suivants: \( 0\) et \(+A\) après respectivement 3/4 de période et une période complète. Un point x de la corde reproduit fidèlement le mouvement périodique (harmonique) de la source qui a créé l’onde qui le traverse. On parle de périodicité dans le temps.
Vérifions le point \(x=\frac{\lambda}{4}\) à deux instants différents: \(t=\frac{T}{4}\) et \(t=\frac{T}{2}\). L’équation \((4)\) devient pour \(t=\frac{T}{4}\) :
\begin{align}
y(\frac{\lambda}{4},\frac{T}{4}) &= A \ sin\left(\frac{2 \pi}{\lambda}\frac{\lambda}{4} \ – \ \frac{2 \pi}{T}\frac{T}{4}\right) \\
&= A \ sin\left(\frac{\pi}{2} \ – \ \frac{\pi}{2}\right) \ = \ 0 \\
\end{align}

Et pour \(t=\frac{T}{2}\) :
\begin{align}
y(\frac{\lambda}{4},\frac{T}{2}) &= A \ sin\left(\frac{2 \pi}{\lambda}\frac{\lambda}{4} \ – \ \frac{2 \pi}{T}\frac{T}{2}\right) \\
&= A \ sin\left(\frac{\pi}{2} \ – \ \pi\right) \\
&= A \ sin\left( \ – \ \frac{\pi}{2} \right) \ = \ -A\\
\end{align}

Périodicité dans l’espace

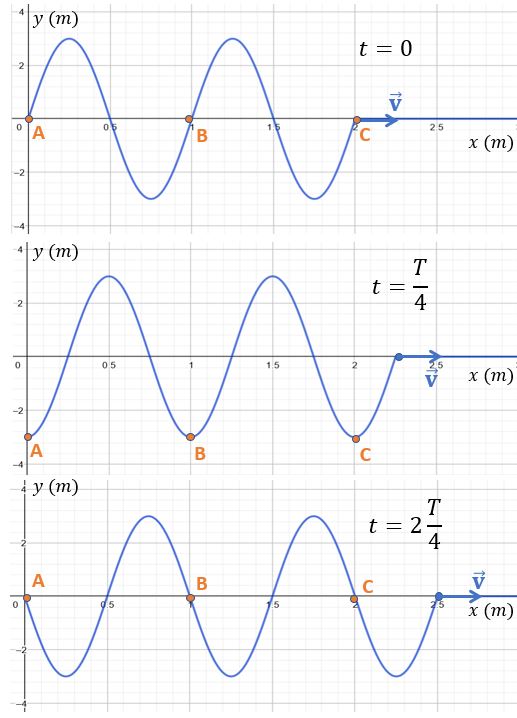
Au lieu de fixer un point de la corde, fixons un temps en prenant une photo à un moment donné, soit \(t=0\).

Concordance de phase

On remarque alors que tous les points situés à une distance d’une longueur d’onde \(\lambda\) les uns des autres, oscillent en concordance de phase. Ils occupent la même élongation aux mêmes moments. Mathématiquement, ceci se traduit avec l’équation de l’onde progressive \((4)\) par:
Pour \(t=0\) :
\begin{align}
y(k\lambda,0) &= A \ sin\left(\frac{2 \pi}{\lambda} k \lambda \ – \ 0 \right) = A \ sin\left(k \ 2 \pi\right) = 0 \\
\end{align}

Il s’agit des points A, B et C repérés en orange dans la figure ci-dessous. Ils sont situés en positions respectives \(x=0\); \(x=\lambda\) et \(x=2\lambda\). Ils occupent la position transversale (le long de Y) d’équilibre et se préparent à descendre vers \(y=-A\). On parle de périodicité dans l’espace.

Et si l’onde se déplaçait vers la gauche et non plus vers la droite?

Vous devriez alors translater la fonction vers la gauche en affectant l’abscisse d’un terme positif. En recommençant le développement (ce qui peut être un bon exercice), vous devriez trouver l’équation d’une onde progressive caractérisée par:

\begin{align*}
y(x,t) &= A \ sin\left(\frac{2 \pi}{\lambda}(x+vt)\right) \\
&= A \ sin\left(kx \ + \ \omega t\right) \\
\end{align*}

Conclusion

L’équation d’une onde transversale progressive se propageant dans le sens du référentiel x (généralement vers la droite), est donnée par:
\begin{align*}
y(x,t) &= A \ sin\left(kx \ – \ \omega t\right) \\
\end{align*}
\(\\\)
L’équation d’une onde transversale progressive se propageant dans le sens opposé au référentiel x (généralement vers la gauche), est donnée par:
\begin{align*}
y(x,t) &= A \ sin\left(kx \ + \ \omega t\right) \\
\end{align*}

avec

• \(k=\frac{2\pi}{\lambda}\) le nombre d’onde à ne pas confondre avec la constante de raideur d’un ressort (loi de Hooke)
• \(\omega\) la pulsation de l’onde

Afin de comprendre ces notions, je ne peux que vous conseiller de vous rendre sur l’excellent site d’animations de physique ostralo.net et de jouer avec l’onde tout en observant le comportement de la source et des différents points de la corde. N’hésitez pas à utiliser les curseurs (blancs) pour plus de clarté. J’exploite également cette animation dans une vidéo YouTube explicative. Bon amusement!

\(\\\) P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile ou s’il reste des zones nébuleuses dans l’article. Merci!