Un fuseau est constitué d’un ventre de vibration en son centre, et de deux nœuds de vibrations (points d’amplitude nulle) aux deux extrémités fixes, comme l’illustre la Fig.3.

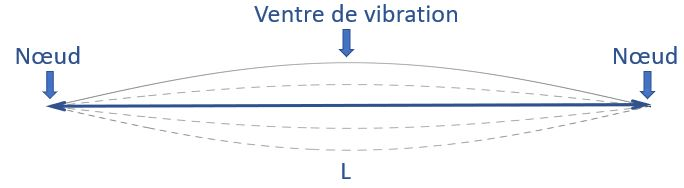
Rmq: Si notre œil est capable de voir ce fuseau, c’est grâce à la persistance rétinienne. En effet, comme chaque point de la corde reproduit le mouvement oscillatoire vertical de la source, chaque point voit sa vitesse s’annuler aux deux extrémités de sa trajectoire verticale et la corde y passe donc globalement plus de temps. Par contre, chaque point de la corde repasse par la position d’équilibre avec une vitesse maximale et c’est donc dans cette position que le fuseau est le moins visible.

IMPORTANT : un fuseau a une longueur égale à une demi-longueur d’onde. En effet, la longueur d’onde a été définie comme la distance parcourue par une onde pendant une période d’oscillation, et pour une onde transversale, elle correspond donc à une sinusoïde complète. Or, un fuseau, c’est une demi-sinusoïde, comme le montre la Fig.4.

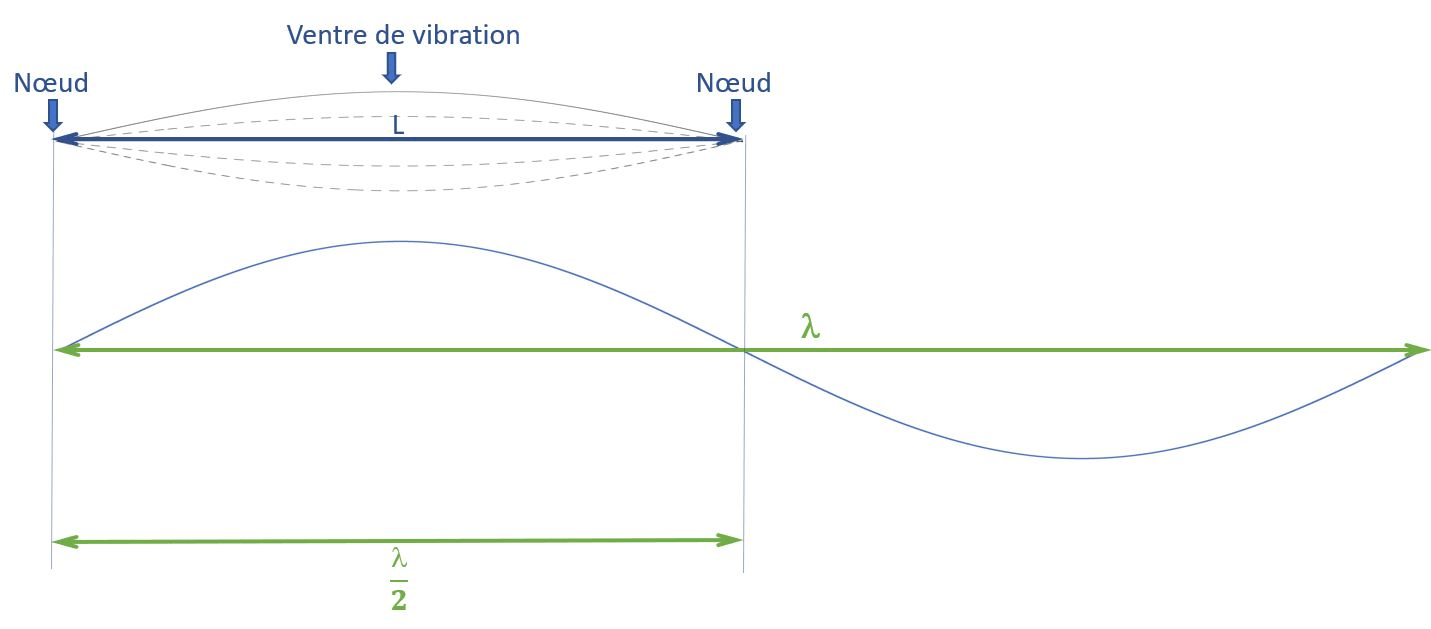
Pour ce mode stationnaire de rang 1, nous pouvons donc écrire :

\begin{equation}
L= \frac{\lambda}{2}
\tag{1}
\end{equation}

Si l’on continue à augmenter la fréquence de vibration de la corde, dans un tout premier temps, le mode stationnaire de rang 1 disparait brusquement pour laisser progressivement apparaitre le mode stationnaire de rang 2 (Fig.5.) lorsque la fréquence atteint 70Hz.

Pour ce deuxième rang, la longueur de corde n’ayant pas été modifiée, on peut écrire :

\begin{equation}
L= \frac{2.\lambda}{2}=\lambda
\tag{2}
\end{equation}

On imagine aisément que si la fréquence de vibration de la corde est amenée à 105Hz, on obtiendra le mode stationnaire de rang 3 pour lequel la longueur de corde correspond à 3 fuseaux (Fig.6) et donc, à \(3.\frac{\lambda}{2}\). On a donc :

\begin{equation}
L= \frac{3.\lambda}{2}
\tag{3}
\end{equation}

On sait que la corde est tendue par le poids de la masse suspendue et que la célérité des ondes transversales qui s’y propagent est donnée par la relation :

\begin{equation}
c= \sqrt{\frac{F_{T}}{\mu}}
\tag{4}
\end{equation}

On connait également la relation fondamentale de la physique ondulatoire qui dit, par ailleurs, que cette célérité est reliée à la fréquence de l’onde et à sa longueur d’onde de la façon suivante :

\begin{equation}
c= \lambda.f\ \Leftrightarrow \ \lambda=\frac{c}{f}
\tag{5}
\end{equation}

Étant donné que la masse linéique (µ) de la corde est une constante (on ne change pas de corde en cours d’expérience), et que la force de tension (\(F_{T}\)) est également constante (la masse suspendue vaut 120g durant toute l’expérience), la célérité doit bien évidemment rester constante, d’après la relation (4).

La masse linéique de la corde est notée ‘µ’, elle correspond à la masse de corde par unité de longueur, càd à la masse d’un mètre de cette corde. Elle s’exprime en \(\frac{[kg]}{[m]}\).

Dès lors, lorsqu’on augmente progressivement la fréquence, la longueur d’onde diminue nécessairement. Les fuseaux sont alors de plus en plus petits.

Remarquons qu’entre les deux premières fréquences de 35 et 70 Hz, la corde oscille de façon aléatoire sans présenter de mode stationnaire. En effet, pour une fréquence de 35Hz, la corde mesurant 1m, la relation (1) nous apprend que la longueur d’onde vaut 2m. Par contre, pour une fréquence de 70 Hz, la relation (2) nous apprend que la longueur d’onde vaut dans ce cas 1 m. En toute logique, lorsque la fréquence augmente progressivement de 35 à 70 Hz, la longueur d’onde diminue progressivement entre 2 et 1m. Étant donné que les deux extrémités sont fixes, elles correspondent obligatoirement à des nœuds, il est dès lors impossible de placer un mode stationnaire sur le mètre de corde dans les conditions intermédiaires comme le montre la Fig.7.

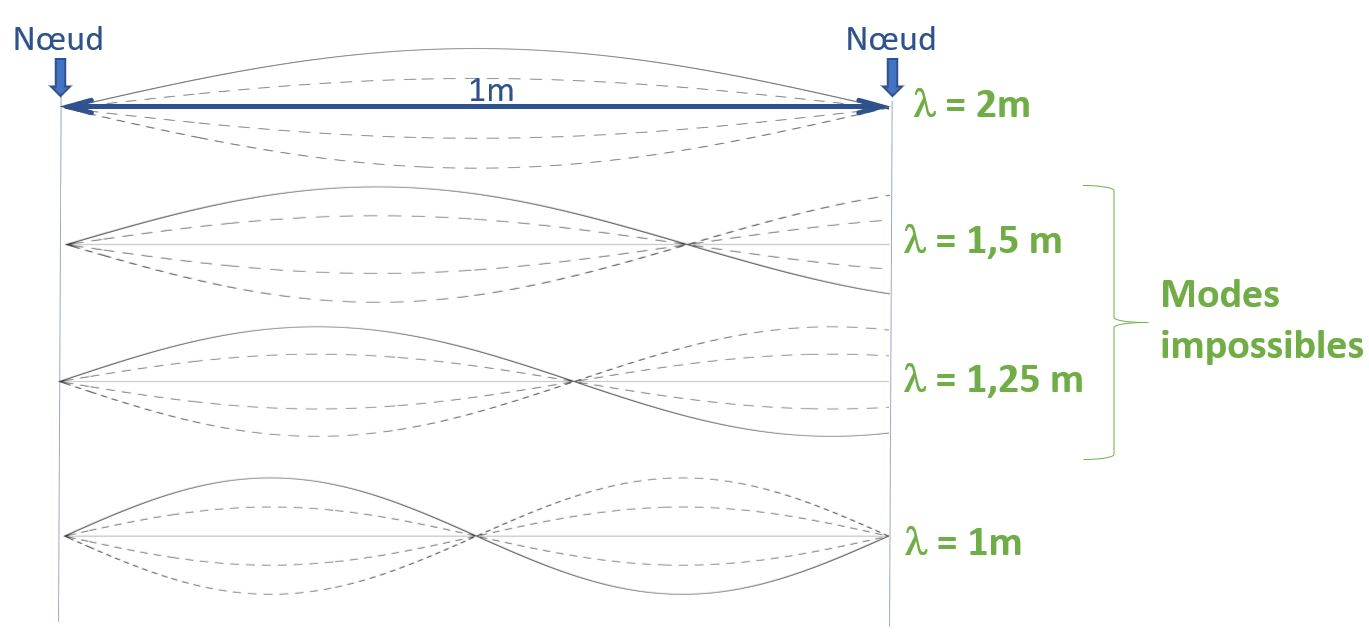
Donc, quand on a une corde tendue entre deux extrémités, seuls certains modes peuvent exister et ils correspondent aux conditions particulières suivantes :

\begin{align}
L &= \frac{\lambda}{2} \\
L &= \frac{2.\lambda}{2} \\
L &= \frac{3.\lambda}{2} \\
\end{align}

Soit,

\begin{equation}
L=n.\frac{\lambda}{2} \, \Leftrightarrow \, \lambda=\frac{2L}{n}
\tag{6}
\end{equation}
où n est le numéro du rang du mode stationnaire, càd le nombre de fuseaux observés.

En combinant les relations (5) et (6), on obtient donc :

\(f=n.\frac{c}{2L}\)

On ajoute souvent un indice n à la fréquence f où n correspond au numéro du rang.

\begin{equation}
f_{n}=n.\frac{c}{2L}
\tag{7}
\end{equation}

Expérience 2 : On augmente progressivement la longueur de corde qui vibre.

En partant du mode de rang 2, ne modifiant ni la fréquence de vibration ni la force de tension, on allonge progressivement la corde. On voit dans un premier temps le mode stationnaire disparaitre, puis pour une longueur de corde de 1,50m précisément, on voit réapparaitre le mode stationnaire de rang 3. Comment peut-on expliquer cela ?

Étant donné que la fréquence et la célérité sont maintenues constantes (on ne touche pas au générateur, on ne change pas de corde, ni la force avec laquelle elle est tendue) ; d’après la relation (5),la longueur d’onde est constante. Par un schéma similaire à celui réalisé sur la Fig.7, on comprend aisément pourquoi le rang 3 fait son apparition lorsque L=1,50m. Les deux rangs intermédiaires qui sont modélisés ne peuvent exister puisqu’ils correspondraient à une extrémité libre alors que la corde est fixée aux deux extrémités.

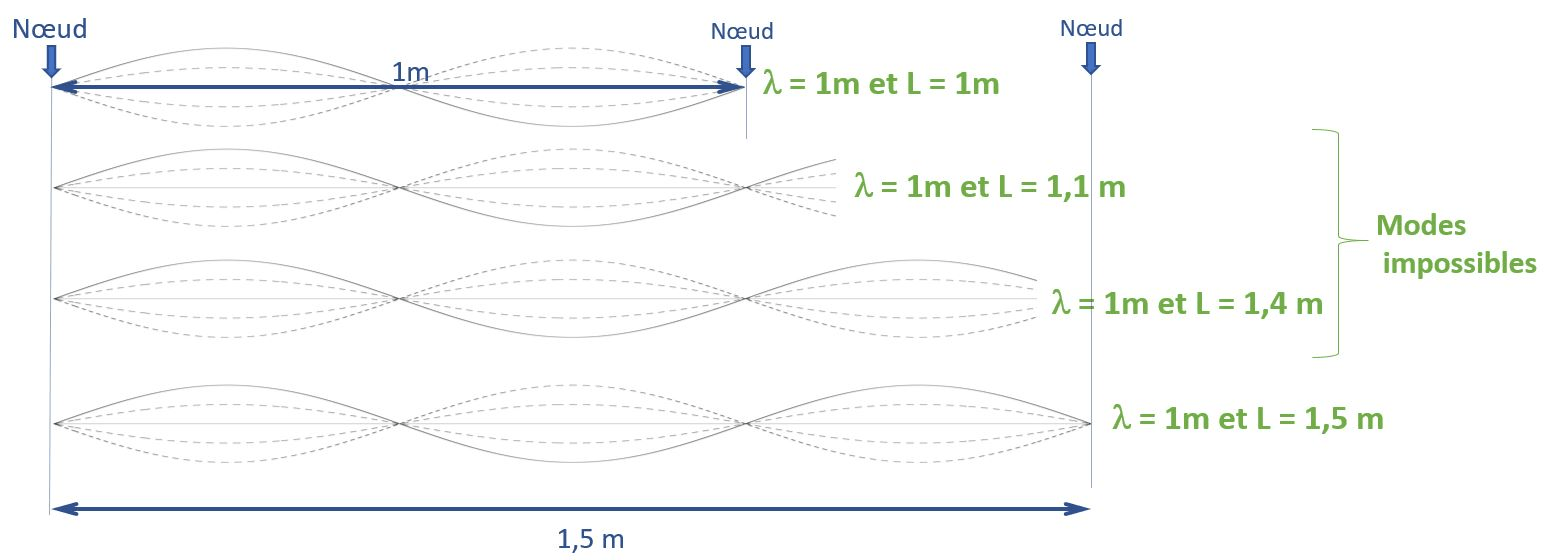
Expérience 3 : On modifie la masse suspendue et donc, la force de tension dans la corde.

On commence avec une longueur de corde de 80cm et une masse suspendue de 30g. La fréquence de vibration est fixée à une valeur telle que le mode de rang 2 apparait dans la corde comme le montre la Fig.9. (Défi : avec toutes les données de cet article, tu dois pouvoir calculer cette fréquence en question !).

En gardant la fréquence inchangée, on modifie la masse suspendue. On remarque que lorsque cette masse est de 70g, aucun mode stationnaire ne peut exister dans la corde (Fig.10)

Par contre, dès que la masse suspendue atteint 120g, soit 4 fois plus qu’en début d’expérience, c’est le mode stationnaire fondamental qui fait son retour !

On ne modifie pas la fréquence au cours de cette expérience. Dans la relation suivante:
\(c= \sqrt{\frac{F_{T}}{\mu}} \, = \, \lambda.f \)

f est une constante.

Par contre, comme la masse de 30 g (exerçant une tension de 0,3N) est remplacée par une masse 4 fois plus grande ; la force de tension est elle aussi quadruplée. On obtient donc :

\(c’= \sqrt{\frac{4F_{T}}{\mu}} \, = \, 2. \sqrt{\frac{F_{T}}{\mu}} \, = \, 2.c \, = \, 2.\lambda.f \, = \, \lambda’.f \)

Et on a donc:

\( \lambda’ \, = \, 2.\lambda \)

Comme, f est constante, on observe donc que la longueur d’onde double. Un fuseau mesure désormais 1m (au lieu de mesurer 0,5m) et correspond donc à la longueur entière de la corde. Avec cette nouvelle force de tension, le mode stationnaire fondamental peut donc exister.
Si on choisissait une force de tension quelconque comprise entre 0,3N et 1,2N, la longueur d’onde aurait une valeur comprise entre 1m et 2m et un fuseau mesurerait alors entre 0,5 et 1m. Aucun mode stationnaire ne pourrait donc exister pour cette longueur d’onde et cette fréquence.

\(\\\)

Pour voir les expériences en vidéo sur ma chaine YouTube, Clique ici!