Bonjour à toutes et à tous,
Aujourd’hui, vous allez apprendre à identifier des forces. Pourquoi? Et bien, pour la simple et excellente raison que les exercices de dynamique que vous devrez réaliser cette année font appel à cette compétence! Je dirais même que c’est LE point de départ de tous ces exercices!
Bien que ce ne soit pas compliqué, bien des élèves paniquent, certains allant jusqu’à inventer des forces: la roue, le volant, la main … Du coup, une petite précision s’impose!
\(\\\)
Comme souvent, il suffit de faire les choses avec calme et rigueur! Voilà la procédure à suivre:
\(\\\)

\(\\\)
1. Identifier LA masse sur laquelle porte l’exercice
\(\\\)
Même si ce point vous parait élémentaire, certains élèves n’hésitent pas à identifier 10 forces qui agissent sur presque autant de masses, de quoi s’emmêler les pinceaux! Si on vous demande d’étudier l’accélération d’un objet en particulier, focalisez toute votre attention sur sa masse et oubliez tout le reste! N’hésitez pas à colorier ou hachurer cette masse.

\(\\\)
2. Identification des forces à distance
\(\\\)
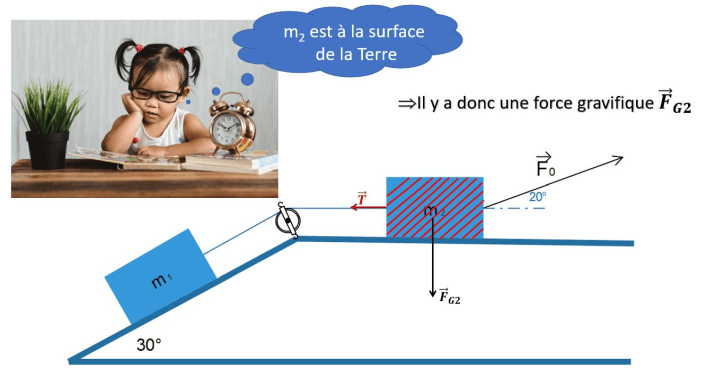
Si l’exercice se passe à proximité de la surface de la Terre ou d’une planète quelconque, la première force à laquelle il faut penser est la force gravifique (ou force poids, ou force pesanteur, ou force gravitationnelle). Cette force est tellement importante qu’on l’appelle de mille et une façons! Enfin, là, j’exagère peut-être un peu, mais je viens quand même de vous donner quatre appellations différentes pour une seule et même bestiole! Comme vous le savez déjà, c’est une force agissant à distance. La Terre n’a pas besoin de vous toucher pour exercer sur vous sa force d’attraction. Si vous en doutez, sautez donc de votre bureau!
\(\\\)
\(\\\)
Nous rencontrerons deux autres forces qui agissent à distance:
- la force électrique qui s’exerce entre deux charges électriques (par exemple un proton et un électron)
- et la force magnétique qui s’exerce entre deux aimants par exemple.
\(\\\)
Voilà donc pour les forces qui agissent à distance.
3. Identification des forces de contact
Pour ce faire, il y a une seule question à se poser: QUI TOUCHE LA MASSE SUR LAQUELLE JE FAIS L’ETUDE DES FORCES? Et sur personne d’autre!
Si vous étudiez le comportement des roues à la surface du sol et que vous me dites que le volant exerce une force sur les roues, alors là, vous vous prenez pour Dieu le Père! Le volant sur lequel vos mains exercent une force, agit via le système de direction sur la direction des roues qui vont solliciter différemment les forces de frottement avec le sol. Ce sont donc les forces de frottement qui agissent sur la roue et non pas le volant qui ne peut pas agir à distance sur les pneus! Vous saisissez l’idée? On parle donc ici de forces de contact!
La réponse à la question « Qui touche la masse étudiée? » ou en langage plus technique « Quelles sont les forces de contact en présence? » est assez simple. Il suffit d’ouvrir grand les yeux et d’observer!
- Une corde peut tirer sur la masse et exercer une force de tension ou de traction.
- Une main peut toucher l’objet et exercer une force de poussée ou de freinage.
- Un pied peut toucher, pendant une fraction de seconde, un ballon pour le lancer au loin tout en le déformant. Nous la noterons \(\overrightarrow{F}_{Pied/Ballon}\) pour bien montrer qu’il s’agit d’une force exercée par le pied sur le ballon (qui est la masse étudiée).
- De façon plus subtile, la masse peut évoluer dans un fluide (l’eau ou l’air) et être soumise à des forces de frottement de type fluide. Toutefois, dans la plupart des cas étudiés, la vitesse du corps est suffisamment faible pour que cette force soit négligée.
- La force gravifique exercée par la Terre sur le centre de gravité du bloc est la seule force qui agit à distance.
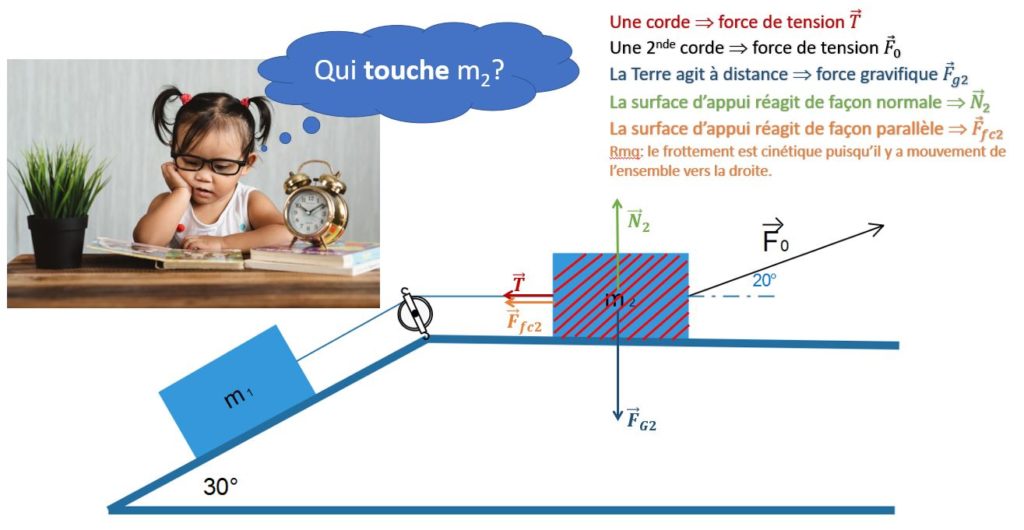
- La corde de gauche touche la masse étudiée et elle exerce donc sur cette dernière une force de tension.
- La corde de droite tire sur le bloc et exerce une force de tension notée \(\overrightarrow{F}_{0}\) à un angle de 20°.
- La surface d’appui réagit de façon normale via \(\overrightarrow{N}_{2}\) et de façon parallèle via \(\overrightarrow{F}_{fc2}\).
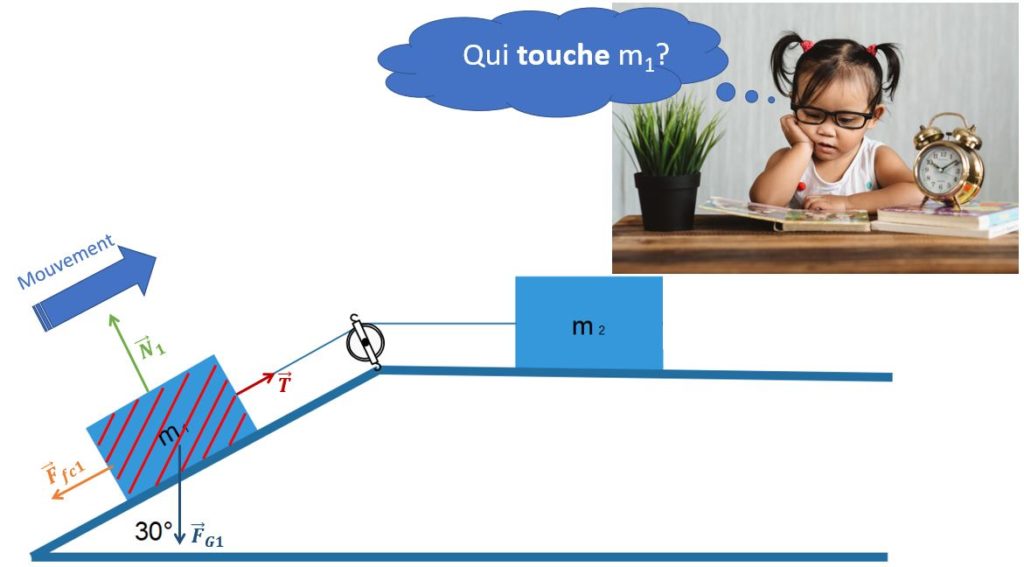
- La force gravifique exercée par la Terre sur le centre de gravité du bloc est la seule force qui agit à distance.
- La corde de droite touche la masse étudiée et elle exerce donc sur cette dernière une force de tension.
- La surface d’appui réagit de façon normale via \(\overrightarrow{N}_{1}\) et de façon parallèle via \(\overrightarrow{F}_{fc1}\).

\(\\\)
 \(\\\)
\(\\\)
\(\\\)
 \(\\\)
\(\\\)
\(\\\)
4. Deux forces de contact importantes: la réaction normale et la force de frottement (statique ou cinétique)
\(\\\)
D’après la loi des actions réciproques (anciennement appelée Action/Réaction) de Newton, on sait que dès qu’une masse prend appui sur une surface, cette surface réagit sur la masse en question. La surface de contact peut réagir de deux façons:
4.1. La réaction normale
\(\\\)
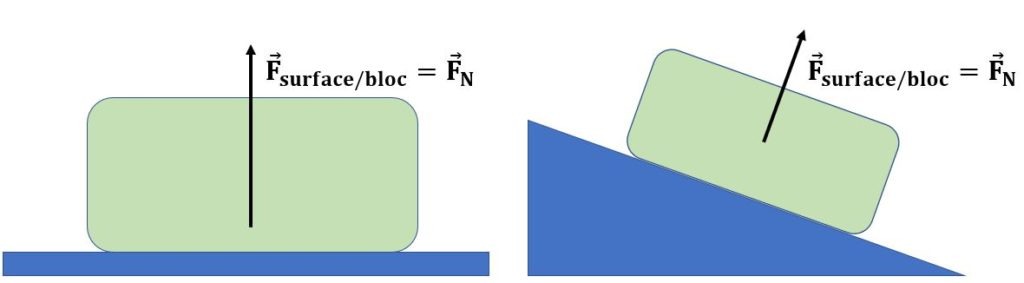
En physique, l’adjectif normal signifie tout simplement perpendiculaire. Ainsi, si une masse prend appui sur une surface, cette dernière réagit en exerçant sur la masse une force perpendiculaire à la surface de contact. Cette force peut s’appeler force normale ou réaction normale. On la notera \(\overrightarrow{F}_{N}\), \(\overrightarrow{R}_{N}\) ou encore \(\overrightarrow{N}\). On rencontre deux cas de figure: soit la surface est plane et la réaction normale possède la même direction que la force d’appui; soit la surface est inclinée et les directions des deux forces dont il est question sont différentes comme le montre la figure ci-dessous. \(\\\)
 \(\\\)
\(\\\)
4.2. La force de frottement
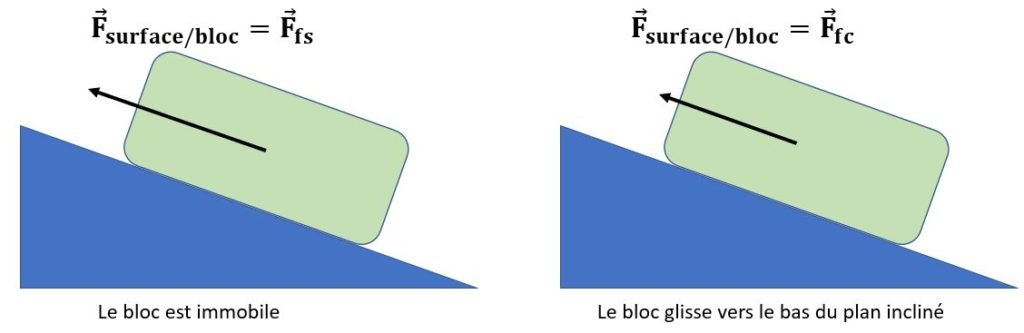
Il s’agit également d’une réaction de la part de la surface d’appui, mais elle n’est plus normale cette fois (càd perpendiculaire), mais bien parallèle à la surface de contact. Si la masse étudiée glisse sur sa surface d’appui on parlera de force de frottement cinétique ou dynamique. A l’inverse, si le bloc, bien qu’il ait tendance à glisser, est maintenu immobile, on parle alors de force de frottement statique. Un article a précédemment été rédigé sur les forces de frottement statique ou cinétique.
\(\\\)
 \(\\\)
\(\\\)
Conclusion
Etudions une masse \(m_{2}\) qui est tractée par une corde faisant un angle de 20° et qui est en mouvement vers la droite, la procédure nous donne ceci:
\(\\\)
\(\\\)
Qu’en est-il de \(m_{1} \)?
La procédure nous donne ceci:
\(\\\)
Et voilà, c’était pas si compliqué! Dans un prochain article, je vous proposerai des exercices pour vérifier votre niveau de compréhension! A bientôt!

\(\\\) P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile. Merci!






