Le travail d’une force: comment le calculer et que signifie-t-il vraiment??
Voici le plan de l’article:
- Définition du travail d’une force
- Notion de système
- Relation mathématique du travail d’une force
- Résolution de deux exercices typiques
- Ce que je retiens …
\(\\\)
Si tu es plus auditif que visuel, cette matière est également disponible sous format vidéo sur YouTube!
1. Définition du travail d’une force
Que dit la définition?
Le travail d’une force traduit les échanges d’énergie qui s’opèrent sur un système en mouvement, d’un point A vers un point B.
Alors, soyons clairs, si vous voulez retenir cette définition par cœur, ça ne sert absolument à rien! Par contre, prenez le temps de la relire et de la comprendre. Que nous dit-elle? Qu’une force qui travaille, c’est une force qui opère des échanges d’énergie. Et des échanges d’énergie sur qui? Sur un système en mouvement.
OUch… Il nous faut donc bien comprendre la notion de système avant d’aller plus loin!
2. Notion de système
En dynamique, on travaille sur des masses ponctuelles. Quand on aborde un problème de façon énergétique (càd via les travaux des forces), on considère plutôt des systèmes qui sont parfois un ensemble de masses. Exemple!
Une pomme tombe à la surface de la Terre

En dynamique, on regarderait la masse ponctuelle de la pomme seule. Ici, on considère le système pomme-Terre et on regarde l’énergie qui lui est apportée ou reprise. C’est un cas de figure un peu particulier, on en reparlera quand on étudiera l’énergie potentielle gravifique dans un prochain chapitre!
Des blocs en mouvement sur un plan incliné
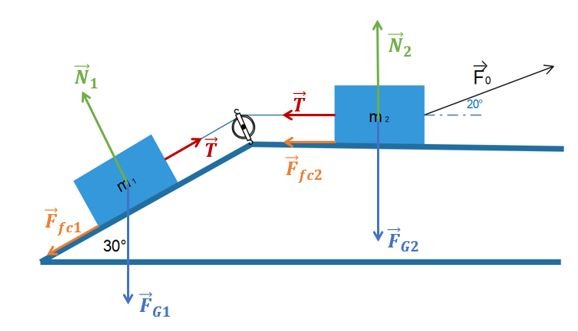
Dans ce cas, plusieurs systèmes sont envisageables:
- On considère uniquement la masse \(m_{2}\):
- On considère les deux masses et le câble qui les relie:
- On comprend aisément que l’agent \(F_{1}\) est de loin le plus efficace. Pourquoi? Parce qu’il exerce sa force tip-top dans la bonne direction! Aucun Newton n’est perdu, ils sont tous efficaces, jusqu’au dernier, pour faire avancer le wagon! Le transfert d’énergie sera maximal!
- A l’inverse de \(F_{1}\), l’agent \(F_{4}\) s’oppose au déplacement du wagon! Cet agent reprend de l’énergie au système au lieu de lui en donner!
- L’agent \(F_{5}\) ne sert strictement à rien. Tirer perpendiculairement aux rails ne peut en aucun engendrer le déplacement du wagon le long de ces derniers. Cet agent n’en touche pas une question énergie!
- Les agents \(F_{2}\) et \(F_{3}\) sont dans le bon, mais, même s’ils exercent exactement la même force que l’agent \(F_{1}\), on est bien d’accord pour dire qu’ils sont un tantinet moins efficaces! Certains de leurs Newtons seront perdus… Ils transfèrent de l’énergie au wagon mais pas autant que \(F_{1} \)
- La force gravifique \(\overrightarrow{F_{g}}\)
- Le sol qui réagit à l’appui du carton \(\overrightarrow{F_{N}}\)
- Le sol qui réagit au glissement \(\overrightarrow{F_{fc}}\)
- La corde qui se tend \(\overrightarrow{F}\)
- \(W_{F_{g}}=0\) car \(\overrightarrow{F_{g}} \perp \overrightarrow{d} \Rightarrow \) la force gravifique est incapable de transférer de l’énergie au système-carton
- \(W_{F_{N}}=0\) car \(\overrightarrow{F_{N}} \perp \overrightarrow{d} \Rightarrow \) la force normale est incapable de transférer de l’énergie au système-carton
- \(W_{F_{fc}}=F_{fc}.d.cos(\theta)=100.3.(-1)= \ – 300 J \Rightarrow \) la force de frottement cinétique transfère 300J en dehors du système-carton, autrement dit, elle les lui reprend
- \(W_{F}=F.d.cos(\theta)=500.3.(0,866)= \ + 1299 J \Rightarrow \) la force de traction transfère 1299J au système-carton, autrement dit, elle les lui donne
- Un travail, c’est un transfert d’énergie (d’une force à un système)
- Une force qui ne déplace pas son point d’application ou une force qui agit perpendiculairement au déplacement, ne travaille pas.
- La direction avec laquelle la force agit par rapport au déplacement du système la rend plus ou moins efficace pour transférer de l’énergie.
- Un travail s’exprime en JOULE, càd en Newtonmètre.
dans ce cas, toutes les forces qui agissent sur la masse sont des forces externes.
dans ce cas, la force de tension devient une force interne, mais nous reparlerons de tout cela prochainement.
Quand on étudiera le travail d’une force, il nous faudra être très clair sur la force considérée ET le système sur lequel elle agit!
3. Relation mathématique du travail d’une force
Essayons d’abord de comprendre de façon intuitive la notion de travail
Il s’agit d’étudier le système « Wagon » pour lequel on souhaite un mouvement vers l’avant (de A vers B). Pour ce faire, 5 agents sont à l’œuvre.
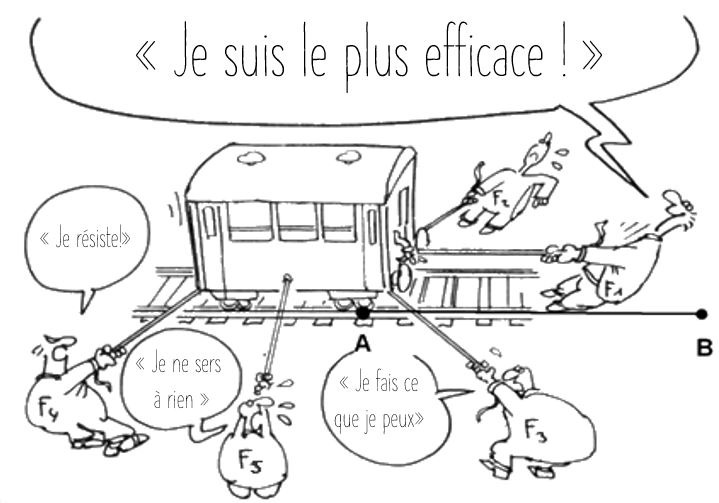
Ce superbe dessin ne m’appartient pas. Je le retrouve sur bien des sites de physique mais j’aimerais savoir qui l’a réellement dessiné! Bravo à lui (à elle), je l’adore, ce dessin!!
Passons aux choses sérieuses: la relation mathématique du travail d’une force!
On vient de pressentir que la valeur de la force, si elle a de l’importance, n’est pas la seule à prendre en considération. Il faut aussi s’intéresser à la direction de cette dernière par rapport au déplacement du système.
Petit rappel!
Mini rappel, même! Si vous ne savez plus ça, vous êtes foutus!
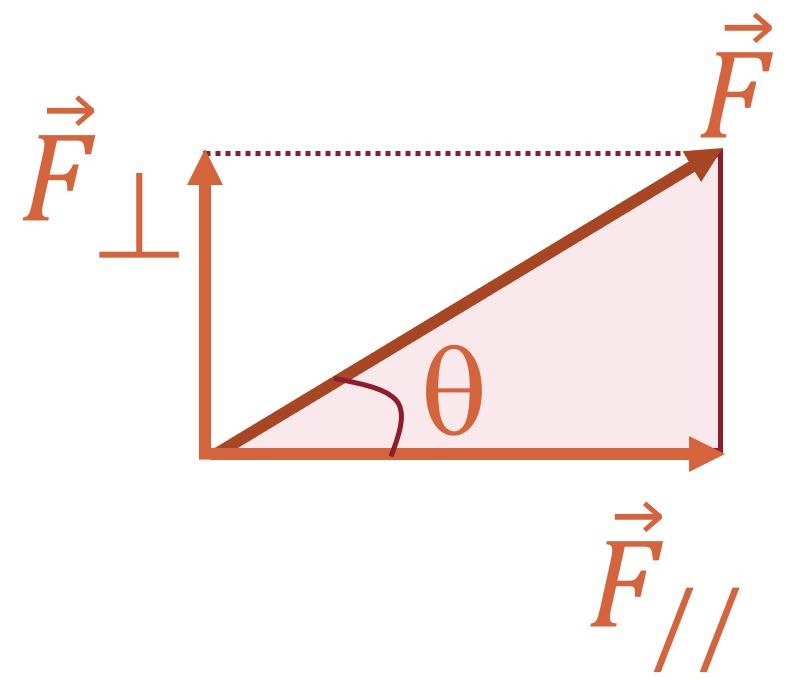
Un vecteur (force, ici) peut toujours être décomposé en deux composantes perpendiculaires: \(\overrightarrow{F_{//}}\) et \(\overrightarrow{F_{\perp}}\). On voit en effet que, si on ajoute le vecteur \(\overrightarrow{F_{\perp}}\) à la suite du vecteur \(\overrightarrow{F_{//}}\), on reforme le vecteur \(\overrightarrow{F}\).
\(\\\)
Mathématiquement parlant, on peut donc écrire:
\(\overrightarrow{F} = \overrightarrow{F_{//}} + \overrightarrow{F_{\perp}}\)
On peut donc, sans stress, travailler avec les deux composantes plutôt qu’avec le vecteur de départ.
\(\\\)
Si vous observez le triangle rectangle, vous pouvez y écrire la relation du cosinus. On obtient:
\(cos(\theta)=\frac{F_{//}}{F} \Leftrightarrow F_{//}=F.cos(\theta)\)
Ok, on garde ça bien au chaud, on y revient dans 35 secondes!
On peut écrire la relation mathématique là, non?
On a dit précédemment que c’est l’orientation de la force par rapport au déplacement qui permet de caractériser son efficacité. Regardons le schéma ci-dessous.
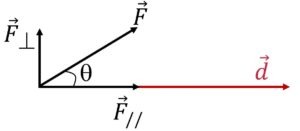
Imaginez que cette force agisse sur un système qui se déplace horizontalement vers la droite, le long du vecteur déplacement (noté \(\overrightarrow{d}\)).
On comprend aisément, que seule la composante \(\overrightarrow{F_{//}}\) de cette force participe au déplacement du système. On dira que, seule cette composante travaille.
La valeur du travail, càd la quantité d’énergie transférée au système dépend donc de la valeur de \({F_{//}}\), mais également de la distance sur laquelle cette force agira. On peut donc, en toute logique donner (enfin!) la relation mathématique du travail d’une force:
La relation mathématique qui définit le travail d’une force est:
\(\\\)
\(W_{F} \ = \ F.d.cos(\theta) \ = \ F_{//}.d\)Point de vue des unités, nous pouvons écrire:
\(J=N.m\)
Les Physiciens ont décidé de rendre hommage à James Prescott Joule (tout un programme), en renommant le Newtonmètre, le JOULE!
On a bien dit que le travail était une notion de transfert d’énergie, non? Quoi de plus normal que de l’exprimer dans cette unité!
\(\\\)
Une petite remarque: ne vous laissez pas influencer par ce qu’on dit dans la vie de tous les jours. Les étudiants ont souvent tendance à associer la notion de travail à celle de fatigue. Or, ce n’est pas toujours le cas. Le gars là, juste en-dessous, il a l’air de se fatiguer, mais en physique, pour autant qu’il garde son bras immobile, il ne travaille pas! Impitoyable physique…
\(\\\)

ATTENTION!! Anguille sous roche!
Le déplacement qui intervient dans la formule parait tout simple mais il peut poser problème dans le cas des corps déformables !
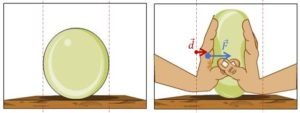
Observons ensemble le cas de figure ci-dessous. Chacune des deux mains exerce une force de 4N et déforme le ballon sur 1,5cm de chaque côté.
\(\\\)
\(\\\)
Dans un premier temps, on peut se dire que, étant donné que le ballon ne se déplace pas, il n’y a pas de travail. C’est faux! En réalité, il y a un détail de toute importance:
Le déplacement dont on parle est celui du point d’application de la force.
Or, on voit clairement (sur la deuxième représentation) que le point d’application de la force appliquée par la main gauche s’est déplacé de 1,5cm. Il y a donc effectivement un transfert d’énergie vers le système ballon. On peut même l’évaluer:
\(\\\)
\(W_{F_{main}}=F_{main}.d_{P.A.}.cos(\theta)=4 \ . \ 1,5.10^{-2} \ . \ cos(0°)= \ + 0,06 J \Rightarrow \) chaque main injecte une énergie de 0,06J dans la balle.
\(\\\)
J’imagine que vous avez remarqué que les \( \textbf{cm} \) ont été transformés en \( textbf{m} \); sans quoi le résultat final ne correspond pas à des Joules mais à du grand n’importe quoi!
4. Exercices
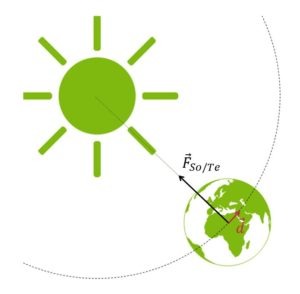
Le mouvement de la Terre autour du soleil
La force d’attraction gravitationnelle exercée pare le Soleil sur la Terre est responsable de la trajectoire circulaire de cette dernière. Le travail que cette force exerce sur le système Terre est-il positif, négatif ou nul?
On voit clairement que la force de gravitation exercée par le Soleil sur la Terre est perpendiculaire au déplacement de cette dernière. Dans ce cas de figure, la force gravitationnelle est donc incapable de transférer de l’énergie au système Terre. Le travail de la force gravifique est nul.
Mouvement d’un bloc tracté sur le sol
On tire sur la corde avec une force de 500N et un angle de 30° par rapport à l’horizontale. Un frottement de 100N agit entre le sol et le carton. Celui-ci se déplace de 3m vers la gauche. Après avoir identifié chacune des forces en présence, détermine le travail qu’elles exercent sur le système carton.
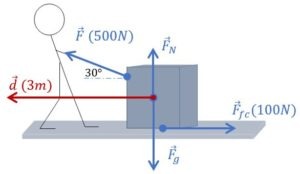
La première étape est la plus importante: il s’agit d’identifier les forces en présence. Si ce n’est pas évident pour toi, je te conseille de relire cet article.
\(\\\)
On a donc:
\(\\\)
On a également dessiné (dans une autre couleur, histoire de ne pas tout mélanger), le vecteur déplacement qui est horizontal et vers la gauche dans cet exercice. Il nous reste donc à appliquer la formule du travail d’une force à chacune des 4 forces en présence.
\(\\\)
Le travail total vaut \(W_{tot}= \ – \ 300 \ + \ 1299 \ \simeq \ + \ 1000 \ J\). Le système carton a gagné \(1000 \ J\) au cours de son glissement de 3m, sous l’influence des forces en présence.
5. Ce que je retiens…
\(\\\)
Dans un prochain article, nous étudierons le résultat d’un transfert d’énergie sur un système et nous parlerons d’énergie cinétique ou d’énergie potentielle.
N’hésitez pas à me laisser un commentaire, qu’il soit positif ou négatif, ou un pouce bleu si l’article vous a plu! Merci!






