Bonjour à toutes et à tous,
Comment réussir tous ses exercices de dynamique? Voilà une question de premier intérêt à laquelle je vais tenter de répondre via l’observation du comportement de mes élèves.
Dans mes classes, il y a trois types de cocos:

- Celui qui se lance tête baissée dans la résolution de tous les exercices du cours et qui les reproduit tellement de fois qu’il les connait par cœur. Ce même élève arrive hyper motivé à l’interrogation et là, c’est la catastrophe! J’ai eu la mauvaise idée de proposer un exercice qui n’a jamais été fait en classe (ce qu’on appelle des exercices de transposition) et c’est la panique à bord! Cet élève qui s’est donné tant de mal et qui se sentait prêt, ne voit absolument pas ce que je lui veux… Il me maudit de tout son être … et je peux le comprendre…
- Celui qui relit son cours en touriste sans jamais se donner la peine d’essayer de refaire le moindre exercice et qui est convaincu que la matière est facile et qu’il va réussir son interro. Si si, ça existe! Comment diable voulez-vous que votre main puisse reproduire en examen ce que vous ne lui avez jamais demandé d’exercer? Connaissez-vous beaucoup de footballeurs brillants qui se contentent de lire un cours sur le tir au but avant de jouer un match? C’est ridicule, non? …
- Et puis … il y a l’élève qui a tout compris! Avant de se lancer dans la résolution des exercices, il relit sa théorie, la comprend (ben oui, quand même!), et essaie d’en dégager l’essence! Puis, seulement quand cette étape cruciale (et gourmande en temps) est passée, il se donne la peine de faire des exercices. Tous les exercices? Que nenni! Il est capable de repérer les différents types d’exercices, et ne refera qu’un ou deux exercices de chaque sorte avant de, éventuellement (laissez-moi rêver), relire le reste des exercices faits en classe pour le plaisir!
\(\\\)
\(\\\)
\(\\\)
J’imagine que je n’ai pas besoin de vous dire lequel des trois est considéré par le reste de la classe comme étant le plus fort? Injustice profonde, parce que cet élève se sera, au bout du compte, donné moins de mal que celui qui aura refait 100 000 exercices! Et re-injustice, il retiendra son cours à bien plus long terme que le pauvre malheureux qui y a consacré tellement de temps… Il y a de quoi déprimer non?
Vous voulez savoir ce qui se passe dans la tête de l’élève de type-3? Alors, lisez ce qui suit!
Synthèse de la théorie
Synthétiser ne signifie pas recopier ce que le prof a mis en caractère gras dans son cours! Synthétiser signifie relire toute la théorie, la comprendre et en prendre quelques notes personnelles.
Le point de départ: \(\Sigma \overrightarrow F = m.\overrightarrow a\)
Le principe fondamental de la dynamique vous dit ceci: \(\Sigma \overrightarrow F = m.\overrightarrow a\). J’ai connu un prof il y a bien longtemps qui disait: « éh les gars, si vous ne savez plus ça, vous êtes perdus hein! Vous ne savez même plus comment vous vous appelez quoi! »… Je dois dire que je suis assez d’accord avec lui. Après tout, le principe dit bien qu’il est fondamental, non?
Regardez ce principe: vous voulez une accélération dans une direction donnée? Et bien il vous faut une force résultante exactement dans cette direction les gars!
\(\\\)
C’est ici qu’une autre question, encore plus fondamentale, se pose! C’est quoi exactement une accélération?
\(\\\)
Là, pendant que l’élève de type-1 se dit qu’une accélération c’est \(\overrightarrow a = \frac{\Delta\overrightarrow v}{\Delta t}\), l’élève de type-2 lui, ne se pose aucune question: il sait que quand il accélère, il va plus vite! Bing! Première erreur! C’est vrai dans la vie de tous les jours ça, mais pas dans le monde du physicien! Pas seulement en tout cas! Ecoutez plutôt ce que se dit l’élève de type-3… Il lit la relation vectorielle en français et se dit: « Une accélération, c’est une variation du vecteur vitesse au cours du temps » (on sait en effet que le \(\Delta\) est le « D » de différence: \(\Delta \overrightarrow v = \overrightarrow v_{2} – \overrightarrow v_{1} \)). Et il sait qu’un vecteur varie si son intensité change (ça, même l’élève de type-2 le sait), mais il sait aussi que si la direction du vecteur change, le vecteur change! Pour un physicien, tourner (même à vitesse constante en norme), c’est accélérer!
\(\\\)
Au passage, un petit truc pour le vecteur vitesse, c’est le plus facile des vecteurs à se représenter: vous imaginez une voiture avec une flèche enfoncée dans le capot avant. Si la voiture avance en ligne droite, le vecteur vitesse ne change pas de direction, mais dès que la voiture tourne, la flèche enfoncée dans son capot tourne avec elle et la direction du vecteur vitesse est modifiée! Le vecteur vitesse est donc tangent à la trajectoire! Toujours!
\(\\\)
Question suivante: Si le vecteur vitesse est enfoncé dans le capot de la voiture, le vecteur accélération, il est où, lui?
C’est un peu plus compliqué pour le vecteur accélération parce qu’il n’a pas toujours la même direction. Alors que l’élève de type-1 est trop occupé à faire ses exercices et que l’élève de type-2 n’en a cure, l’élève de type-3 retourne au début de son cours de physique et relit la construction du vecteur accélération (Vidéo: Construction du vecteur accélération). En gros, il détecte deux sortes d’accélération:
- L’accélération tangentielle: tangentielle parce que parallèle au vecteur vitesse
- Et l’accélération normale: normale parce que perpendiculaire au vecteur vitesse

Pas de stress, voilà ce que l’élève a revu dans son cours:

Une accélération tangentielle correspond donc à une modification de l’intensité du vecteur vitesse. L’intensité du vecteur \(\overrightarrow v_{3}\) est en effet plus grande que l’intensité du vecteur \(\overrightarrow v_{1}\), ce qui conduit à un vecteur \(\Delta \overrightarrow v_{2}\) et donc à un vecteur \(\overrightarrow a_{2}\) de mêmes direction et sens que les vecteurs vitesse.
\(\\\)
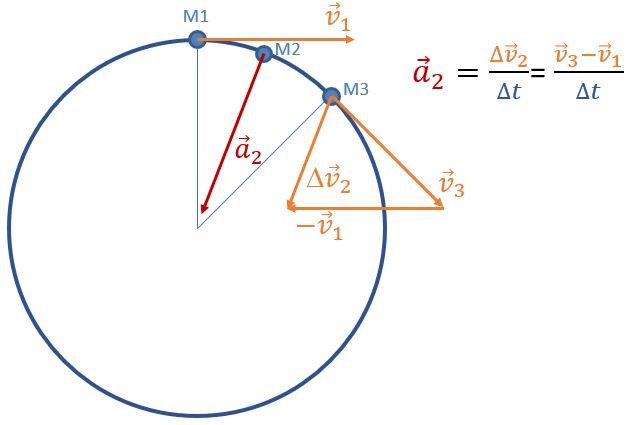
Une accélération normale (dite encore centripète ou radiale) est quant à elle une variation du vecteur vitesse en direction: on tourne! Entre \(\overrightarrow v_{1}\) et \(\overrightarrow v_{3}\), seule la direction du vecteur change, et on voit (par construction vectorielle) que cela conduit à un vecteur variation de vitesse au point 2 (noté \(\Delta\overrightarrow v_{2}\)) et donc à un vecteur accélération \(\overrightarrow a_{2} \) perpendiculaire au vecteur vitesse en ce point 2.
Dernière question: c’est quoi encore le lien entre force et accélération?
L’élève de type-1 est toujours occupé à bosser ses exercices et il en a déjà marre… L’élève de type-2 a fini de réviser depuis longtemps, il renforce les muscles de ses pouces sur sa console de jeux! L’élève de type-3 se rappelle vaguement un truc: une force qui agit sur une masse provoque une accélération d’après la relation \(\Sigma \overrightarrow F = m . \overrightarrow a \). Comme la masse est un scalaire positif, le vecteur accélération possède exactement le même sens et la même direction que le vecteur force résultante (\(\Sigma \overrightarrow F\)). Bingo! Il a tout pigé le gars!
\(\\\)

\(\\\)
Il peut commencer à relire ses exercices pour repérer les différents types possibles et les sélectionner pour les refaire tranquillou le lendemain! … Parce que, oui, j’ai oublié de vous dire: l’élève de type-3 ne s’y prend pas la veille!
Quels sont les différents types d’exercices?
Soit on donne le type de mouvement: Equilibre, MRU, MRUA, MRUD, MCU …
- C’est un équilibre: Je dessine toutes les forces, je choisis le référentiel (x,y) le plus approprié (càd les deux directions perpendiculaires le long desquelles on rencontre le plus de forces) et j’exprime le principe fondamental dans ces deux directions. Il n’y a pas de mouvement donc aucune accélération, on a:
- C’est un MRU: C’est presque pareil, c’est un équilibre dynamique. Je dessine toutes les forces, je choisis le référentiel (x,y) le plus approprié (généralement X est choisi dans le sens du mouvement) et j’exprime le principe fondamental dans les deux directions. La vitesse est constante (en intensité et en direction), il n’y a donc aucune accélération dans la direction du mouvement (X) et aucun mouvement selon Y, donc aucune accélération non plus. On a:
- C’est un MRUA: C’est un peu différent. Il y a une accélération tangentielle, càd parallèle au vecteur vitesse. Si je choisis le référentiel X dans la direction et dans le sens du mouvement, alors, il y a une accélération le long de ce référentiel X que je note donc \(a_{x}\). Par contre, le mouvement étant rectiligne, il n’y a aucun mouvement et donc aucune accélération dans la direction Y. Je dessine toutes les forces et j’exprime le principe fondamental dans les deux directions:
- C’est un MRUD: C’est presque pareil, il y a aussi une accélération tangentielle mais opposée à la vitesse (on parle d’ailleurs de décélération). Je dessine toutes les forces, je choisis le référentiel (x,y) le plus approprié (X est toujours dans le sens du mouvement) et j’exprime le principe fondamental dans les deux directions:
- C’est un MCU: C’est carrément différent, il y a ici une accélération normale, càd perpendiculaire à la vitesse. Je dessine toutes les forces, je choisis le référentiel (x,y) le plus approprié (cette fois, le référentiel X doit être choisi vers le centre du mouvement puisque c’est dans cette direction que se produit l’accélération) et j’exprime le principe fondamental dans les deux directions:
\(\Sigma F_{x} = 0\) et \(\Sigma F_{y} = 0\)
\(\Sigma F_{x} = 0\) et \(\Sigma F_{y} = 0\)
\(\Sigma F_{x} = m.a_{x}\) et \(\Sigma F_{y} = 0\).
\(\Sigma F_{x} = m.a_{x}\) et \(\Sigma F_{y} = 0\). On devra trouver une composante scalaire \(a_{x} < 0\) puisque le vecteur est opposé au référentiel X!
\(\Sigma F_{x} = m.a_{cp} = m.\frac{v²}{R}\) et \(\Sigma F_{y} = 0\). En effet, dans un MCU, seule la direction de la vitesse change, il ne faut donc de force résultante (et donc d’accélération) que perpendiculairement à la vitesse, vers le centre du mouvement!
Soit on ne donne pas précisément le type de mouvement
Dans ce cas, en fonction de l’énoncé, on choisit des référentiels judicieux (on sait au moins si le mouvement est rectiligne ou circulaire). On dessine les forces et on calcule la résultante le long de chacune des deux directions X et Y: on en déduit le type de mouvement!
- Il y a une force résultante dans le sens du mouvement ? \(\Rightarrow\)c’est un MRUA
- Il y a une force résultante opposée au mouvement ? \(\Rightarrow\)c’est un MRUD
- Il y a une force résultante perpendiculaire à la vitesse ? \(\Rightarrow\)c’est un MCU
- Il y a une force résultante oblique par rapport au vecteur vitesse ? Il y a donc une composante tangentielle de la force qui va provoquer une accélération tangentielle, càd une modification de l’intensité du vecteur vitesse (la norme de la vitesse varie) et une composante normale de la force qui va provoquer une accélération normale càd une modification de la direction du vecteur vitesse (le mouvement est curviligne)\(\Rightarrow\)c’est un MCV
A ce stade, l’élève de type-1 n’a pas fini ses exercices et se sent complètement dépassé, l’élève de type-2 en est à sa ènième partie de Fortnite et l’élève de type-3 peut faire ce qu’il veut!
\(\\\)
Alors, à vous de jouer!!!!

J’espère que cet article vous a été utile? Si c’est le cas, n’hésitez pas à le liker! Mieux encore, laissez-moi un commentaire que je connaisse vos impressions (bonnes ou mauvaises)! 😉 Merci!





