Voilà LA notion scalaire par excellence en physique, celle de travail ! Mais attention, une fois de plus, le langage usuel (que vous utilisez donc tous les jours à longueur de temps) entre en contradiction avec le langage physique (que vous utilisez certains jours, de temps en temps) ! En effet, dans la vie de tous les jours, si j’avance avec un bloc pesant en main, à vitesse constante, je travaille parce que je me fatigue. Dans la vie du physicien, je peux, dans ces conditions, me balader 2 heures avec un bloc, aussi pesant soit-il dans les mains, je ne travaille pas ! Aïe, ça commence fort ! Il va donc falloir être vigilant pour ne pas se laisser piéger…
Commençons donc par une précision de vocabulaire : Dans le langage courant, on parle de travail intellectuel, de travail physique, de travail scientifique … le physicien, lui, parlera uniquement du travail mécanique d’une force et il le notera W pour « Work ».
La capacité qu’a une force à effectuer un travail mécanique est parfois définie comme étant l’énergie; mais dans certains cas, l’énergie ne peut être complètement transformée en travail ; cette définition a donc ses limites. Quoi qu’il en soit, la notion de travail mécanique est intimement liée à celle d’énergie et le travail s’exprime d’ailleurs dans la même unité, soit, le JOULE [J].
En réalité, l’énergie est une notion abstraite (ce n’est pas une substance) et elle a un truc particulier, elle est capable de se transformer d’une forme en une autre mais elle ne peut jamais disparaitre ni soudainement apparaitre ; on dit qu’elle se conserve.
Définition du travail effectué par une force constante

Définition : Le travail W effectué par une force constate (F) dont le point d’application se déplace sur une distance d est défini par la relation scalaire W = F.d
En observant cette première définition, on constante que le Joule [J] est égal au Newton.mètre [Nm]
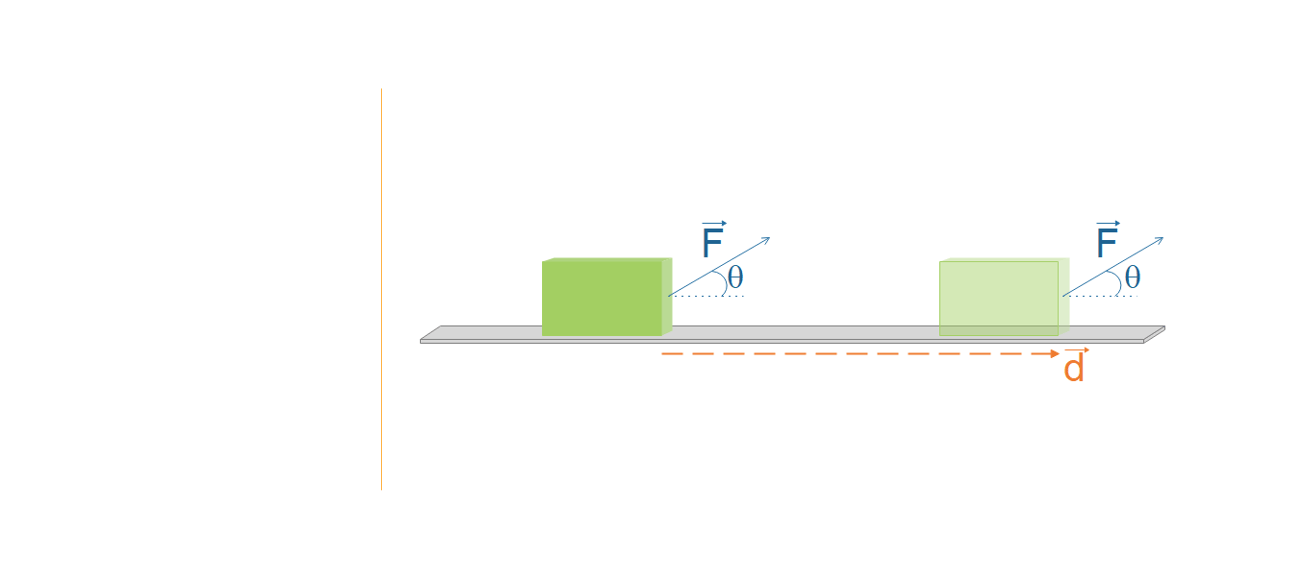
Qu’en est-il de la situation suivante ? La force appliquée \(\overrightarrow{F} \) est-elle plus ou moins efficace pour faire avancer le bloc ?

Moins efficace bien entendu puisque, seule la composante de cette force parallèle ou tangentielle au mouvement est responsable du mouvement du bloc. On donnera donc une définition plus complète du travail :
\( W = F.d.cos\theta\) où \( \theta \) est l’angle compris entre la direction du vecteur force ( \(\overrightarrow{F} \)) et la direction du vecteur déplacement ( \(\overrightarrow{d} \)).
Ceux qui ont étudié le produit scalaire dans leur cours de math, verront qu’il s’agit d’un produit scalaire et que le travail d’une force est donc au final défini par :
\( W = \overrightarrow{F}.\overrightarrow{d} \tag 1\\\)
3 cas de figure peuvent se présenter :

1. La force est appliquée à un angle < 90° par rapport au déplacement \( \Rightarrow \) elle effectue un travail positif dit moteur car la force possède une composante dans le sens du mouvement :
si \( \theta \) < 90° \( \Rightarrow \)\(\overrightarrow{F_{tg}} \) // \(\overrightarrow{d} \) \( \Rightarrow \) W > 0
2. La force est appliquée à un angle > 90° par rapport au déplacement \( \Rightarrow \) elle effectue un travail négatif dit résistif car la force possède une composante qui s’oppose au mouvement :
si \( \theta \) > 90° \( \Rightarrow \)\(\overrightarrow{F_{tg}} \) <> \(\overrightarrow{d} \) \( \Rightarrow \) W < 0
3. La force est appliquée précisément à 90° par rapport au déplacement \( \Rightarrow \)elle n’effectue aucun travail:
si \( \theta \) = 90° \( \Rightarrow \) W = 0
Dès lors, la réaction normale qui agit sur un bloc qui glisse le long d’un plan incliné n’effectue aucun travail, de même que la force de tension qui fait tourner la fronde autour de la main (elle est toujours perpendiculaire au déplacement, à chaque instant).
Remarquons qu’il nous manque un cas de figure particulier : celui où une force est exercée mais il n’y a aucun déplacement, dans ce cas, le travail est également nul (d’après la définition puisque d=0) ; même si l’agent qui exerce la force se fatigue. Faites bien la différence entre travail physiologique non nul (celui des muscles qui se fatiguent pour maintenir l’haltère en l’air par exemple) et le travail mécanique nul (celui de la force exercée par l’haltérophile sur l’haltère). Mécaniquement, que l’haltère soit maintenu à une certaine altitude par un homme ou un support fixe, c’est exactement la même chose.
Si plusieurs forces agissent simultanément sur un corps qui se déplace, le travail total sera donné par la somme des travaux de chacune de ces forces :
\[ W_{tot} = \Sigma \overrightarrow{F}.\overrightarrow{d} \]
ATTENTION : Dans la plupart des cas, les forces de frottement cinétique (« Rappel ») agissent dans le sens opposé au glissement, \( \theta \) vaut donc 180° et le travail des forces de frottement est négatif ou résistif. Toutefois, dans certains cas (le tour de magie nappe/assiettes par exemple); le frottement agit dans le sens du déplacement et donc, le travail des forces de frottement est moteur! Ne vous laissez pas avoir ! Pensez au truc pour identifier le sens de la force de frottement cinétique! (« Rappel »)
Remarquons encore, ce sera utile par la suite, que la notion de travail peut être représentée par l’aire située sous la courbe de la force en fonction du déplacement:

Pour un déplacement \( \Delta d = d_{2} – d_{1}\), le travail de la force \( F_{0}\) vaut \( W=F_{0}.\Delta d\) ; ce qui correspond bien à l’aire du rectangle (Longueur x largeur) représenté sur le graphique ci-contre.
Définition du travail effectué par une force variable sur un déplacement
Dans certains cas, la force change d’intensité au cours du déplacement, c’est typiquement le cas d’un ressort sur lequel on exerce une force de traction. La loi de Hooke nous dit que cette force est directement proportionnelle à l’élongation (x) du ressort. La notion d’élongation correspond à la position de l’extrémité du ressort par rapport à sa position d’équilibre (lorsque le ressort n’est ni allongé, ni comprimé).
\[F_{él} = – k.x \]
k représente la constante de raideur du ressort ; exprimée en [N/m] qui, comme son unité le laisse supposer, correspond à la force qu’il faut exercer sur le ressort pour l’allonger d’un mètre.
Le signe « – » quant à lui existe parce que la force élastique exercée par le ressort s’oppose toujours à l’élongation : si le ressort est comprimé vers la gauche, la force élastique a tendance à le ramener vers sa position d’équilibre (idem si le ressort est étiré vers la droite, la force élastique sera dirigée vers la gauche). Pour cette raison, la force élastique est appelée force de rappel.

Et donc, en partant de la position d’équilibre (x=0), si on étire le ressort vers la droite, une force élastique de plus en plus intense apparait vers la gauche. Cette force est proportionnelle à l’élongation x et est négative dans notre référentiel (le vecteur \( \overrightarrow{F_{él}} \) est en effet de sens opposé au référentiel) ; elle est donc de plus en plus négative comme le montre le graphique suivant.

Dès lors, que vaut le travail de la force élastique au cours d’un déplacement \( \Delta x \)? Afin de pouvoir réutiliser la relation (1) définie au point précédent, on découpe le déplacement en une suite de mini-déplacements appelés déplacements élémentaires et notés \( \Delta x_{i} \) au cours desquels la force est considérée comme constante. En effet, si on allonge faiblement le ressort, la force élastique augmente faiblement et on peut raisonnablement considérer qu’elle reste constante. On se retrouve donc avec une série des petits travaux élémentaires \( \Delta W_{i} \) qui correspondent aux aires des rectangles de largeur \( \Delta x_{i} \) et de longueur \( F_{i} \) .
Le travail total sera donc tout simplement la somme des travaux élémentaires, càd l’aire du trapèze coloré sur le graphique suivant :

Mathématiquement, on sait que l’aire d’un trapèze est donnée par :
\[ \normalsize A = \frac{(B + b).h }{2} \]
Avec:
\begin{align}
B &= F_{f} = \ – k.x_{f} \\
b &= F_{i} = \ – k.x_{i} \\
h &= \Delta x = x_{f} – x_{i} \\
\end{align}
On obtient donc:
\begin{eqnarray}
W_{tot} &=& \frac{(- \; k.x_{f} \; -\; k.x_{i}).(x_{f} \; -\; x_{i})}{2} \\
&=& \frac{(- \; k.x_{f}^{2} \; +\; k.x_{f}.x_{i} \; – \; k.x_{i}.x_{f} \; + \; k.x_{i}^{2})}{2} \\
&=& \frac{- \; k.(x_{f}^{2} \; -\; x_{i}^{2})}{2} \\
\end{eqnarray}
Ceux qui ont reçu un cours de math sur les intégrales reconnaitront que cette somme de travaux élémentaires correspond en réalité à une intégrale dès lors que les intervalles \( \Delta x \) tendent vers zéro et sont alors notés \(dx \) ! Je vous rappelle d’ailleurs que le symbole d’une intégrale \(\int {}\) est un S qui signifie somme !
Pour les plus courageux, on peut donc écrire ceci :
\begin{eqnarray}
W_{tot} &=& \lim_{ \Delta x \to 0} \left( \Sigma (F_{i}.\Delta x_{i}) \right) = \int{F_{i}.dx_{i}} \\
&=& \int \limits_{x_{i}}^{x_{f}} {F_{i}.dx_{i}} \\
&=& \int \limits_{x_{i}}^{x_{f}} {-k.x_{i}.dx_{i}} \\
&=& -k.\int \limits_{x_{i}}^{x_{f}} {x_{i}.dx_{i}} \\
&=& -k.\left[\frac{x_{i}^{2}}{2}\right]_{x_{i}}^{x_{f}} \\
&=& \frac{-k}{2}.\left(x_{f}^{2}-x_{i}^{2}\right) \\
\end{eqnarray}
Yessss!