Quelle est la base à maitriser pour comprendre les interférences?

Il y a trois grandeurs intimement liées les unes aux autres qu’il te faut absolument comprendre:

1. La différence de marche d’une onde par rapport à une autre: \(\delta \),
2. Le retard d’une onde par rapport à une autre: \(\Delta t\),
3. Le déphasage d’une onde par rapport à une autre: \(\Delta \Phi\).

I. La différence de marche \(\delta \)

Commençons avec le grandeur la plus simple: la différence de marche, notée \(\delta \) et définie par \(\delta = d_{2}-d_{1} \).
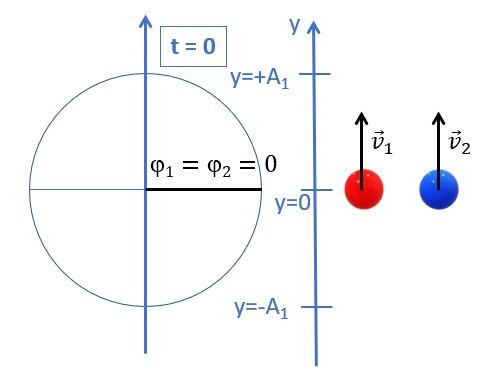
Pour faire simple, considérons deux sources transversales qui vibrent en phase (leur déphasage est nul et constant) à la surface de l’eau dans une cuve à ondes. Elles occupent donc les mêmes positions transversales aux mêmes instants. Quand une source est au sommet de sa trajectoire et s’apprête à descendre; la seconde est exactement dans le même état. Pour faire plus simple encore, considérons qu’à la date t=0; les deux sources se trouvent à leur position d’équilibre et qu’elles s’apprêtent à monter dans le sens du référentiel vertical et orienté vers le haut, appelé Y. Les deux sources vibrent en mouvement harmonique et leurs équations respectives sont données par:
\(y_{S1}(t)=A_{1}sin(2\pi ft)\)
\(y_{S2}(t)=A_{2}sin(2\pi ft)\)

On comprend aisément, en regardant la Fig.1 que la constante de phase \(\phi\) est nulle.

A l’instant t=0, on imagine que la surface de l’eau est plane et que le mouvement harmonique des sources commence seulement. Comme le montre la Fig.2, les deux sources vont générer des crêtes qui vont se propager à vitesse constante dans la cuve à ondes vers un point P quelconque.

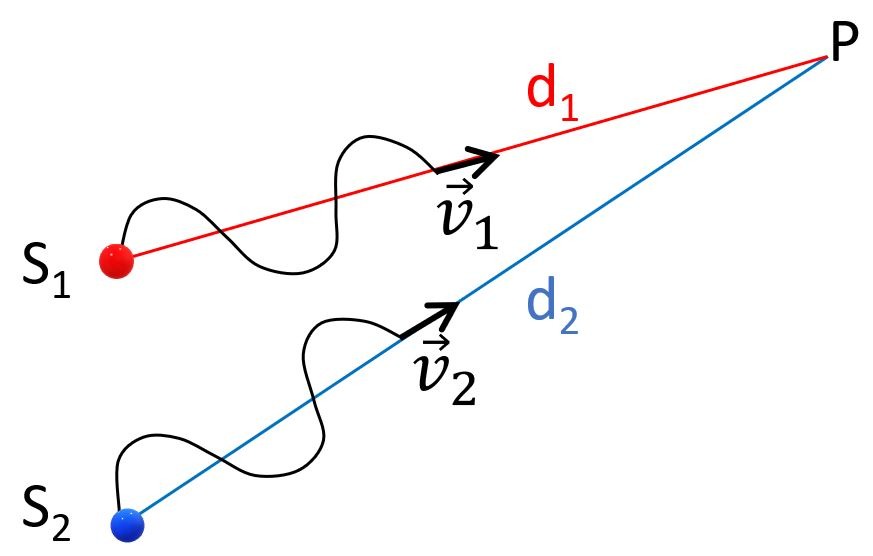
Pourquoi des crêtes?

Parce qu’on a considéré que la constante de phase des sources était nulle. Quand t=0, y=0 et la source monte, elle génère donc une crête.

Pourquoi à vitesse constante?

La norme des deux vitesses est la même puisqu’il s’agit d’ondes de même nature qui se déplacent dans le même milieu.

Qu’est-ce que la différence de marche?

Etant donné le point P choisi, on remarque que la distance \(d_{1}\) que doit parcourir l’onde issue de \(S_{1}\) est plus petite que la distance \(d_{2}\) que doit parcourir l’onde issue de \(S_{2}\) pour atteindre le point P en question. L’onde issue de \(S_{2}\) doit donc « marcher » sur une distance plus grande que l’onde issue de \(S_{1}\). De combien de mètres? D’une distance caractéristique, nommée différence de marche, et définie par \(\delta = d_{2}-d_{1} \).

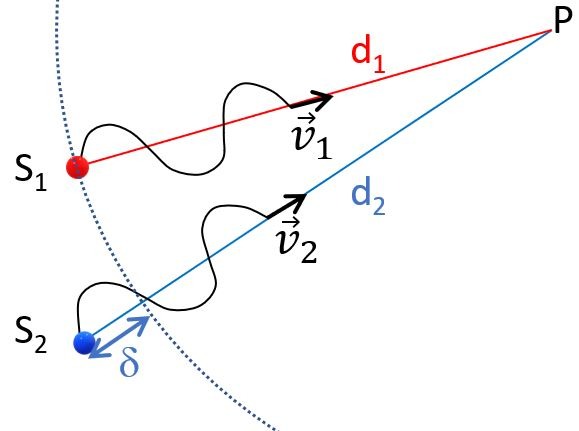
Conséquence?

La première crête issue de \(S_{2}\) atteindra le point P plus tard que celle issue de \(S_{1}\). On pourra donc définir le retard \(\Delta t\) d’une onde par rapport à l’autre.

II. Le retard \(\Delta t\)

Prenons un outil mathématique: le graphique de l’élongation (càd de la position verticale) du point P au cours du temps. A la date t=0, ce point est à la surface d’une eau paisible et il ne bouge pas: y=0. Par contre, après un temps \(t_{1}\), il reçoit la crête issue de \(S_{1}\). Il se met donc à vibrer sous l’influence de cette 1ère onde.
Que se passe-t-il ensuite? La crête issue de \(S_{2}\) finit par arriver après un temps \(t_{2}\). A partir de cet instant, le point P reçoit deux ondes qui se superposent. On dit qu’elles interfèrent. Le point P vibre comme l’addition des deux ondes.

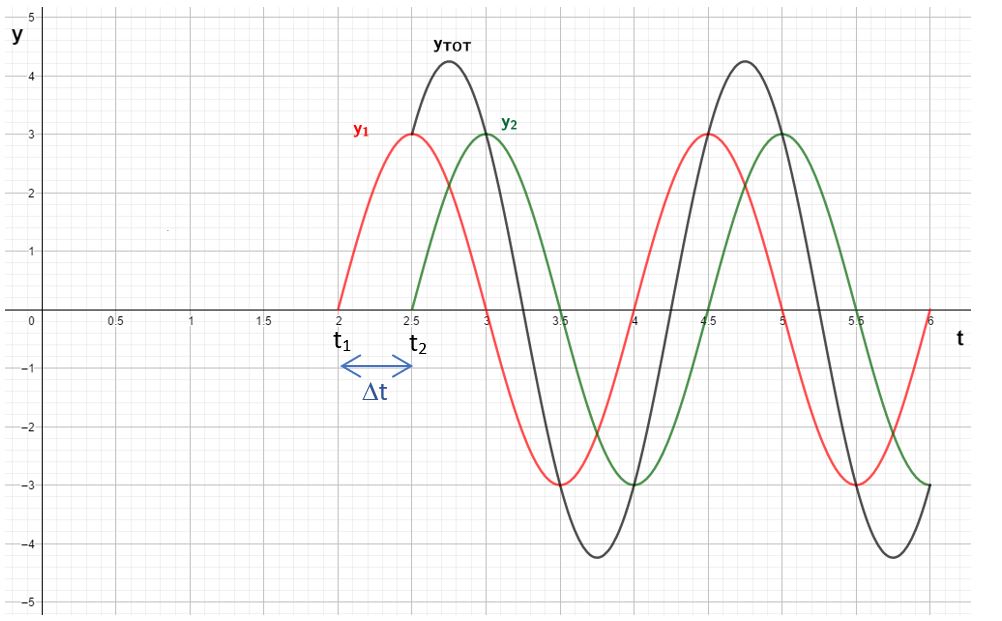
Puisque les ondes se baladent à vitesse constante, on peut définir leurs temps de parcours jusqu’au point P par:
\(t_{1}=\frac{d_{1}}{c}\)
\(t_{2}=\frac{d_{2}}{c}\)
Puisque \(d_{2}>d_{1}\), alors: \(t_{2}>t_{1}\) et le retard est donc défini par: \(\Delta t=t_{2}-t_{1}\)

Si le retard est un nombre entier de périodes, ça donne quoi?

Imaginons que le retard soit exactement égal à une période. Dans ce cas, le point P effectue une oscillation complète sous l’influence de la première source. Puis, lorsque la deuxième crête émise par \(S_{1}\) lui parvient, exactement à cet instant, arrive également la première crête en provenance de la deuxième source. On se retrouve donc avec deux crêtes qui se superposent exactement. Le point P vibre alors avec une amplitude double à chacune des sources. On parle d’interférence constructive.

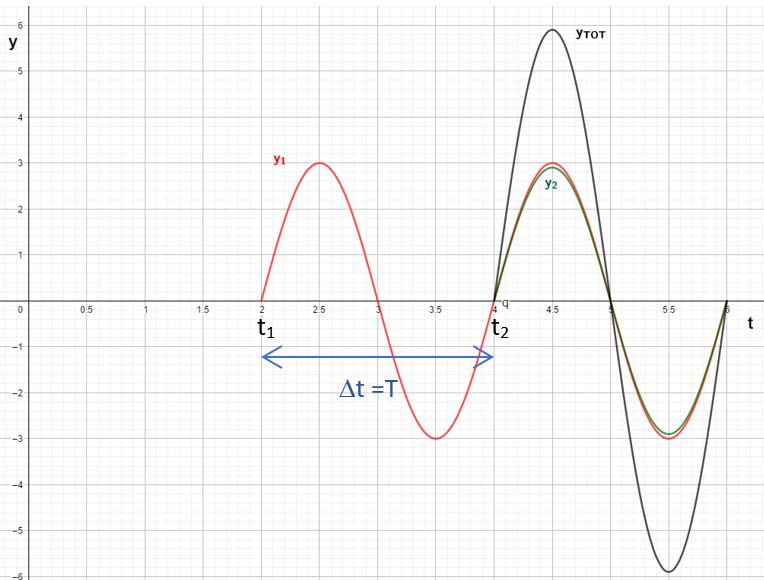
On devine facilement qu’il en sera de même si le retard vaut 2, 3 ou un nombre entier de périodes.
On obtient donc: Interférence constructive si \(\Delta t = kT\).

Et point de vue différence de marche, ça donne quoi?

Par définition, une onde parcourt une longueur d’onde \(\lambda \) en une période \(T\). On écrit donc: \(\lambda = c.T\) où c est la célérité de l’onde.

Tu as reconnu la formule du MRU? Comme l’onde avance à vitesse constante, on peut dire que \(\Delta x = v.\Delta t\)

On ajoutera donc:
interférence constructive si \(\Delta t = kT\) ou si \(\delta = k\lambda\)

Et si le retard est un nombre impair de demi-périodes, ça donne quoi?

Imaginons que le retard soit exactement égal à une demi-période. Dans ce cas, le point P effectue une demi-oscillation sous l’influence de la première source. Puis, lorsque le creux émis par \(S_{1}\) lui parvient, exactement à cet instant, arrive également la première crête en provenance de la deuxième source. On se retrouve donc avec une crête et un creux qui se superposent exactement. Le point P ne vibre plus. On parle d’interférence destructive.

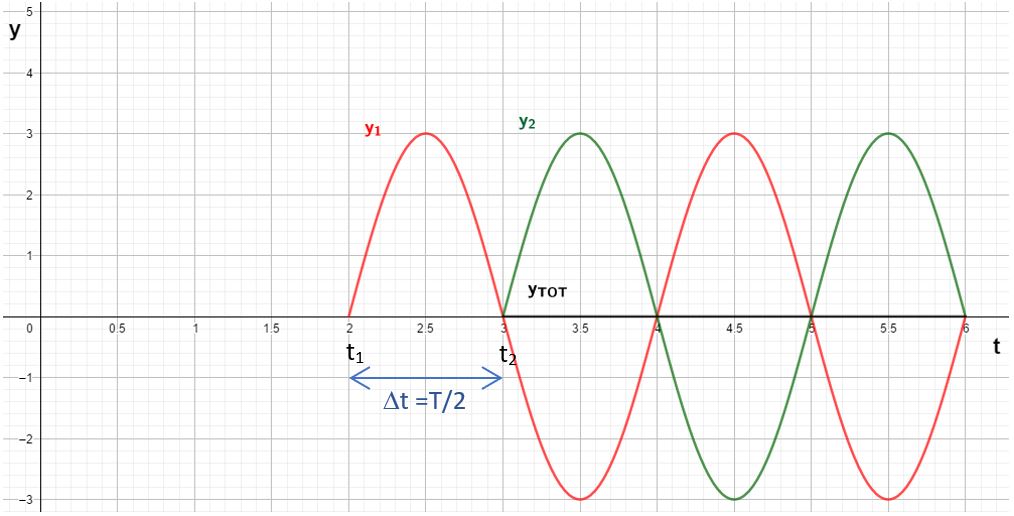
On devine facilement qu’il en sera de même si le retard vaut 3, 5 … ou un nombre impair de demi-périodes. En effet, un nombre pair de demi-périodes revient à un nombre entier de périodes. Vas relire le point précédent dans ce cas!
On obtient donc: Interférence destructive si \(\Delta t = (2k+1)\frac{T}{2}\).

Et point de vue différence de marche, ça donne quoi?

On a toujours la définition: \(\lambda = c.T\)
Une onde parcourt alors une demi longueur d’onde en une demi-période. On ajoutera donc:
interférence destructive si \(\Delta t = (2k+1)\frac{T}{2}\) ou si \(\delta = (2k+1)\frac{\lambda}{2}\)

III. Le déphasage \(\Delta \Phi\)

Observons le monde depuis le point P et regardons ce que les ondes nous amènent! Prenons les choses dans l’autre sens et commençons par étudier les interférences destructives.

Si le retard vaut une demi-période, la première source nous amène déjà un creux pendant que la seconde nous amène seulement sa première crête. Si on devait imaginer l’élongation du point P sous l’influence de chacune des deux ondes, on devrait dessiner ceci:

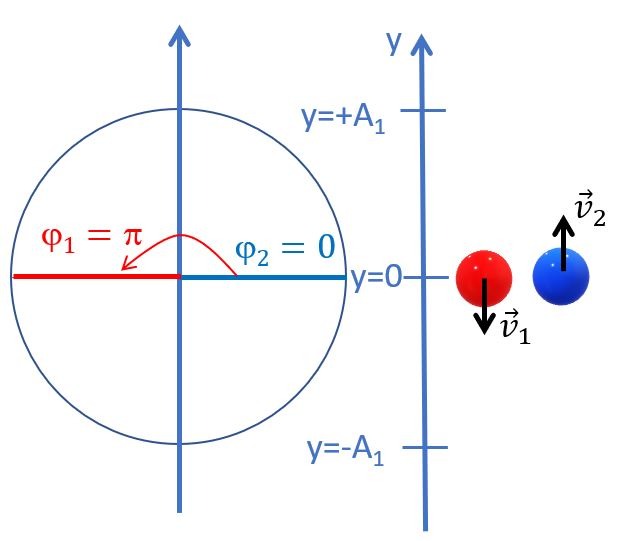
La première onde a une avance d’un demi cercle trigonométrique. Le déphasage entre les deux ondes vaut donc \(\Delta \Phi= |\phi_{2} – \phi_{1}| = \pi\).

Résumons pour les interférences destructives:

• Le retard d’une onde par rapport à l’autre est un nombre impair de demi-périodes: \(\Delta t = (2k+1)\frac{T}{2}\)
• Pour ce faire, une onde a dû parcourir un nombre impair de demi-longueurs d’onde en plus que l’autre: \(\delta = (2k+1)\frac{\lambda}{2}\)
• Vu autrement encore, le point P a déjà fait un nombre impair de demi-tours du cercle trigonométrique sous l’influence de la première onde, quand la seconde débarque: \(\Delta \Phi= (2k+1)\pi\)

Transposons pour les interférences constructives:

• Le retard d’une onde par rapport à l’autre est un nombre entier de périodes: \(\Delta t = kT\)
• Pour ce faire, une onde a dû parcourir un nombre entier de longueurs d’onde en plus que l’autre: \(\delta = k\lambda\)
• Vu autrement encore, le point P a déjà fait un nombre entier de tours complets du cercle trigonométrique sous l’influence de la première onde, quand la seconde débarque: \(\Delta \Phi= k*2\pi = 2k\pi\)

IV. CONCLUSION

Retenons qu’en une période (T):

• une onde parcourt une longueur d’onde (\(\lambda\))
• un point P fait un tour complet du cercle trigonométrique ( \(2\pi \))

Ayant ceci en tête, on pourra facilement se lancer à l’assaut de l’étude des couches minces, dans un prochain article! N’hésitez pas à me faire une critique constructive de mon travail dans l’espace « commentaires » ci-dessous ou tout simplement à liker si cet article vous a appris quelque chose. Merci!
A bientôt!