On parle beaucoup d’énergie potentielle dans l’enseignement secondaire, mais au final, cette notion n’est jamais claire. Dans quel cas se transforme-t-elle en énergie cinétique ? Qui possède vraiment cette énergie potentielle ? Alors, maintenant que vous avez acquis une maturité suffisante, et avant de nous lancer dans la comparaison entre l’énergie potentielle gravifique et l’énergie potentielle électrique, reprenons depuis le début ! Courage, ce n’est qu’un mauvais moment à passer… Par contre, il est quand même préférable que vous fassiez un petit détour par ici si la notion de travail mécanique n’est pas claire pour vous.

Première définition de l’énergie potentielle par rapport aux forces extérieures

Définition : On définit l’énergie potentielle comme l’énergie attribuable aux positions relatives de deux ou plusieurs particules en interaction.

 

Exemple : Une pomme placée à une certaine altitude par rapport au sol.

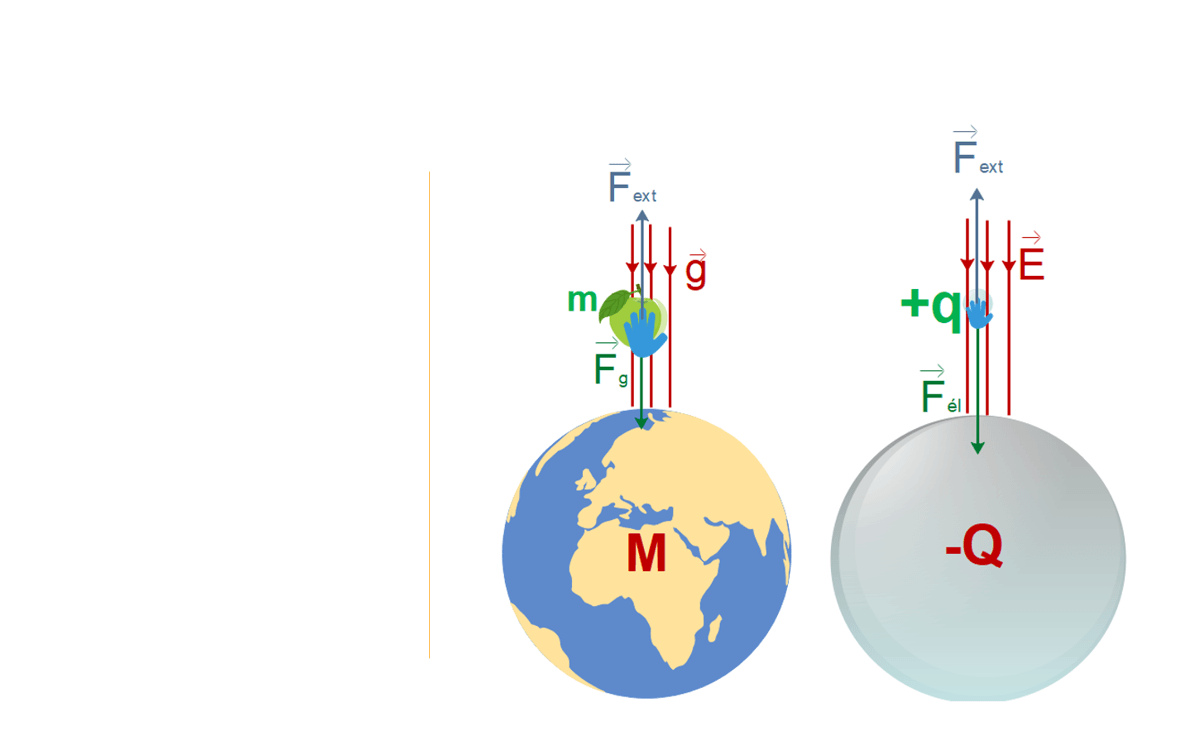
L’état d’équilibre est la position stable de la pomme au sol. Pour amener la pomme à une certaine altitude, il faut qu’un agent extérieur, càd une force extérieure au système Terre-Pomme \( (\overrightarrow{F}_{ext}) \) effectue un travail contre la force gravifique. Ce travail, noté \( W_{ext} \) est alors stocké par le système Terre-pomme sous forme d’énergie potentielle gravitationnelle notée \( U_{g} \)
.

Rmq : Nous parlons presque toujours de l’énergie potentielle de la pomme parce que nous ne voyons que la pomme se déplacer quand on la lâche. On ne perçoit pas le mouvement de la Terre qui existe pourtant (bien qu’imperceptible) d’après la loi des actions réciproques : si la Terre attire la pomme, la pomme attire également la Terre.

 

Donc, le travail de l’agent extérieur fournit l’énergie potentielle gravifique U_g au système Terre-pomme. Si la force extérieure (\(\overrightarrow{F}_{ext}\)) compense exactement la force gravifique que la Terre exerce sur la pomme (\(\overrightarrow{F}_{T/P}\)); le déplacement se fait à vitesse constante \( (\sum F=0) \). Dès lors, il n’y a pas de variation d’énergie cinétique et l’entièreté du travail extérieur sert à augmenter l’énergie potentielle du système, on peut donc écrire :

\(W_{ext}=\Delta U = U_{f}-U_{i}\)

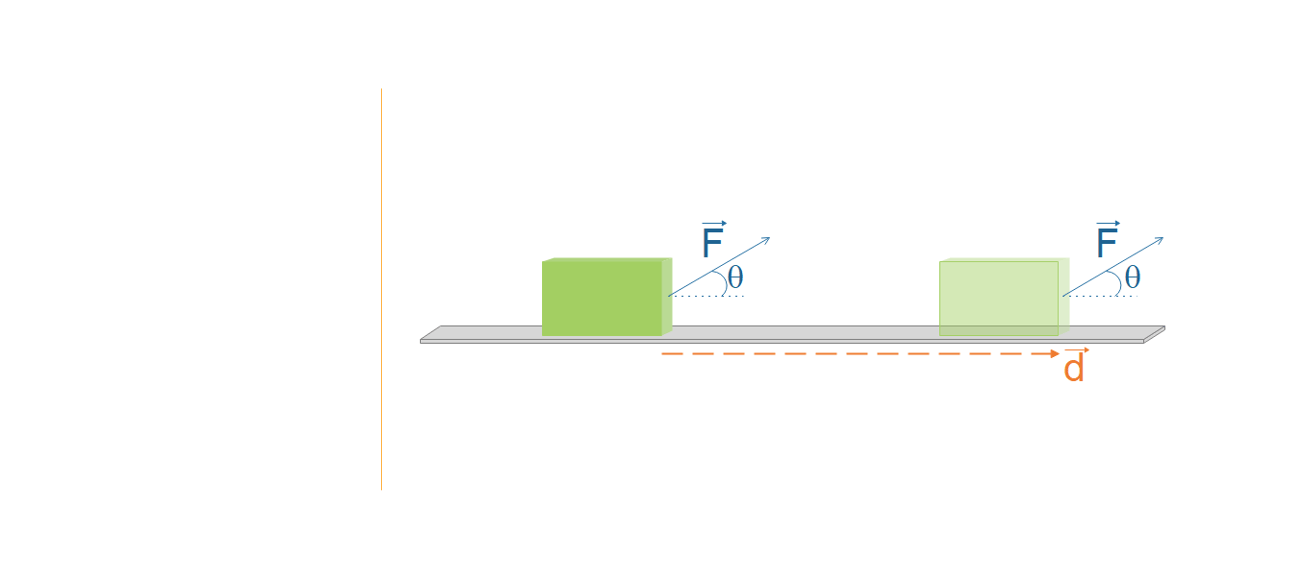
Si le travail extérieur est moteur \( (W > 0\) càd que la force extérieure \(\overrightarrow{F}_{ext}\) agit dans le sens du déplacement \(\overrightarrow{d}\)), l’énergie potentielle est augmentée (car \( U_{f}>U_{i} \)); tandis qu’elle est diminuée si le travail extérieur est résistif \( (W < 0) \).

Dans la plupart des cas, on définit l’énergie potentielle gravifique nulle au niveau du sol : \(U_{i}=0.\) Ce qui amène \(W_{ext}=\Delta U = U_{f}\). Nous pouvons donc proposer une nouvelle définition à l’énergie potentielle gravifique :

Définition: L’énergie potentielle gravifique d’un système est le travail extérieur nécessaire pour amener les particules à vitesse constante, de la configuration U=0 à une position donnée.

 

Toutefois, cette définition est restrictive parce qu’elle fait intervenir la notion de force extérieure et qu’elle impose un déplacement à vitesse constante.

Analysons la situation encore un peu plus en détail en étudiant les forces internes conservatives.

 

Les forces internes conservatives

Vous avez vu dans vos cours du secondaire que le travail effectué par la force gravifique sur une masse ne dépend pas du chemin parcouru mais uniquement des positions initiales et finales. What?
Ce n’est pas très compliqué à comprendre, vous savez que le travail de la force gravifique est donné par:

\(W_{g} = \; -mg.(y_{ f } \; -y_{ i }) \tag 1\\ \)

Considérons l’élévation d’une particule depuis l’altitude initiale \(y_{i}\) (point A) jusqu’à l’altitude finale \(y_{f}\) (point B), le travail résistif de la force pesanteur durant l’élévation ne dépend que des altitudes \(y_{i}\) et \(y_{f}\), pas du chemin parcouru. C’est logique: que la particule emprunte le chemin 1 ou le chemin 2 ; elle gagne exactement la même énergie potentielle gravifique qui ne dépend que de la différence d’altitude \( (\Delta y) \), le travail effectué est donc le même dans les deux cas.

 

 

 

 

 

 

Remarquez par ailleurs, que l’expression (1) implique que, sur une boucle fermée (\( y_{ f } = y_{ i } \)) le travail global de la force gravifique est nul.

Dès lors, on dira de la force pesanteur qu’elle est conservative.

A l’inverse, si on étudiait le travail de la force de frottement, le résultat serait différent en fonction du chemin emprunté. En effet, le chemin 2 étant plus long que le chemin 1, le travail de la force de frottement (\( W_{F_{ f }} = \; -F_{ f }.d \)) serait plus important. La force de frottement n’est donc pas une force conservative.

 

Conclusion: le travail effectué par une force conservative est indépendant du chemin parcouru et est nul sur une trajectoire fermée !

En réalité, l’énergie potentielle ne peut être définie que pour des forces conservatives.

Reprenons notre pomme élevée à vitesse constante. Etant donné que la somme des forces est nulle, la somme des travaux doit l’être également. Le travail total effectué sur la pomme, d’une part par la force extérieure \( W_{ ext}\), càd la main, et d’autre part par la force gravifique interne ( \( W_{g} \)) est nul. On écrira :

\( W_{g} + W_{ext}=0 \;\Leftrightarrow \;W_{g} =\: -W_{ext} \)

 

Or, comme on sait que la force extérieure communique une énergie potentielle gravifique à la particule sur laquelle elle agit (\( W_{ext}=\Delta U \)), on notera finalement :

\( W_{g} = \; – \Delta U =\; – (U_{f}-U_{i}) \)

 

Cette relation est toujours valable, quelle que soit la vitesse ou les forces agissant sur la particule. OUF ! Tout ça pour ça ! Eh oui….

Par contre, prenez le temps d’enregistrer une chose importante en observant cette relation que je note à nouveau :

\( W_{g} = \; – \Delta U =\; – (U_{f}-U_{i}) \)

Si le travail de la force gravifique (ou force interne conservative) est résistif (i.e.: \( \overrightarrow{F}_{g} \) est opposée au déplacement \(\overrightarrow{d} \Leftrightarrow W<0 \) et donc \(\Delta U >0 \) ), alors l’énergie potentielle augmente.
Si le travail de la force gravifique (ou force interne conservative) est moteur ((i.e.: \( \overrightarrow{F}_{g} \) est dans le sens du déplacement \(\overrightarrow{d} \Leftrightarrow W>0 \) et donc \(\Delta U <0 \) ), alors l’énergie potentielle diminue.
Est-ce toujours vrai ? Terminons cette partie en prenant un autre exemple de force conservative, celle exercée par un ressort sur une masse qui lui est attachée.

Situation 1 : Le système est à l’équilibre et ne possède pas d’énergie potentielle élastique U=0.

Situation 2 : Alors qu’une force extérieure déplace la masse vers la gauche, le ressort exerce sa force élastique de rappel vers la droite. Le travail de la force élastique interne (\( W_{k} \)) est donc résistif et le système acquiert bien une énergie potentielle élastique U (\( \scriptsize W_{k} = \; – \Delta U <0 \rightarrow \Delta U>0 \rightarrow U_{f}>U_{i} \))

Situation 3 : Pendant le retour de la masse vers le point d’équilibre, la force élastique effectue un travail moteur et le système perd son énergie potentielle élastique U qu’il convertit en énergie cinétique.
 
(\( \scriptsize W_{k} = \; – \Delta U >0 \rightarrow \Delta U<0 \rightarrow U_{f} < U_{i} \)) \( \\ \) Situation 4 : la masse dépasse sa position d’équilibre et comprime le ressort qui exerce une force de rappel vers la gauche, le travail élastique (\( W_{k} \)) est donc résistif et le système acquiert une énergie potentielle élastique. CQFD !  

L’énergie potentielle électrique et le potentiel électrique

Maintenant que la notion d’énergie potentielle est acquise en mécanique, nous allons pouvoir la transposer au monde électrique.

Vous savez que la force gravifique est conservative et que, exprimée dans son détail, elle a la forme suivante :

\(F_{g} = G.{M.m \over d^2} \)

Par ailleurs, vos cours du secondaire ont dû vous apprendre que la force électrique est exactement de la même forme :

\(F_{él} = k.{Q.q \over d^2} = {1 \over 4\pi\epsilon_{0}}.{q.Q \over r^2} \)

Dès lors, par transposition, vous comprendrez que la force électrique est elle aussi conservative.

 

Faisons donc une analogie entre le monde gravifique et le monde électrique.

Nous savons déjà qu’au cours de l’ascension de la pomme sous l’effet d’une force extérieure, le travail de la force gravifique (interne conservative) est négatif et que l’énergie potentielle gravifique du système augmente.

De façon analogue, au cours de l’ascension de la petite charge q sous l’effet d’une force extérieure, le travail de la force électrique (interne conservative) est négatif et donc l’énergie potentielle électrique du système augmente.

Le travail de la force gravifique nous a permis d’évaluer l’énergie potentielle gravifique; le travail de la force électrique va nous permettre d’évaluer l’énergie potentielle électrique. Si on note un déplacement infinitésimal \(\overrightarrow{dr}\), on peut reprendre la définition du travail :

\[W_{E}= \int {\overrightarrow{F_{E}}.\overrightarrow{dr}}=\int {{1 \over 4\pi\epsilon_{0}}.{q.Q \over r^2}.dr.cos(180)}\]

En effet, on sait déjà que l’intensité de la force électrique (\(F_{él} \)) est donnée par \({1 \over 4\pi\epsilon_{0}}.{q.Q \over r^2} \) avec \({1 \over 4\pi\epsilon_{0}} \) la constante électrique et avec les charges q et Q prises en valeur absolue. On voit par ailleurs que le déplacement qui se fait vers le haut est opposé à la force électrique et que l’angle à considérer est donc de 180°.

Résolvons cette intégrale, nous obtenons :
\[W_{E}= \:-{q.Q \over 4\pi\epsilon_{0}}\int {{1 \over r^2}.dr}=\:-{q.Q \over 4\pi\epsilon_{0}}\int {{r^{-2}}.dr}=\:-{q.Q \over 4\pi\epsilon_{0}}(r^{-1})={1 \over 4\pi\epsilon_{0}}.{q.Q \over r} \]

Finalement, nous obtenons la définition de l’énergie potentielle électrique (exprimée en [JOULE]) :
\[U_{E}= \:{1 \over 4\pi\epsilon_{0}}.{q.Q \over r} \]

Remarquons que nous aurions pu faire le même raisonnement en rapprochant une charge positive +q d’une charge influente +Q.

Le problème de cette expression est qu’elle dépend de la valeur de la petite charge positive sous influence (+q) qui est éloignée de la grande charge négative influente (-Q).

Définissons alors une grandeur qui ne dépend pas de cette petite charge sous influence, soit : \({U_{E} \over q} \). Cette valeur est donc exprimée en Joule par Coulomb, et nous l’appellerons le potentiel électrique V.

Nous avons donc :\[V={U_{E} \over q} \]

Les unités du potentiel électrique sont les suivantes : \([V]= \left[\frac{J}{C}\right] \) . En effet, les Physiciens (qui sont des gens biens) ont décidé de rendre hommage à Alessandro Volta en appelant le ‘Joule par Coulomb’ le VOLT.

 

Retenons donc que le potentiel électrique est l’énergie électrique qu’une charge influente est capable de donner à une charge hypothétique de 1 coulomb en un point donné.

 

Différence de potentiel et lignes de champ électrique

Vos cours du secondaire vous ont appris à comparer les deux écritures suivantes :
\[ \overrightarrow{F_{g}} = m.\overrightarrow{g} \]
et
\[\overrightarrow{F_{él}}=q.\overrightarrow{E}\]

 

Lorsqu’une masse (scalaire +) est placée en un point auquel règne un champ gravifique \(\overrightarrow{g}\), elle subit une force gravifique \(\overrightarrow{F_{g}}\) qui possède même sens et même direction que ce champ. (Si cette notion n’est pas claire, allez revoir les « 7 outils mathématiques indispensables pour réussir en physique »).

De façon équivalente, lorsqu’une charge positive (scalaire +) est placée en un point auquel règne un champ électrique \(\overrightarrow{E}\), elle subit une force électrique \(\overrightarrow{F_{él}}\) qui possède même direction et même sens que le champ. Si la charge placée dans le champ est négative, alors la force électrique qui en résultera possèdera même direction mais sera de sens opposé au champ électrique.

Sur cette représentation, le champ gravifique \( \overrightarrow{g} \) est généré par M, on parlera de la masse influente ; tandis que le grand-père (de petite masse m) est placé dans ce champ ; il subit donc son influence : il est soumis à une force gravifique \( \overrightarrow{F_{g}} \). On dira donc que m est la masse sous influence.

De façon analogue, la charge Q est la charge influente, elle génère autour d’elle un champ électrique \( \overrightarrow{E} \). Dès lors, si on place une petite charge q dans ce champ, cette charge ressentira l’influence du champ électrique et sera donc soumise à une force électrique \( \overrightarrow{F_{E}} \). On dira que la petite charge q est la charge sous influence.

 

Une masse m placée à une altitude y par rapport au sol (y=0) possède une énergie potentielle gravifique \(U_{g}=m.g.y\)

Par analogie, une charge q placée à une distance r par rapport à la surface de la charge influente (r=0) possède une énergie potentielle électrique \(U_{E}=q.E.r\). En effet, dans cette relation, le champ gravifique g devient le champ électrique E, la masse sous influence m, devient la charge sous influence q et l’altitude y est remplacée par la distance r.

 

Et donc, comme \(V={U_{E} \over q} \), on a : \(V={q.E.r \over q}=E.r \)

 

On retrouve la même conclusion qu’au point précédent, à savoir que le potentiel électrique V, ne dépend donc que de la charge influente (qui fixe la valeur de E) et de la position par rapport à cette charge (qui fixe les valeurs de E et de r). Le potentiel électrique est donc indépendant de la petite charge q qui est soumise à l’influence électrique.
\[V=E.r \Leftrightarrow E={V\over r} \]
Cette relation nous montre, par ailleurs, que le champ électrique qui s’exprime habituellement en [N/C] quand on le considère comme responsable d’une force sur une charge (\(\overrightarrow{F_{él}}=q.\overrightarrow{E}\)) peut également s’exprimer en [V/m] ou encore en [J/C.m] quand on le considère comme responsable d’une énergie apportée à une charge placée à une distance (r) donnée.

 

Important à comprendre :

Tout comme une masse qui s’élève à la surface de la Terre, se déplace contre les lignes de champ gravifique, voit son énergie potentielle gravifique augmenter, une charge (+) qui se déplace contre les lignes de champ électrique, voit son énergie potentielle électrique augmenter.

Tout comme une masse a une tendance naturelle à suivre les lignes de champ gravifique et à perdre son énergie potentielle gravifique. On dira donc qu’une charge positive a une tendance naturelle à suivre les lignes de champ électrique et à perdre son énergie potentielle électrique. Dit autrement encore, une charge électrique positive a tendance à se déplacer vers les potentiels plus faibles.

Allons plus loin :

Les charges électriques négatives placées dans un champ électrique se déplacent en sens contraire au champ électrique. Perdent-elles ou gagnent-elles de l’énergie potentielle électrique ?

 

Pour le savoir, il est bon de reprendre, une fois de plus, l’analogie avec le système pomme-Terre. Naturellement, sous l’influence de l’attraction gravitationnelle, la pomme a tendance à se rapprocher de la Terre et donc, à perdre son énergie potentielle gravifique.

Si on considère une charge influente Q positive. Vos cours de secondaire vous ont appris que la grande charge Q positive génère un champ sortant, càd dirigé vers l’extérieur et donc, les lignes de champ électrique sont dirigées vers l’extérieur. Une petite charge q négative, placée dans ce champ, se déplacera naturellement en sens opposé au champ, càd vers la grande charge Q positive (c’est l’attraction électrique entre ces deux charges qui est à l’œuvre). Tout comme la pomme ne possède plus d’énergie potentielle gravifique quand elle est tombée sur le sol, la charge q ne possédera plus d’énergie potentielle électrique quand elle sera collée à la charge influente Q. Une charge q négative a donc tendance à perdre son énergie potentielle électrique et à se déplacer vers les champs électriques croissants (E est le plus intense près de la charge +Q).

Qu’en est-il d’une charge positive ? Une charge positive se déplacera dans le sens des lignes de champ, càd vers l’extérieur, c’est la force répulsive qui est à l’œuvre. Tout comme un ressort comprimé, c’est quand cette petite charge positive q est collée à la grande charge positive +Q que la force répulsive est la plus grande et donc, que l’énergie potentielle électrique est maximale. Dès lors, une charge positive q qui a tendance à s’éloigner de +Q a donc tendance à perdre son énergie potentielle électrique et à se déplacer vers des champs électriques décroissants.

Conclusion : Dans un champ électrique \(\overrightarrow{E}\) extérieur, toutes les charges (+ ou -) ont tendance à subir une diminution d’énergie potentielle électrique: les charges positives, en se déplaçant vers des champs électriques décroissants (ou vers des potentiels électriques décroissants puisque \(E={V\over r} \)), tandis que les charges négatives perdront leur énergie potentielle électrique en se déplaçant vers des champs électriques croissants (ou vers des potentiels électriques croissants) .

 

 

L’essentiel de cet abominable article !

Nous avons vu que nous pouvons définir l’énergie potentielle (gravifique ou électrique) en considérant une force extérieure qui doit contrer une force interne conservative (gravifique ou électrique) pour déplacer une masse ou une charge.

Dans ce cas, si le travail de la force extérieure est positif \(\Rightarrow\) l’énergie potentielle (gravifique ou électrique) augmente ( \(W_{ext}=\Delta U = U_{f} \) ). Tandis que si le travail de la force extérieure est négatif \(\Rightarrow\) l’énergie potentielle (gravifique ou électrique) diminue.

 

Nous pouvons également regarder les choses de l’intérieur ; dans ce cas :

Si le travail de la force interne (gravifique ou électrique) est positif \(\Rightarrow\) l’énergie potentielle (gravifique ou électrique) diminue ( \( W_{c} = \; – \Delta U =\; – (U_{f}-U_{i}) \) ). Tandis que si le travail de la force interne est négatif \(\Rightarrow\) l’énergie potentielle (gravifique ou électrique) augmente.

 

Une masse se déplace toujours dans le sens des lignes de champ gravifique et elle perd donc naturellement son énergie potentielle gravifique (sans l’intervention d’un agent extérieur).

Une charge positive se déplace toujours dans le sens des lignes de champ électrique et elle perd donc naturellement son énergie potentielle électrique (sans l’intervention d’un agent extérieur). Une charge positive se déplace donc naturellement vers des potentiels plus faibles.

Une charge négative se déplace toujours dans le sens opposé des lignes de champ électrique, ce faisant, elle perd également naturellement son énergie potentielle électrique (sans l’intervention d’un agent extérieur). Une charge négative se déplace donc naturellement vers des potentiels plus forts.

Voilà, bravo! Tu es arrivé au bout de cet article! Si tu as des questions, n’hésite pas à les poser en postant des commentaires ci-dessous!