Recevez gratuitement
mon livret!
Bonjour à toutes et à tous,
\(\\\)
Aujourd’hui, vous allez apprendre à comprendre la construction géométrique du vecteur vitesse sur une chronophotographie. Si vous essayez de tout retenir par cœur, vous allez vite être largué, dégouté et fâché (et si c’est pas maintenant, ce sera avec la construction du vecteur accélération)… A l’inverse, si vous vous efforcez de comprendre chaque détail de la construction, vous allez être hyper performant! Et même, je crois que vous pourriez y prendre un certain plaisir! Si si, je vous assure!
Allez, on essaie!
\(\\\)
\(\\\)
Aujourd’hui, vous allez apprendre à comprendre la construction géométrique du vecteur vitesse sur une chronophotographie. Si vous essayez de tout retenir par cœur, vous allez vite être largué, dégouté et fâché (et si c’est pas maintenant, ce sera avec la construction du vecteur accélération)… A l’inverse, si vous vous efforcez de comprendre chaque détail de la construction, vous allez être hyper performant! Et même, je crois que vous pourriez y prendre un certain plaisir! Si si, je vous assure!
Allez, on essaie!
\(\\\)
Qu’est-ce qu’une chronophotographie?
C’est une succession de photographies prises à intervalles de temps réguliers et superposées les unes aux autres. Concrètement, ça donne quelque chose comme ceci:
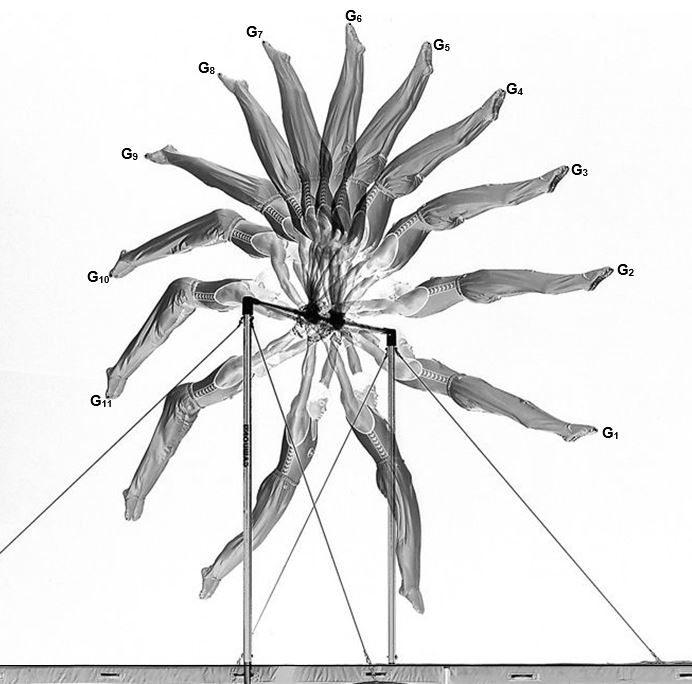
Les annotations sur le bout des pieds permet de voir que le mouvement se fait dans le sens anti-horloger. \(\\\)
L’intervalle de temps compris entre deux positions successives, s’appelle la base de temps et se note \(\tau\). C’est un élément essentiel à l’interprétation de la photo, mais nous en reparlerons dans un instant.
Essayons de construire le vecteur vitesse à la position notée \(G_{6}\).
1ère étape: écrire la définition et la comprendre!
Bon oui, c’est peut-être bête, mais c’est important. C’est quoi encore, la définition du vecteur vitesse instantanée?
\begin{equation}
\ \overrightarrow{v} = \lim\limits_{\Delta t \rightarrow 0} \frac{\Delta \overrightarrow{r}}{\Delta t_{ }}
\end{equation}
Et je sais ce que vous vous dites: « Ah ouais, d’accord … et, on en fait quoi de cette définition??? »
Et bien, on la décortique! A quoi fait-elle appel? Au vecteur déplacement et à l’intervalle de temps.
\(\\\)
Sauf qu’il y a ce petit truc en plus: « \(\lim\limits_{\Delta t \rightarrow 0}\) ».
\(\\\)
Bon, okay, c’est une notion théorique de mathématicien … ouais, je sais, ça ne donne pas envie …
Mais bon, concrètement, ça donne quoi? Parce que la théorie, c’est bien, mais la pratique, c’est mieux! Un intervalle de temps infiniment petit les amis, c’est impossible concrètement parlant! Il nous faut donc nous adapter et trouver le plus petit intervalle de temps possible d’après les données que nous avons en notre possession. OUCH! Allons voir les informations sur la chronophoto!
2ème étape: relever les données de la chronophotographie
Il y a trois éléments essentiels:
- Le sens du mouvement (de bas en haut, de la gauche vers la droite…)
- La base de temps
- L’échelle de la figure
Nous avons déjà repéré le sens du mouvement. La base de temps est de 150 ms. ATTENTION! Soyez certains de lire correctement les unités! En physique, la moitié des réponses se trouve dans les unités! \(\\\)Comment lit-on « ms »? \(\\\)
J’entends parfois des élèves dire « èm-és » …. ou, pire plus grave, « mètre-seconde »! Et là, on se rend compte une fois de plus que le fameux kilomètre-heure dont je vous ai parlé précédemment refait surface! Apprenez à maitriser les outils que vous utilisez, c’est important.
\(\\\)Que lisez-vous? Une base de temps! \(\\\)
On parle donc bien d’un TEMPS! et un temps, s’exprime (dans le système international) en seconde! « ms », ce n’est donc pas plus compliqué que « mm » pour exprimer des petites distances ou que « mg » pour exprimer des petites masses. « ms » signifie donc tout simplement « milliseconde », càd (écoutez le terme) millième de seconde.
Donc, un intervalle de temps de 150 millièmes de seconde sépare deux positions: \(\tau=0,150 s\). \(\\\)
Il nous reste à relever l’échelle de la figure qui est la suivante: \( 1 \ cm \ papier \leftrightarrow 0,25 m \) \(\\\)
Ici encore, il est important de bien comprendre de quoi on parle: dès que je mesure 1cm sur mon papier, il représente en réalité 25 cm!
3ème étape: appliquer la définition
Nous voulons caractériser la vitesse au point \(G_{6}\). Pour ce faire, la définition (1) nous demande de prélever un vecteur déplacement sur un intervalle de temps le plus petit possible. Dans un premier temps, on pourrait penser que cet intervalle de temps est de 150 ms, mais on a alors un problème.
\(\\\) Si on considère le vecteur déplacement dont l’origine est le point \(G_{5}\) et l’extrémité le point \(G_{6}\), appelons-le \(« \Delta \overrightarrow{r}_{56} »\), il s’effectue en 150ms. Toutefois le rapport \(\frac{\Delta \overrightarrow{r}_{56}}{\Delta t_{ }}\) correspondra à la vitesse que le gymnaste possédait avant le point \(G_{6}\)!
\(\\\) De façon similaire, le vecteur déplacement dont l’origine serait le point \(G_{6}\) et l’extrémité le point \(G_{7}\), appelons-le \(« \Delta \overrightarrow{r}_{67} »\), conduirait au rapport \(\frac{\Delta \overrightarrow{r}_{67}}{\Delta t_{ }}\) qui correspondrait à la vitesse que le gymnaste possède après le point \(G_{6}\)!
\(\\\)
La façon la plus précise que nous offre cette chronophotographie pour déterminer la vitesse du gymnaste au point \(G_{6}\) consiste alors à prendre le vecteur déplacement de part et d’autre de ce point, càd le vecteur dont l’origine est le point \(G_{5}\) et l’extrémité le point \(G_{7}\). Par convention, nous écrirons ce vecteur déplacement \(« \Delta \overrightarrow{r_{6}} »\), càd le vecteur variation de position de part et d’autre du point 6. Ce changement de position a lieu en deux intervalles de temps \(\tau \). On aura donc: \(\Delta t = 2.\tau \). C’est fondamental de bien le comprendre!
\(\\\)Choisissons un référentiel (X,Y) et traçons le vecteur \(\Delta \overrightarrow{r_{6}}\). Etant donné qu’il s’agit du premier exercice, nous traçons également les vecteurs \(\overrightarrow{r}_{5}\) et \(\overrightarrow{r}_{7}\). En réalité, ils sont inutiles puisque, quel que soit le référentiel choisi, le vecteur déplacement ira toujours de la première position à la seconde. (Pour rappel).
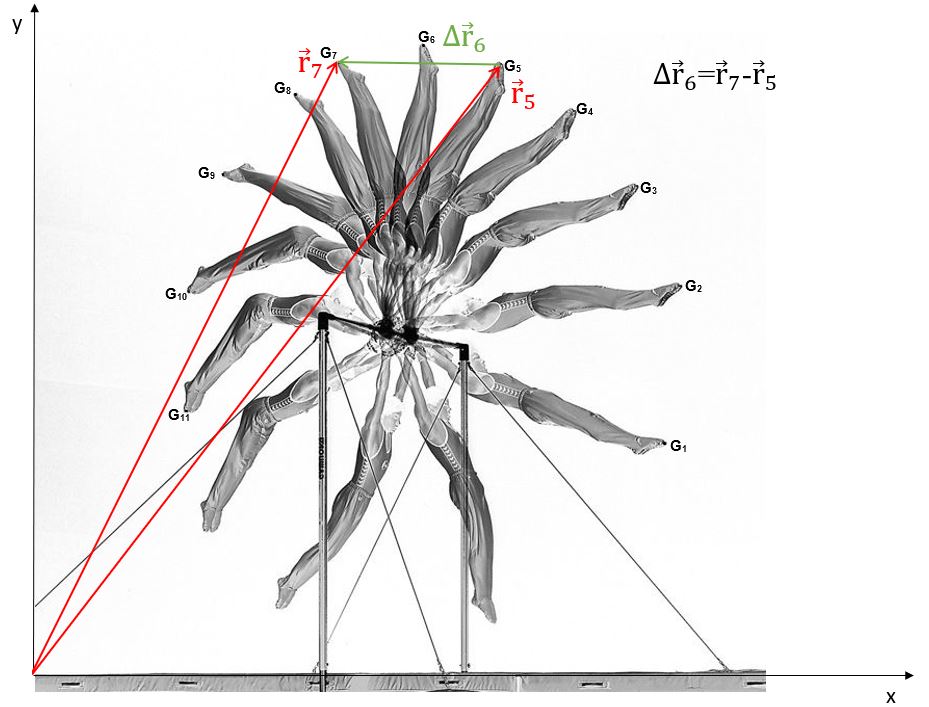
Le vecteur déplacement mesure exactement 4 cm sur papier. Toutefois, l’existence d’une échelle va nous obliger à faire des transferts entre « papier » et « réalité ». Le plus simple est, je pense, de réaliser un tableau comme le suivant:\(\\\)
| Sur papier | En réalité |
|---|---|
| \( \lVert \Delta \overrightarrow{r_{6}}\lVert \) = 4 cm | \( \lVert \Delta \overrightarrow{r_{6}}\lVert \) = 100 cm = 1m |
| \(\Delta t\) = 2 \(\tau\) = 300 ms = 0,3 s | |
| \( \lVert\overrightarrow{v_{6}}\lVert = \lVert\Delta\overrightarrow{r_{6}}\lVert / \Delta t = 1/0,3 = 3,3 m/s\) | |
| Nous devons donc représenter sur papier un vecteur vitesse dont la norme est de 3,3 m/s. Pour ce faire, nous allons choisir une échelle: 1 cm papier \(\leftrightarrow\) 1 m/s Nous devons donc tracer un vecteur vitesse de 3,3 cm de longueur. |
4ème étape: tracer le vecteur vitesse sur papier
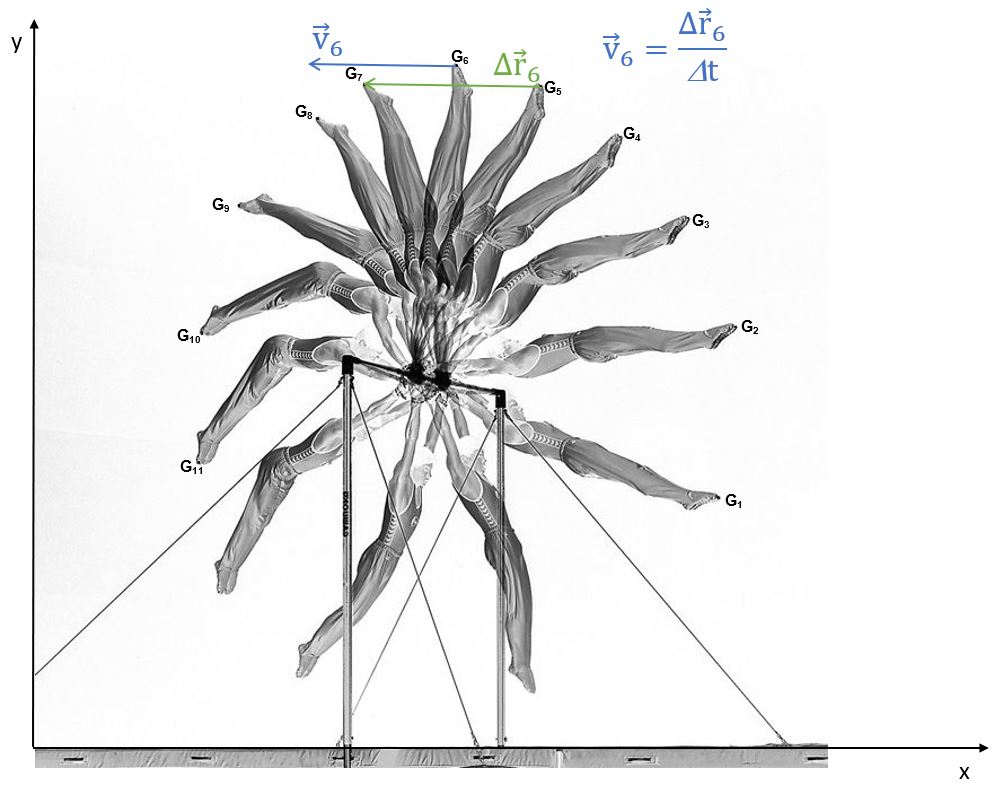
Nous connaissons maintenant la norme du vecteur vitesse au point \(G_{6}\) et nous savons qu’il a exactement la même direction et le même sens que le vecteur \(\Delta\overrightarrow{r_{6}}\) puisque \(\Delta t\) est un scalaire toujours positif. Il nous reste donc à dessiner ce vecteur dont le point d’application est \(G_{6}\).
\(\\\)
IL Y A UN TRUC: \( \ \) afin de savoir si votre vecteur est cohérent, souvenez-vous qu’un vecteur vitesse (instantanée) est TOUJOURS tangent à la trajectoire! Si votre vecteur coupe la trajectoire, vous avez fait une erreur, cherchez-la!
\(\\\)
\(\\\)
P.S.: Si cet article vous a plu, n’hésitez pas à vous abonner grâce à la fenêtre apparaissant tout en bas de cette page (sur fond bleu). Vous recevrez ainsi une notification e-mail pour chaque nouvel article publié. Sinon, laissez un pouce bleu ou un commentaire que je sache si mon travail vous est utile. Merci et à la prochaine!
Partager l'article:
administrator
À propos de l’auteur